Lecture 2 Bits Bytes Number systems Representation of

Lecture 2 Bits, Bytes & Number systems

Representation of Numbers q Different ways to say “how many”… q Human: decimal number system v v Radix-10 or base-10 Base-10 means that a digit can have one of ten possible values • 0 through 9. q Computer: binary number system v v v Radix-2 or base-2 Why binary? Each digit can have one of two values • 0 or 1

Bits and Bytes q A binary digit is a single numeral in a binary number. q Each 1 and 0 in the number below is a binary digit: 10010101 q The term “binary digit” is commonly called a “bit. ” q Eight bits grouped together is called a “byte. ”

Relationship between Decimal & Binary Background: q Number systems are positional q There are 10 symbols that represent decimal quantities q Multi-digit numbers are interpreted as in the following example q 79310 = 7 x 100 + 9 x 10 + 3 = 7 x 102 + 9 x 101 + 3 x 100 Remember that the position index starts from 0. q Each place value in a decimal number is a power of 10. q We can get a general form of this v ABCbase v A x (base)2 + B x (base)1 + C x (base) 0 Indicate positions

Relationship between Decimal & Binary q Binary numbers are represented using the digits 0 and 1. q Multi-digit numbers are interpreted as in the following example q 101112 = 1 x 24 + 0 x 2 3 + 1 x 2 2 + 1 x 2 1 + 1 x 2 0 = 1 x 16 + 0 x 8 + 1 x 4 + 1 x 2 + 1 x 1 q Each place value in a binary number is a power of 2.

Converting binary numbers to decimal Step 1: Starting with the 1’s place, write the binary place value over each digit in the binary number being converted. Step 2: Add up all of the place values that have a “ 1” in them. Interpret the binary number 101012 in decimal q TRY: Interpret the binary number 010101102 in decimal

Converting decimal numbers to binary q We have now learnt how to convert from binary to decimal v Using positional representation q But how about decimal to binary v Repeated division method • Simply keep dividing it by 2 and record the remainder • Repeat above step as many times as necessary until you get a quotient that can’ t be divided by 2 • Remainders give the binary digits, starting from the last remainder q Let’s look at some examples…

Converting decimal numbers to binary q Let’s convert decimal 23 to binary. Step 1: 23/2 = 11 remainder 1 Step 2: 11/2 = 5 remainder 1 Step 3: 5/2 = 2 remainder 1 Step 4: 2/2 = 1 remainder 0 q The last quotient “ 1” cannot be divided by 2 any more. So the process ends. The final binary number is read from the very end including the last quotient: 10111 q Try: Convert decimal 73, 96, 127, 128 to binary.

Hexadecimal q Computers use binary number system because of the electric voltage (high or low voltage) v Very difficult to express for large number representation q Hexadecimal to rescue v v Hexadecimal system is interface between human brain and computer brain 4 bits from binary are read together and represented using a single digit • Such 4 -bits are known as nibble • This gives a total of 16 different options q The hexadecimal number system is a Base-16 number system: v v There are 16 symbols that represent quantities: Represented by the symbols 0 -9 and A-F where the letters represent values: A=10, B=11, C=12, D=13, E=14, and F=15

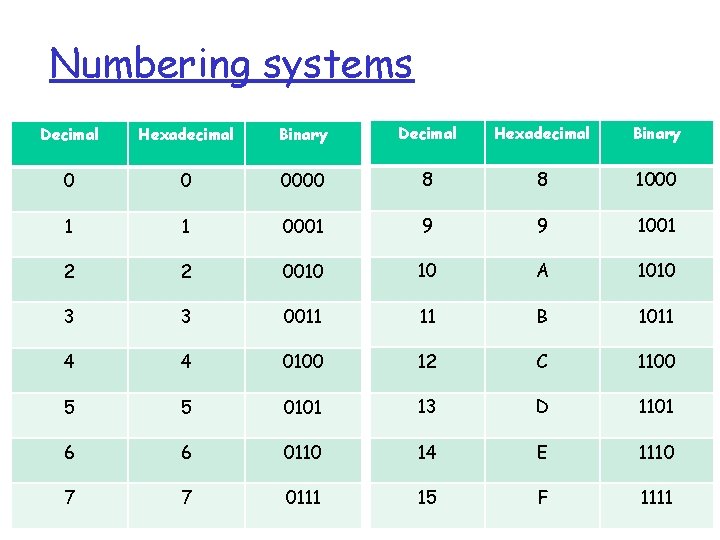
Numbering systems Decimal Hexadecimal Binary 0 0 0000 8 8 1000 1 1 0001 9 9 1001 2 2 0010 10 A 1010 3 3 0011 11 B 1011 4 4 0100 12 C 1100 5 5 0101 13 D 1101 6 6 0110 14 E 1110 7 7 0111 15 F 1111

Hexadecimal q Thus each byte is two hex digits (shorthand representation for human) q EX: Binary: 110010102 v How to represent this in hex representation? 110010102 q Separate them into nibbles 1100 1010 C A Hexadecimal representation: CA 16 q Try: convert 111101011002 to Hex representation

Converting Hex number to Binary q Converting hexadecimal numbers to binary is just the reverse operation of converting binary to hexadecimal. q Just convert each hexadecimal digit to its four-bit binary pattern. The resulting set of 1 s and 0 s is the binary equivalent of the hexadecimal number. q Convert A 5 B 916 to Binary.

Conversion: Hex and decimal q Hex to decimal v Exact similar to binary to decimal v Use base 16 v Try CA 16 q Decimal to Hex v Exactly similar to decimal to binary v Divide by 16 v Try 20210

Notes on Bases q Subscript is mandatory at least for a while. v v We use all three number bases. When a number is written, you should include the correct subscript. q Pronunciation v Binary and hexadecimal numbers are spoken by naming the digits followed by “binary” or “hexadecimal. ”

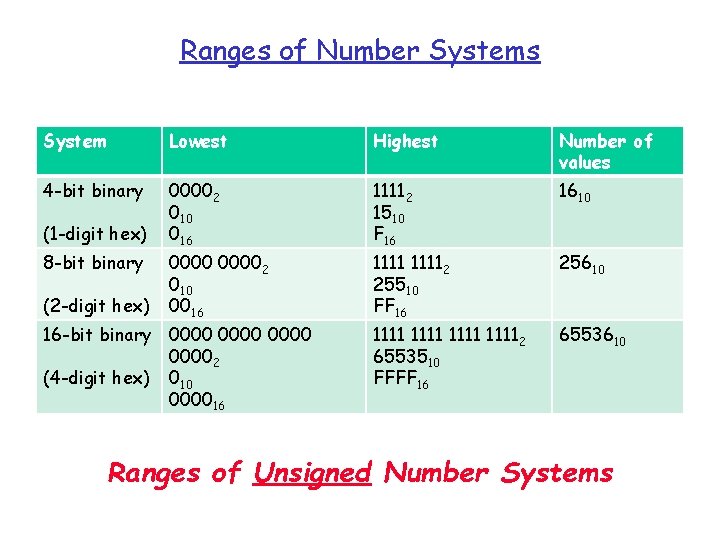
Ranges of Number Systems System Lowest Highest Number of values 4 -bit binary 00002 010 016 11112 1510 F 16 1610 00002 010 0016 11112 25510 FF 16 25610 11112 6553510 FFFF 16 6553610 (1 -digit hex) 8 -bit binary (2 -digit hex) 16 -bit binary 00002 (4 -digit hex) 010 000016 Ranges of Unsigned Number Systems

Electronic Prefixes q There is a set of terms used in electronics to represent very large values and very small values. q Kilo, Mega, Giga, Tera – used for representing very large values v E. g. , Kilo. Byte, Mega. Byte etc. q milli, micro, nano, pico – used for representing very small values v E. g. , milliseconds, microseconds etc.

Reading assignment q In Blackboard: v reading 02_08_29_2012. pdf v reading 03_08_29_2012. pdf

Practice problems q Let us do some quick example problems …