Lecture 2 Benchmarks Performance Metrics Cost Instruction Set

Lecture 2: Benchmarks, Performance Metrics, Cost, Instruction Set Architecture Professor Alvin R. Lebeck Computer Science 220 Fall 2001

Administrative • Some textbooks here, more to arrive Friday afternoon • Read Chapter 3 • Homework #1 Due September 11 – Simple scalar, read some of the documentation first – See web page for details – Questions, contact Fareed (fareed@cs. duke. edu) • Policy on Academic Integrity (Cheating. . ) • Homework – Discussion of topics is encouraged, peers are great resource – But, hand in your work • Projects – Work in pairs, learn how to collaborate. © Alvin R. Lebeck 2001 2

Review • Designing to Last through Trends Capacity Speed Logic 2 x in 3 years DRAM 4 x in 3 years 1. 4 x in 10 years Disk 4 x in 3 years 1. 4 x in 10 years • Time to run the task – Execution time, response time, latency • Tasks per day, hour, week, sec, ns, … – Throughput, bandwidth • “X is n times faster than Y” means Ex. Time(Y) ----Ex. Time(X) © Alvin R. Lebeck 2001 = Performance(X) -------Performance(Y) 3
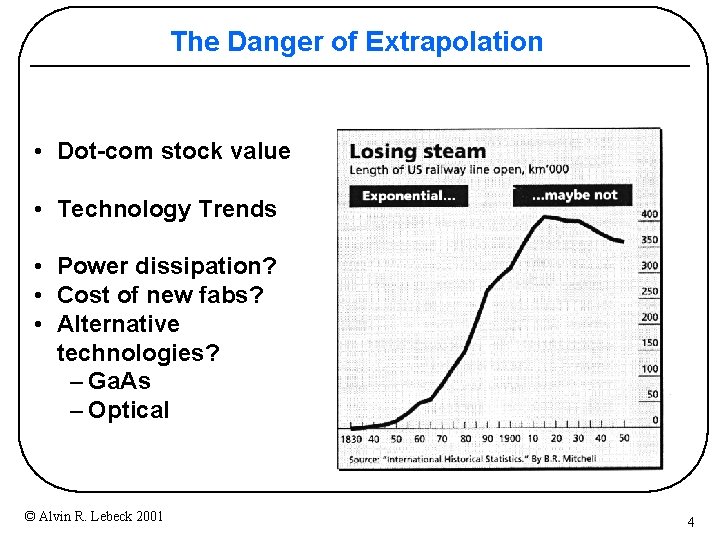
The Danger of Extrapolation • Dot-com stock value • Technology Trends • Power dissipation? • Cost of new fabs? • Alternative technologies? – Ga. As – Optical © Alvin R. Lebeck 2001 4
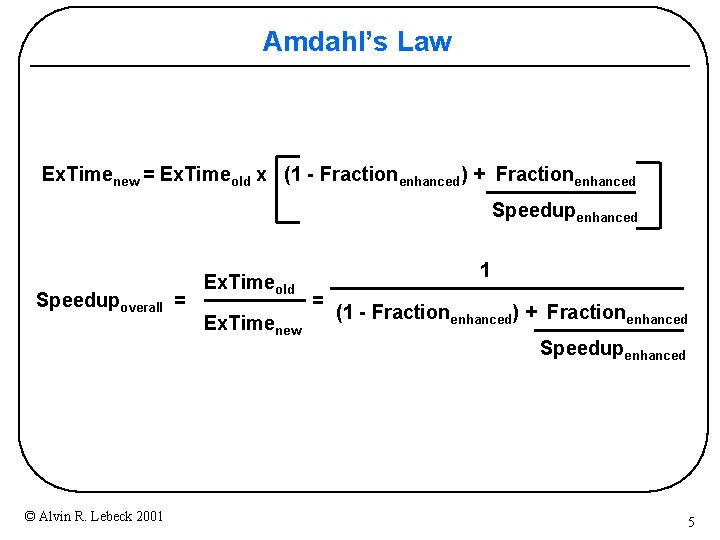
Amdahl’s Law Ex. Timenew = Ex. Timeold x (1 - Fractionenhanced) + Fractionenhanced Speedupoverall = © Alvin R. Lebeck 2001 Ex. Timeold Ex. Timenew 1 = (1 - Fractionenhanced) + Fractionenhanced Speedupenhanced 5
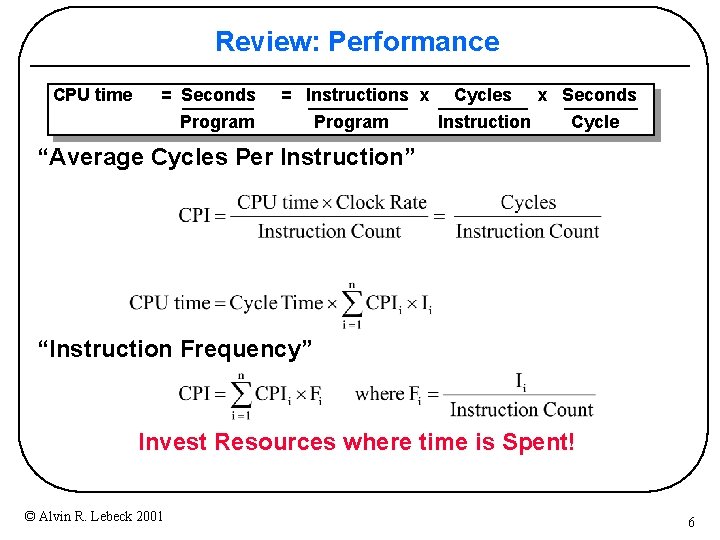
Review: Performance CPU time = Seconds = Instructions x Cycles Program Instruction Program x Seconds Cycle “Average Cycles Per Instruction” “Instruction Frequency” Invest Resources where time is Spent! © Alvin R. Lebeck 2001 6

Example Add register / memory operations: – One source operand in memory – One source operand in register – Cycle count of 2 Branch cycle count to increase to 3. What fraction of the loads must be eliminated for this to pay off? Base Machine (Reg / Reg) Op Freq Cycles ALU 50% 1 Load 20% 2 Typical Mix Store 10% 2 Branch 20% 2 © Alvin R. Lebeck 2001 7

Example Solution Exec Time = Instr Cnt x CPI x Clock Op Freq ALU. 50 Load. 20 Store. 10 Branch. 20 Reg/Mem 1. 00 Cycles CPI 1. 5 2. 4 2. 2 2. 3 1. 5 Freq Cycles CPI. 5 – X 1. 5 – X. 2 – X 2. 4 – 2 X. 1 2. 2. 2 3. 6 X 2 2 X 1–X (1. 7 – X)/(1 – X) Cycles. New Instructions. New CPINew must be normalized to new instruction frequency © Alvin R. Lebeck 2001 8

Example Solution Exec Time = Instr Cnt x CPI x Clock Op Freq ALU. 50 Load. 20 Store. 10 Branch. 20 Reg/Mem 1. 00 Cycles 1 2 2 2 . 5. 4. 2. 3 Freq. 5 – X. 2 – X. 1. 2 1. 5 1–X Cycles 1. 5 – X 2. 4 – 2 X 2. 2 3. 6 X 2 2 X (1. 7 – X)/(1 – X) Instr Cnt. Old x CPIOld x Clock. Old = Instr Cnt. New x CPINew x Clock. New 1. 00 x 1. 5 = (1 – X) x (1. 7 – X)/(1 – X) 1. 5 = 1. 7 – X 0. 2 = X ALL loads must be eliminated for this to be a win! © Alvin R. Lebeck 2001 9

Programs to Evaluate Processor Performance • (Toy) Benchmarks – 10 -100 line program – e. g. : sieve, puzzle, quicksort • Synthetic Benchmarks – Attempt to match average frequencies of real workloads – e. g. , Whetstone, dhrystone • Kernels – Time critical excerpts of real programs – e. g. , Livermore loops • Real programs – e. g. , gcc, compress, database, graphics, etc. © Alvin R. Lebeck 2001 10

Benchmarking Games • Differing configurations used to run the same workload on two systems • Compiler wired to optimize the workload • Test specification written to be biased towards one machine • Workload arbitrarily picked • Very small benchmarks used • Benchmarks manually translated to optimize performance © Alvin R. Lebeck 2001 11

Common Benchmarking Mistakes • • • Not validating measurements Collecting too much data but doing too little analysis Only average behavior represented in test workload Loading level (other users) controlled inappropriately Caching effects ignored Buffer sizes not appropriate Inaccuracies due to sampling ignored Ignoring monitoring overhead Not ensuring same initial conditions Not measuring transient (cold start) performance Using device utilizations for performance comparisons © Alvin R. Lebeck 2001 12

SPEC: System Performance Evaluation Cooperativeã • First Round 1989 – 10 programs yielding a single number • Second Round 1992 – Spec. Int 92 (6 integer programs) and Spec. FP 92 (14 floating point programs) » Compiler Flags unlimited. March 93 of DEC 4000 Model 610: – spice: unix. c: /def=(sysv, has_bcopy, ”bcopy(a, b, c)= memcpy(b, a, c)” – wave 5: /ali=(all, dcom=nat)/ag=a/ur=4/ur=200 – nasa 7: /norecu/ag=a/ur=4/ur 2=200/lc=blas • Third Round 1995 – Single flag setting for all programs; new set of programs “benchmarks useful for 3 years” • SPEC 2000: two options 1) specific flags 2) whatever you want © Alvin R. Lebeck 2001 13
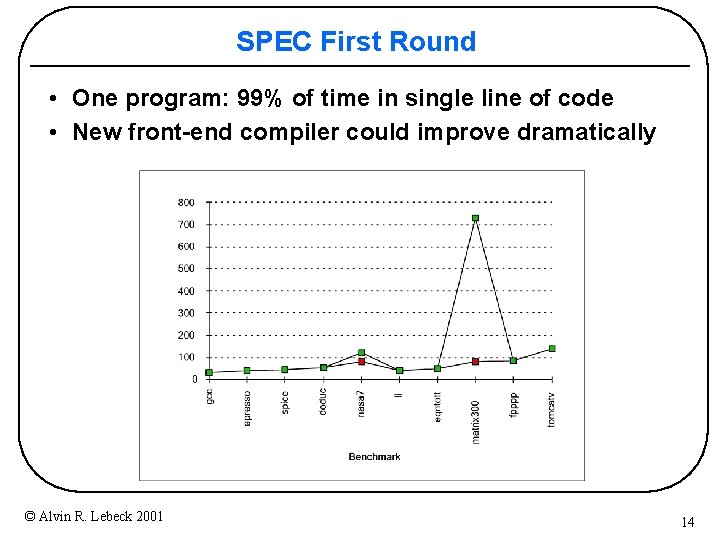
SPEC First Round • One program: 99% of time in single line of code • New front-end compiler could improve dramatically © Alvin R. Lebeck 2001 14

How to Summarize Performance • Arithmetic mean (weighted arithmetic mean) tracks execution time: å(Ti)/n or å(Wi*Ti) • Harmonic mean (weighted harmonic mean) of rates (e. g. , MFLOPS) tracks execution time: n/ å(1/Ri) or 1/ å(Wi/Ri) • Normalized execution time is handy for scaling performance • But do not take the arithmetic mean of normalized execution time, use the geometric mean (å Ri 1/n) © Alvin R. Lebeck 2001 15

Reporting Results • Reproducibility • List everything another researcher needs to duplicate the results • May include archiving your simulation/software infrastructure • Processor, cache hierarchy, main memory, disks, compiler version and optimization flags, OS version, application inputs, etc. © Alvin R. Lebeck 2001 16

Performance Evaluation • Given sales is a function of performance relative to the competition, big investment in improving product as reported by performance summary • Good products created when you have: – Good benchmarks – Good ways to summarize performance • If benchmarks/summary inadequate, then choose between improving product for real programs vs. improving product to get more sales; Sales almost always wins! • Ex. time or bandwidth is the measure of computer performance! • What about cost? © Alvin R. Lebeck 2001 17
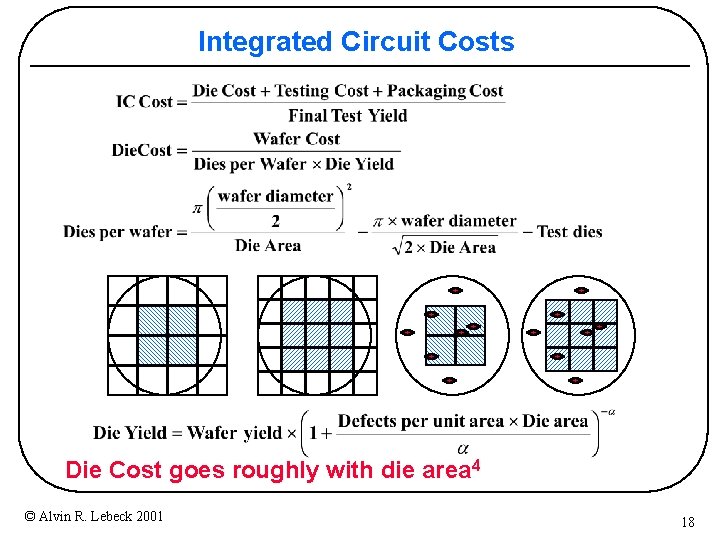
Integrated Circuit Costs Die Cost goes roughly with die area 4 © Alvin R. Lebeck 2001 18
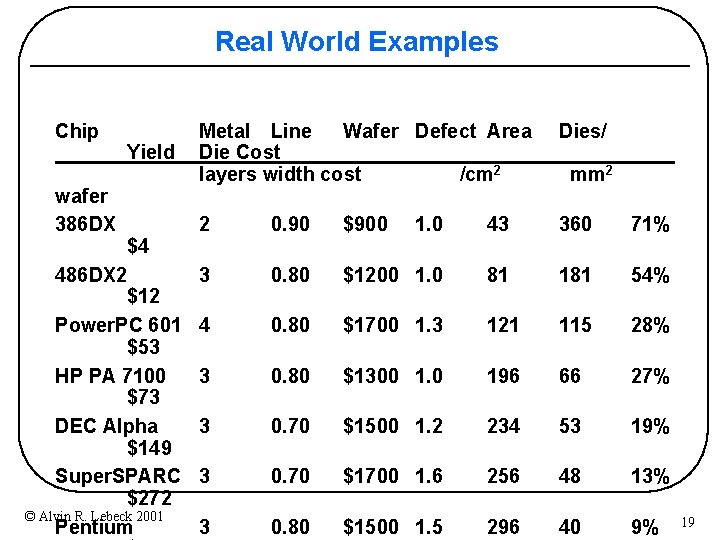
Real World Examples Chip wafer 386 DX Yield $4 486 DX 2 $12 Power. PC 601 $53 HP PA 7100 $73 DEC Alpha $149 Super. SPARC $272 © Alvin R. Lebeck 2001 Pentium Metal Line Wafer Defect Area Die Cost layers width cost /cm 2 Dies/ 2 0. 90 $900 1. 0 43 360 71% 3 0. 80 $1200 1. 0 81 181 54% 4 0. 80 $1700 1. 3 121 115 28% 3 0. 80 $1300 1. 0 196 66 27% 3 0. 70 $1500 1. 2 234 53 19% 3 0. 70 $1700 1. 6 256 48 13% 3 0. 80 $1500 1. 5 296 40 9% mm 2 19
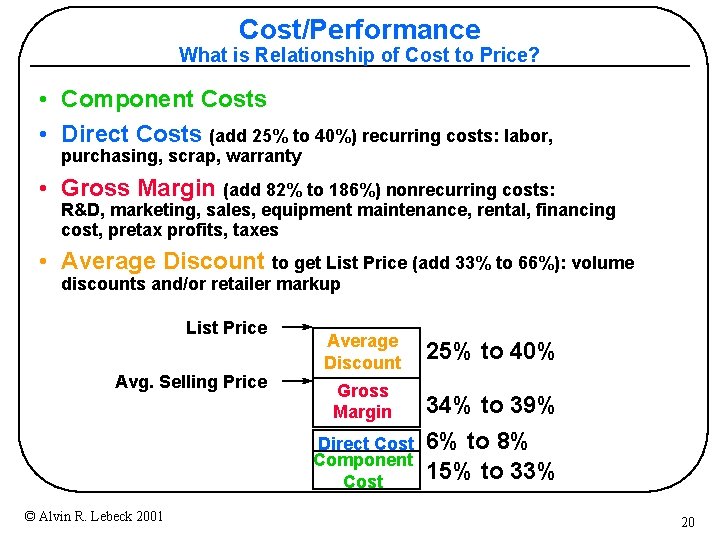
Cost/Performance What is Relationship of Cost to Price? • Component Costs • Direct Costs (add 25% to 40%) recurring costs: labor, purchasing, scrap, warranty • Gross Margin (add 82% to 186%) nonrecurring costs: R&D, marketing, sales, equipment maintenance, rental, financing cost, pretax profits, taxes • Average Discount to get List Price (add 33% to 66%): volume discounts and/or retailer markup List Price Avg. Selling Price Average Discount Gross Margin Direct Cost Component Cost © Alvin R. Lebeck 2001 25% to 40% 34% to 39% 6% to 8% 15% to 33% 20

Instruction Set Architecture

Instruction Set Architecture • 1950 s to 1960 s: Computer Architecture Course Computer Arithmetic • 1970 to mid 1980 s: Computer Architecture Course Instruction Set Design, especially ISA appropriate for compilers • 1990 s: Computer Architecture Course Design of CPU, memory system, I/O system, Multiprocessors • 2000 s: Computer Architecture Course – – Power issues Wire delays (distributed microarchitecture) New technologies New applications (media, network, etc. ) © Alvin R. Lebeck 2001 22
![Computer Architecture? . . . the attributes of a [computing] system as seen by Computer Architecture? . . . the attributes of a [computing] system as seen by](http://slidetodoc.com/presentation_image_h/bfb2f453eb9c104066ba59f407e7e351/image-23.jpg)
Computer Architecture? . . . the attributes of a [computing] system as seen by the programmer, i. e. the conceptual structure and functional behavior, as distinct from the organization of the data flows and controls the logic design, and the physical implementation. Amdahl, Blaaw, and Brooks, 1964 SOFTWARE © Alvin R. Lebeck 2001 23
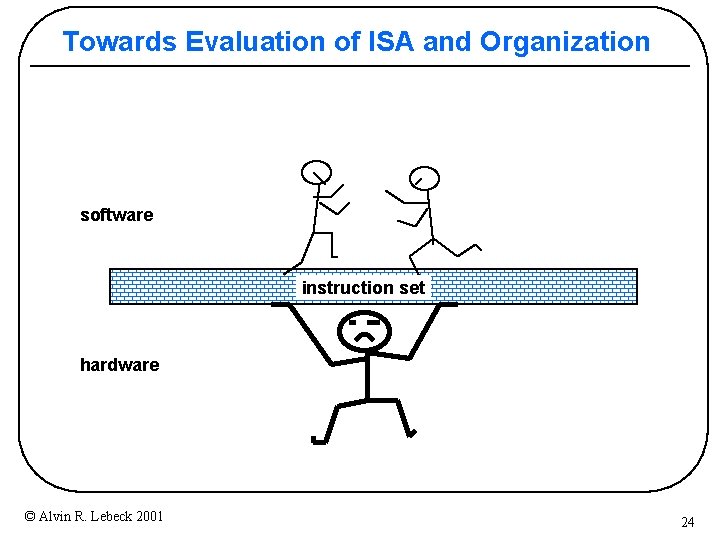
Towards Evaluation of ISA and Organization software instruction set hardware © Alvin R. Lebeck 2001 24
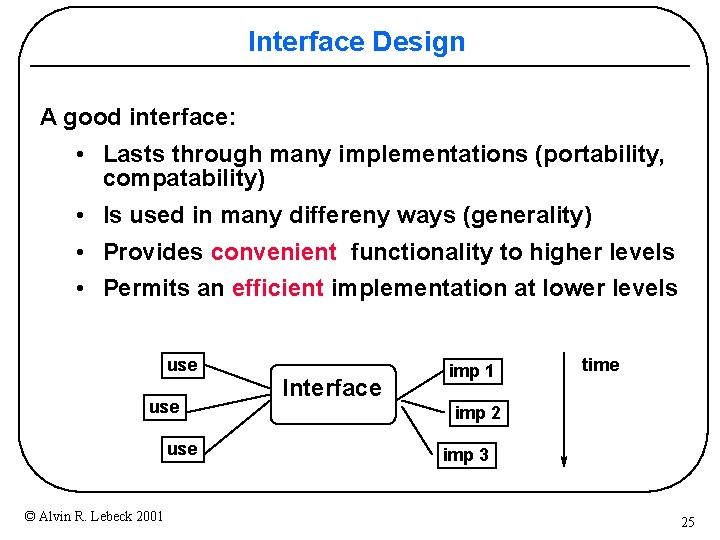
Interface Design A good interface: • Lasts through many implementations (portability, compatability) • Is used in many differeny ways (generality) • Provides convenient functionality to higher levels • Permits an efficient implementation at lower levels use use © Alvin R. Lebeck 2001 Interface imp 1 time imp 2 imp 3 25
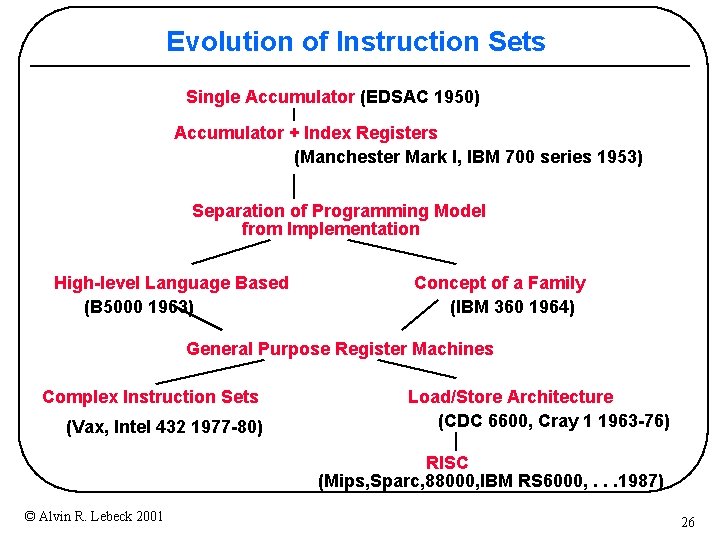
Evolution of Instruction Sets Single Accumulator (EDSAC 1950) Accumulator + Index Registers (Manchester Mark I, IBM 700 series 1953) Separation of Programming Model from Implementation High-level Language Based (B 5000 1963) Concept of a Family (IBM 360 1964) General Purpose Register Machines Complex Instruction Sets (Vax, Intel 432 1977 -80) Load/Store Architecture (CDC 6600, Cray 1 1963 -76) RISC (Mips, Sparc, 88000, IBM RS 6000, . . . 1987) © Alvin R. Lebeck 2001 26

Evolution of Instruction Sets • Major advances in computer architecture were typically associated with landmark instruction set designs – Ex: Stack vs GPR (System 360) • Design decisions must take into account: – – – technology machine organization programming langauges compiler technology operating systems • And they in turn influence these © Alvin R. Lebeck 2001 27
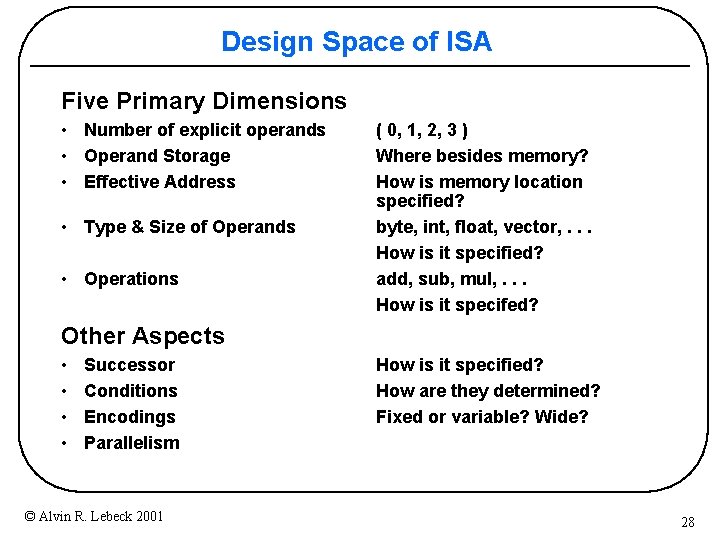
Design Space of ISA Five Primary Dimensions • Number of explicit operands • Operand Storage • Effective Address • Type & Size of Operands • Operations ( 0, 1, 2, 3 ) Where besides memory? How is memory location specified? byte, int, float, vector, . . . How is it specified? add, sub, mul, . . . How is it specifed? Other Aspects • • Successor Conditions Encodings Parallelism © Alvin R. Lebeck 2001 How is it specified? How are they determined? Fixed or variable? Wide? 28

ISA Metrics • Aesthetics: • Regularity (Orthogonality) – No special registers, few special cases, all operand modes available with any data type or instruction type • Primitives not solutions • Completeness – Support for a wide range of operations and target applications • Streamlined – Resource needs easily determined • • Ease of compilation (programming? ) Ease of implementation Scalability Density (Network BW and Power Consumption) © Alvin R. Lebeck 2001 29

Basic ISA Classes Accumulator: 1 address 1+x address add A addx A acc ¬ acc + mem[A] acc ¬ acc + mem[A + x] add tos ¬ tos + next (JAVA VM) Stack: 0 address General Purpose Register: 2 address 3 address add A B C A¬A+B A¬ B+C add Ra Rb Rc load Ra Rb store Ra Rb Ra ¬ Rb + Rc Ra ¬ mem[Rb] ¬ Ra Load/Store: 3 address © Alvin R. Lebeck 2001 30
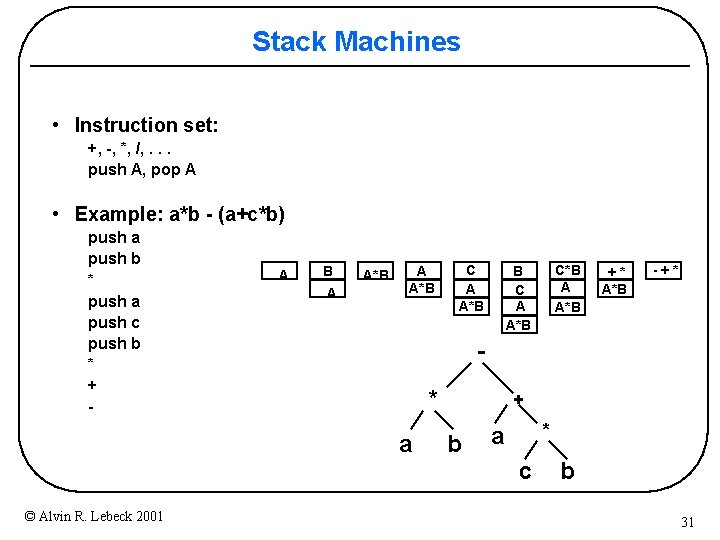
Stack Machines • Instruction set: +, -, *, /, . . . push A, pop A • Example: a*b - (a+c*b) push a push b * push a push c push b * + - A B A A*B C A A*B +* A*B -+* * a + b * a c © Alvin R. Lebeck 2001 C*B A A*B B C A A*B b 31

The Case Against Stacks • Performance is derived from the existence of several fast registers, not from the way they are organized • Data does not always “surface” when needed – Constants, repeated operands, common subexpressions • so TOP and Swap instructions are required • Code density is about equal to that of GPR instruction sets – Registers have short addresses – Keep things in registers and reuse them • Slightly simpler to write a poor compiler, but not an optimizing compiler • So, why JAVA? © Alvin R. Lebeck 2001 32
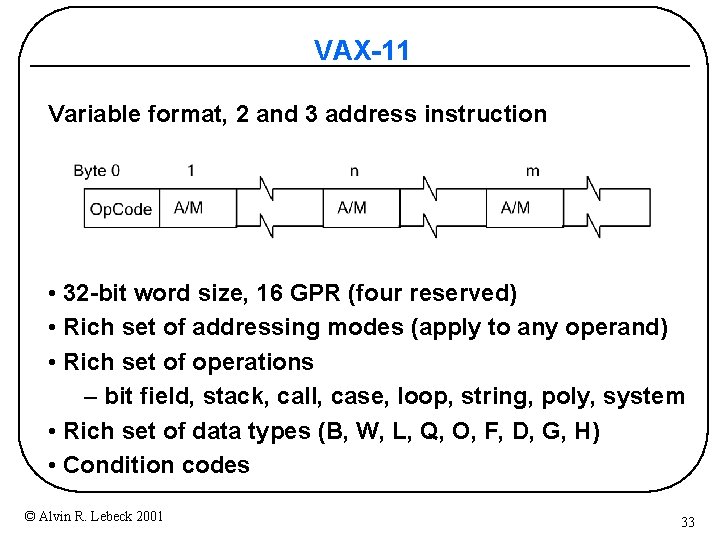
VAX-11 Variable format, 2 and 3 address instruction • 32 -bit word size, 16 GPR (four reserved) • Rich set of addressing modes (apply to any operand) • Rich set of operations – bit field, stack, call, case, loop, string, poly, system • Rich set of data types (B, W, L, Q, O, F, D, G, H) • Condition codes © Alvin R. Lebeck 2001 33
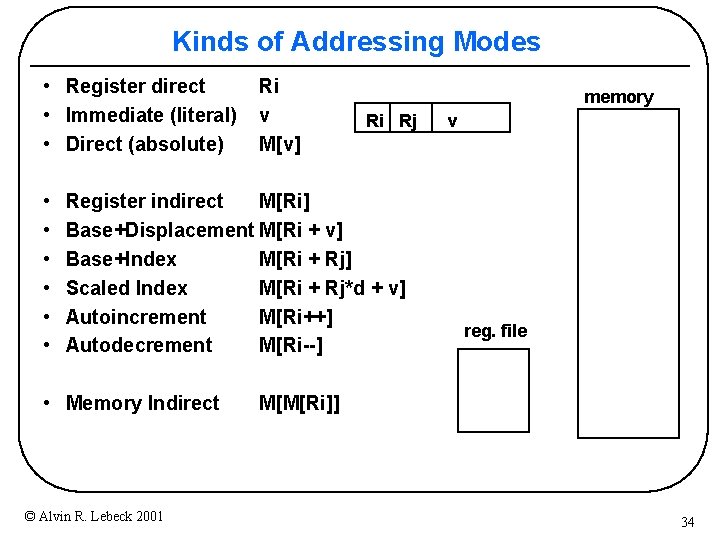
Kinds of Addressing Modes • Register direct • Immediate (literal) • Direct (absolute) • • • Ri v M[v] memory Ri Rj Register indirect M[Ri] Base+Displacement M[Ri + v] Base+Index M[Ri + Rj] Scaled Index M[Ri + Rj*d + v] Autoincrement M[Ri++] Autodecrement M[Ri--] • Memory Indirect © Alvin R. Lebeck 2001 v reg. file M[M[Ri]] 34

A "Typical" RISC • • 32 -bit fixed format instruction (3 formats) 32 64 -bit GPR (R 0 contains zero) 3 -address, reg-reg arithmetic instruction Single address mode for load/store: base + displacement – no indirection • Simple branch conditions • Delayed branch see: SPARC, MIPS, MC 88100, AMD 2900, i 960, i 860 PARisc, POWERPC, DEC Alpha, Clipper, CDC 6600, CDC 7600, Cray-1, Cray-2, Cray-3 © Alvin R. Lebeck 2001 35

Example: MIPS (like DLX) Register-Register 31 26 25 Op 21 20 Rs 1 16 15 Rs 2 11 10 6 5 Rd 0 Opx Register-Immediate 31 26 25 Op 21 20 Rs 1 16 15 0 immediate Rd Branch 31 26 25 Op Rs 1 21 20 16 15 Rs 2/Opx 0 immediate Jump / Call 31 26 25 Op © Alvin R. Lebeck 2001 0 target 36

Next Time • Data path design • Pipelining • Homework #1 Due Sept 11 © Alvin R. Lebeck 2001 37
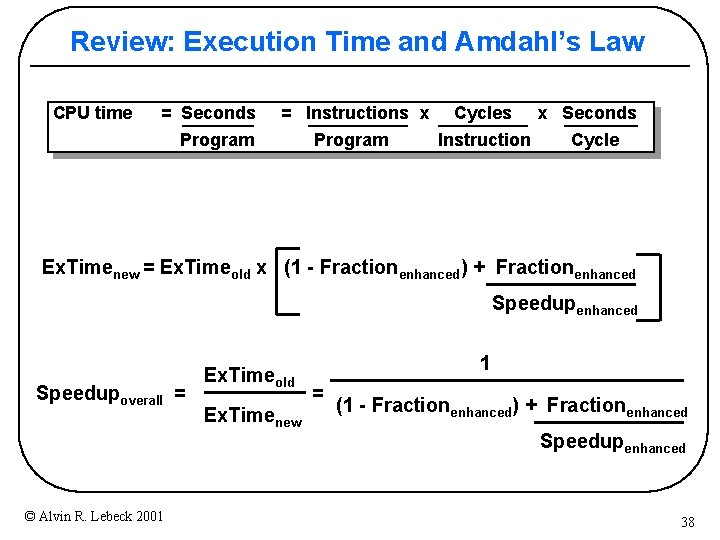
Review: Execution Time and Amdahl’s Law CPU time = Seconds = Instructions x Cycles Program Instruction Program x Seconds Cycle Ex. Timenew = Ex. Timeold x (1 - Fractionenhanced) + Fractionenhanced Speedupoverall = © Alvin R. Lebeck 2001 Ex. Timeold Ex. Timenew 1 = (1 - Fractionenhanced) + Fractionenhanced Speedupenhanced 38

Review: How to Summarize Performance • Arithmetic mean (weighted arithmetic mean) tracks execution time: å(Ti)/n or å(Wi*Ti) • Harmonic mean (weighted harmonic mean) of rates (e. g. , MFLOPS) tracks execution time: n/ å(1/Ri) or 1/ å(Wi/Ri) • Normalized execution time is handy for scaling performance • But do not take the arithmetic mean of normalized execution time, use the geometric mean (å (Ri)^1/n) © Alvin R. Lebeck 2001 39

Review: Performance Evaluation • • Benchmarks (toy, synthetic, kernels, full applications) Games Mistakes Influence of making the sale © Alvin R. Lebeck 2001 40
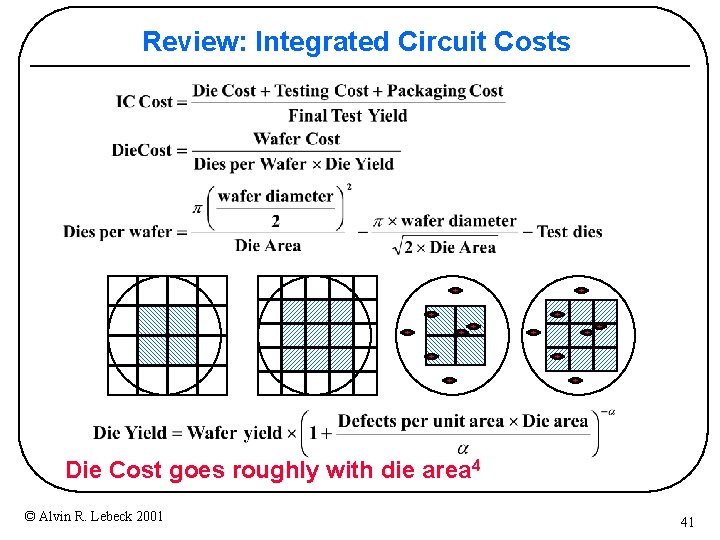
Review: Integrated Circuit Costs Die Cost goes roughly with die area 4 © Alvin R. Lebeck 2001 41
- Slides: 41