Lecture 2 Arrays Linear Data structures Linear form

Lecture 2 Arrays

Linear Data structures • Linear form a sequence • Linear relationship b/w the elements • represented by means of sequential memory location • Link list and arrays are linear relationship • Non-Linear Structure are Trees and Graphs

Operation performed by Linear Structure • Traversal: Processing each element in the list • Search : Find the location of the element with a given value or the record with a given key • Insertion : Adding new element to the list • Deletion : Removing an element from the list • Sorting : Arranging the elements in some type of order • Merging : Combining two list into single list

Linear Array • List of finite number N of homogenous data elements (i. e. data elements of same type) such that – The elements of the array are referenced respectively by an index set consisting of N consecutive number – The elements of the array are stored respectively in successive memory location

Length of Array • N = length of array Length = UB – LB + 1 – UB = Upper Bound or Largest Index – LB= Lower Bound or smallest Index

Representation in Memory • Address of any element in Array = LOC(LA[k])=Base (LA) + w (k - LB) – LOC(LA[k]) =Address of element LA[k] of the Array LA – Base (LA) = Base Address of LA – w = No. of words per memory cell for the Array LA – k = Any element of Array

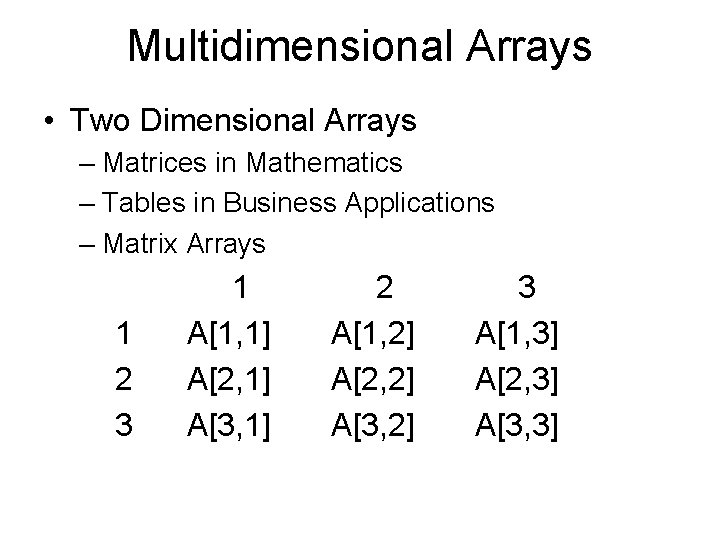
Multidimensional Arrays • Two Dimensional Arrays – Matrices in Mathematics – Tables in Business Applications – Matrix Arrays 1 2 3 1 A[1, 1] A[2, 1] A[3, 1] 2 A[1, 2] A[2, 2] A[3, 2] 3 A[1, 3] A[2, 3] A[3, 3]

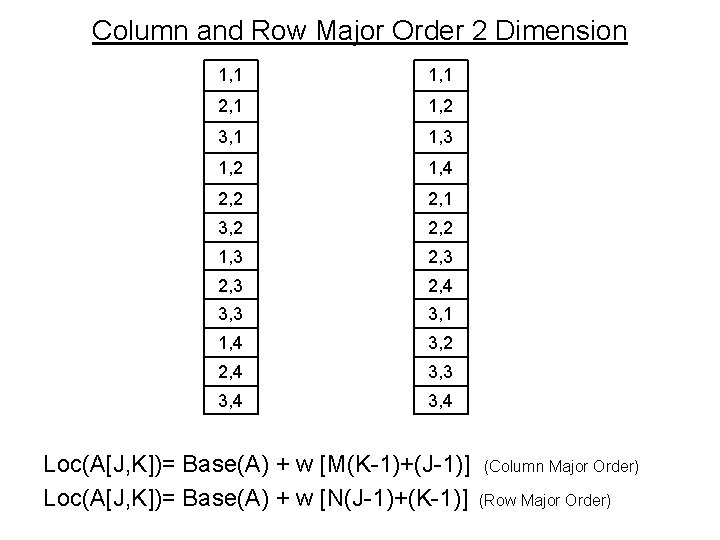
Column and Row Major Order 2 Dimension 1, 1 2, 1 1, 2 3, 1 1, 3 1, 2 1, 4 2, 2 2, 1 3, 2 2, 2 1, 3 2, 4 3, 3 3, 1 1, 4 3, 2 2, 4 3, 3 3, 4 Loc(A[J, K])= Base(A) + w [M(K-1)+(J-1)] Loc(A[J, K])= Base(A) + w [N(J-1)+(K-1)] (Column Major Order) (Row Major Order)

Column and Row Major Order 3 Dimension 1, 1, 1 2, 1, 1, 2, 1 1, 1, 3 2, 2, 1 1, 3, 1 1, 2, 2 2, 3, 1 1, 2, 3 1, 4, 1 1, 3, 1 2, 4, 1 1, 3, 2 … … 1, 4, 3 2, 4, 2 2, 4, 3 Length = Upper Bound – Lower Bound +1 Effective Index = Index Number – Lower Bound

Column and Row Major Order 3 Dimension Length = Upper Bound – Lower Bound +1 Effective Index = Index Number – Lower Bound Row Major Order: Loc = Base + w(E 1 L 2+E 2)L 3+E 3) Column Major Order: Loc = Base + w(E 3 L 2+E 2)L 1+E 1)

Column and Row Major Order 3 Dimension Row Major Order: Column Major Order: B ( 2 : 8 , - 4 : 1 , 6 : 10 ) B ( 1 : 8 , - 5 : 5 , - 10 : 5 ) L 1 = 8 – 2 + 1 = 7 L 2 = 1 - ( - 4 ) + 1 = 6 L 3 = 10 - 6 + 1 = 5 L 1 = 8 – 1 + 1 = 8 L 2 = 5 - ( - 5 ) + 1 = 11 L 3 = 5 - ( - 10 ) + 1 = 16 E 1 = 5 – 2 = 3 E 2 = - 1 - ( - 4 ) = 3 E 3 = 8 - 6 = 2 E 1 = 3 – 1 = 2 E 2 = 3 - ( - 5 ) = 8 E 3 = 3 - ( - 10 ) = 13 E 1. L 2 = 3. 6 = 18 E 1. L 2 + E 2 = 18 + 3 = 21 ( E 1. L 2 + E 2 ). L 3 = 21. 5 = 105 (E 1. L 2 + E 2). L 3 + E 3 = 105+2 =107 E 3. L 2 = 13. 11 = 143 E 3. L 2 + E 2 = 143 + 8 = 151 ( E 3. L 2 + E 2 ). L 1 = 151. 8 = 1208 (E 3. L 2 + E 2). L 1 + E 1 = 1208+2 =1210 Loc = Base + w(E 1 L 2+E 2)L 3+E 3) Loc = Base + w(E 3 L 2+E 2)L 1+E 1) Loc [5, -1, 8] = 200 + 4 (107) = 628 Loc [3, 3, 3] = 400 + 4 (1210) = 5240

Operations on Array • Traversing a Linear Array Traverse. Array (LA, LB, UB) Function: This algorithm traverse LA applying an operation PROCESS to each element of LA Input: LA is a Linear Array with Lower Bound LB and Upper bound UB

Algorithm: 1. [Initialize Counter] Set K: =LB 2. Repeat Steps 3 and 4 while K≤UB 3. [Visit element] Apply PROCESS to LA[K] 4. [Increase counter] Set K: =K+1 [End of Step 2 loop] 5. Exit

Operations Cont…. • Insert an element in Linear Array Insert. Element (LA, ITEM, N, K) Function: This algorithm insert an element in a Linear Array at required position Input: LA is a Linear Array having N elements ITEM is the element to be inserted at given position K Precondition: K≤N where K is a +ve integer

Algorithm: 1. [Initialize Counter] Set J: =N 2. Repeat Steps 3 and 4 while J≥K 3. [Move Jth element downward] Set LA[J+1] : = LA[J] 4. [Decrease counter] Set J: =J-1 [End of Step 2 loop] 5. [Insert element] Set LA[K]: =ITEM 6. [Reset N] N: = N+1 7. Exit

Operation Cont…. • Delete an element from a Linear Array Delete. Element (LA, ITEM, N, K) Function: This algorithm delete an element from a given position in Linear Array Input: LA is a Linear Array having N elements K is the position given from which ITEM needs to be deleted Output: ITEM is the element deleted from the given position K Precondition: K≤N where K is a +ve integer

Algorithm: 1. Set ITEM: =LA[K] 2. Set J: = K 3. Repeat Steps 4 and 5 while J<N 4. [Move Jth element upward] Set LA[J] : = LA[J+1] 5. [Increase counter] Set J: =J+1 [End of Step 3 loop] 6. [Reset N] N: = N-1 7. Exit