Lecture 2 Analog to digital conversion Basic discrete
Lecture 2 Analog to digital conversion & Basic discrete signals
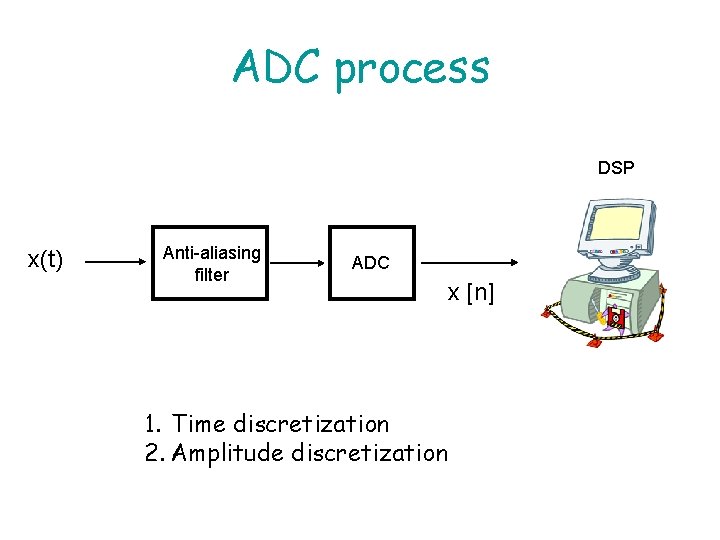
ADC process DSP x(t) Anti-aliasing filter ADC 1. Time discretization 2. Amplitude discretization x [n]
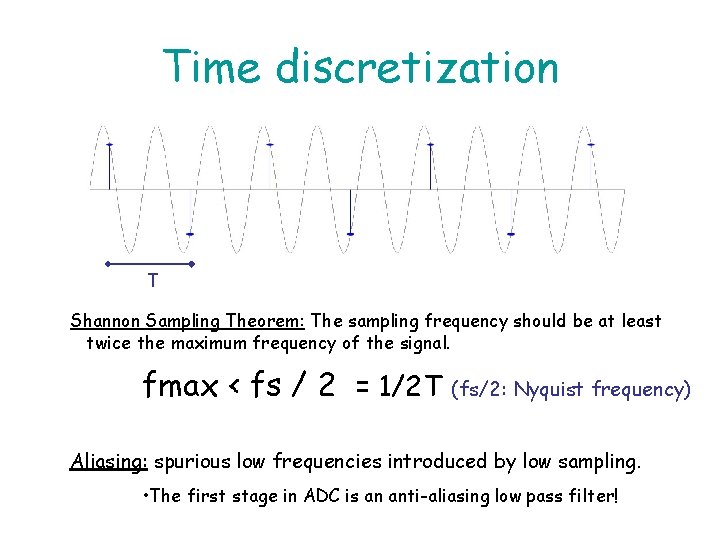
Time discretization T Shannon Sampling Theorem: The sampling frequency should be at least twice the maximum frequency of the signal. fmax < fs / 2 = 1/2 T (fs/2: Nyquist frequency) Aliasing: spurious low frequencies introduced by low sampling. • The first stage in ADC is an anti-aliasing low pass filter!
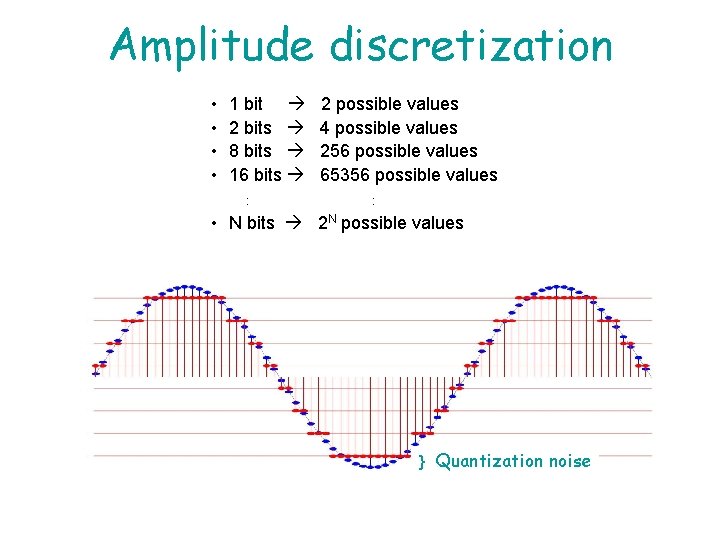
Amplitude discretization • • 1 bit 2 bits 8 bits 16 bits : 2 possible values 4 possible values 256 possible values 65356 possible values : • N bits 2 N possible values } Quantization noise
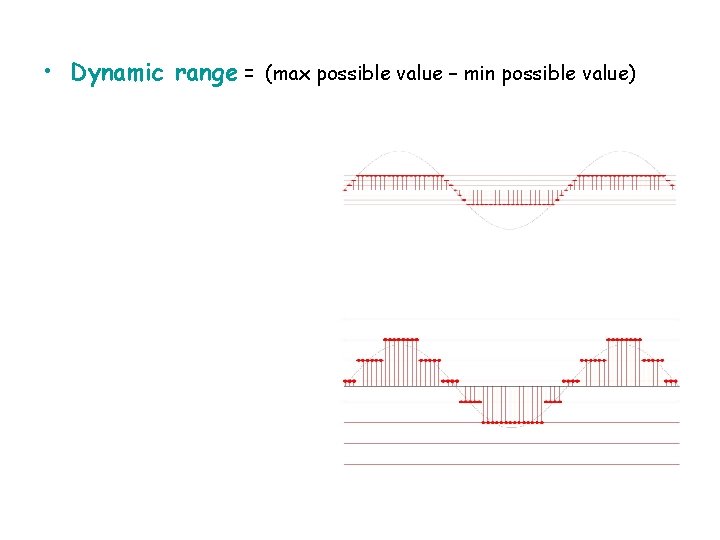
• Dynamic range = (max possible value – min possible value) – If too low • Good resolution • Risk of saturation – If too high • Poor resolution • No saturation
![DAC process DSP x [n] DAC Sample and hold Analog filter x(t)](http://slidetodoc.com/presentation_image/db5fb065137d2cbf60e69b635fbe3129/image-6.jpg "DAC process DSP x [n] DAC Sample and hold Analog filter x(t)")
DAC process DSP x [n] DAC Sample and hold Analog filter x(t)
Signal types • Continuous time • Continuous amplitude • Discrete time • Continuous amplitude • Continuous time • Discrete amplitude ü Digital signals
Basic digital signals Why ? ü Complex signals can usually be expressed as summation of simple ones. ü For linear DSPs, if we know the response to basic signals we can predict the response to more complex ones. ü They can be used as test signals for studying properties of DSPs.
![• Unit impulse function d [n] 1 n=0 d[n] = 1 n≠ 0](http://slidetodoc.com/presentation_image/db5fb065137d2cbf60e69b635fbe3129/image-9.jpg "• Unit impulse function d [n] 1 n=0 d[n] = 1 n≠ 0")
• Unit impulse function d [n] 1 n=0 d[n] = 1 n≠ 0 n=0 u[n] = 1 n<0 n≥ 0 n • Unit step function d [n] 1 n=0 n
![• Exponential function x [n] x[n] = A an n=0 0<a<1 n •](http://slidetodoc.com/presentation_image/db5fb065137d2cbf60e69b635fbe3129/image-10.jpg "• Exponential function x [n] x[n] = A an n=0 0<a<1 n •")
• Exponential function x [n] x[n] = A an n=0 0<a<1 n • Sinusoidal function x [n] 1 x[n] = A cos(w n + f) n=0 n
![Periodicity • A signal is periodic if repeats after T values: x [n] =](http://slidetodoc.com/presentation_image/db5fb065137d2cbf60e69b635fbe3129/image-11.jpg "Periodicity • A signal is periodic if repeats after T values: x [n] =")
Periodicity • A signal is periodic if repeats after T values: x [n] = x [n+T] = x [n+2 T] = … T is the period of the signal • Exercise: Calculate the period of: a) x [n] = cos (Πn/4) b) x [n] = cos (3Πn/4)
![Exercise: Draw the following sequences: 1. 2. 3. 4. 5. 6. x [n] =](http://slidetodoc.com/presentation_image/db5fb065137d2cbf60e69b635fbe3129/image-12.jpg "Exercise: Draw the following sequences: 1. 2. 3. 4. 5. 6. x [n] =")
Exercise: Draw the following sequences: 1. 2. 3. 4. 5. 6. x [n] = u[n-2] x [n] = n u[n] x [n] = -3 d[n+4] x [n] = an a > 1 x [n] = -2 u[-n-2] x [n] = u[n+2] – u[n-6]
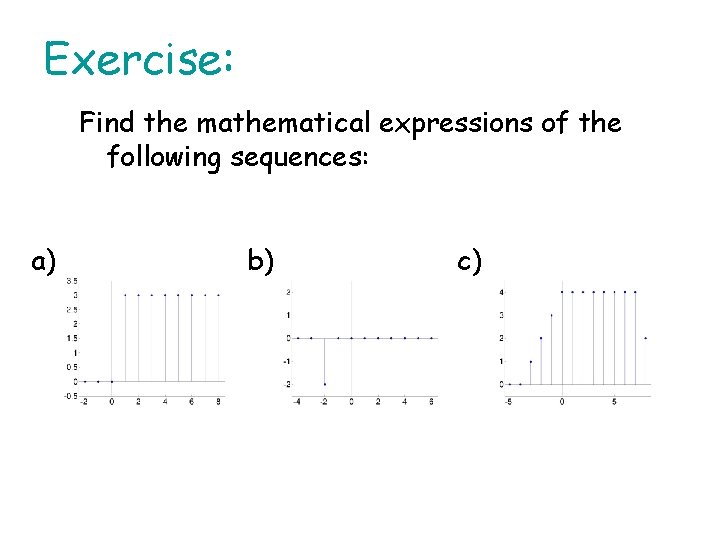
Exercise: Find the mathematical expressions of the following sequences: a) b) c)
![Exercise: Given the sequence of the figure, draw the following sequences: • a) x[n-2]](http://slidetodoc.com/presentation_image/db5fb065137d2cbf60e69b635fbe3129/image-14.jpg "Exercise: Given the sequence of the figure, draw the following sequences: • a) x[n-2]")
Exercise: Given the sequence of the figure, draw the following sequences: • a) x[n-2] • b) x[3 -n] • c) x[n-1] u[n] • d) x[n-1] d[n] • e) x[1 -n] d[n-2]
- Slides: 14