Lecture 2 Abstract Data Types Implementations of SetsDictionaries

Lecture 2. Abstract Data Types, Implementations of Sets/Dictionaries Cp. Sc 212: Algorithms and Data Structures Brian C. Dean School of Computing Clemson University Fall, 2012
![Fundamental Data Structures A[0] A[N– 1] Arrays NULL head Linked Lists Linked list questions Fundamental Data Structures A[0] A[N– 1] Arrays NULL head Linked Lists Linked list questions](http://slidetodoc.com/presentation_image_h2/84179d1fb37ef0834547c87123577bdb/image-2.jpg)
Fundamental Data Structures A[0] A[N– 1] Arrays NULL head Linked Lists Linked list questions are particularly popular in job interviews; e. g. , - Insert or delete a node in a linked list - Reverse a linked list 2
![Array and Linked List Performance A[0] A[N– 1] • Retrieve or modify any element Array and Linked List Performance A[0] A[N– 1] • Retrieve or modify any element](http://slidetodoc.com/presentation_image_h2/84179d1fb37ef0834547c87123577bdb/image-3.jpg)
Array and Linked List Performance A[0] A[N– 1] • Retrieve or modify any element in O(1) time. • Insert or delete in middle of list: O(N) time. • Insert or delete from ends: O(1) time – Be careful not to run over end of allocated memory – Possibly consider using a “circular” array… head • Seek to any position in list: O(N) time. • Then insert or delete element: O(1) time. • Insert or delete from ends: O(1) time. NULL 3
![Circular Arrays, Queues A[0] back front A[N– 1] back • First-In, First-Out (FIFO). • Circular Arrays, Queues A[0] back front A[N– 1] back • First-In, First-Out (FIFO). •](http://slidetodoc.com/presentation_image_h2/84179d1fb37ef0834547c87123577bdb/image-4.jpg)
Circular Arrays, Queues A[0] back front A[N– 1] back • First-In, First-Out (FIFO). • Could be implemented using linked lists instead… void insert(int x) { A[front] = x; front = (front+1) % N; } int remove(void) { int result = A[back]; back = (back+1) % N; return result; } 4
![Circular Arrays, Queues A[0] back front A[N– 1] back • First-In, First-Out (FIFO). • Circular Arrays, Queues A[0] back front A[N– 1] back • First-In, First-Out (FIFO). •](http://slidetodoc.com/presentation_image_h2/84179d1fb37ef0834547c87123577bdb/image-5.jpg)
Circular Arrays, Queues A[0] back front A[N– 1] back • First-In, First-Out (FIFO). • Could be implemented using linked lists instead… • Example: “cat file | grep algorithm | wc –l” counts the number of lines in file containing “algorithm”. Queues are used to send data from one program to the next along the pipeline. 5
![Stacks top A[0] • Last-In, First-Out (LIFO). • Could also be implemented with a Stacks top A[0] • Last-In, First-Out (LIFO). • Could also be implemented with a](http://slidetodoc.com/presentation_image_h2/84179d1fb37ef0834547c87123577bdb/image-6.jpg)
Stacks top A[0] • Last-In, First-Out (LIFO). • Could also be implemented with a linked list. . . void push(int x) { A[top++] = x; } int pop(void) { return A[--top]; }
![Stacks top A[0] • Example: A stack is used to store the state of Stacks top A[0] • Example: A stack is used to store the state of](http://slidetodoc.com/presentation_image_h2/84179d1fb37ef0834547c87123577bdb/image-7.jpg)
Stacks top A[0] • Example: A stack is used to store the state of unfinished function calls. For example… void what_does_this_do(int n) { if (n==0) return; printf (“%dn”, n); what_does_this_do(n-1); printf (“%dn”, n); }

An Important Distinction… Specification of a data structure in terms of the operations it needs to support. A concrete approach for implementation of the data structure that fulfills these requirements. (sometimes called an abstract data type) 8
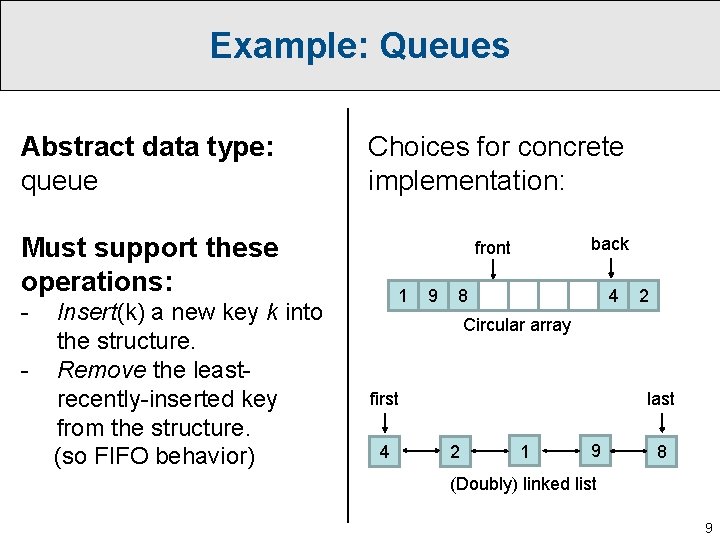
Example: Queues Abstract data type: queue Choices for concrete implementation: Must support these operations: front - Insert(k) a new key k into the structure. Remove the leastrecently-inserted key from the structure. (so FIFO behavior) 1 9 back 8 4 2 Circular array last first 4 2 1 9 8 (Doubly) linked list 9
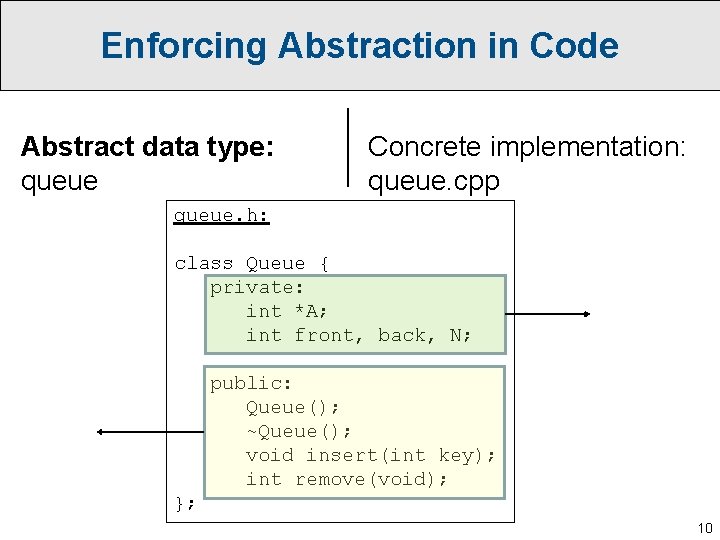
Enforcing Abstraction in Code Abstract data type: queue Concrete implementation: queue. cpp queue. h: class Queue { private: int *A; int front, back, N; public: Queue(); ~Queue(); void insert(int key); int remove(void); }; 10
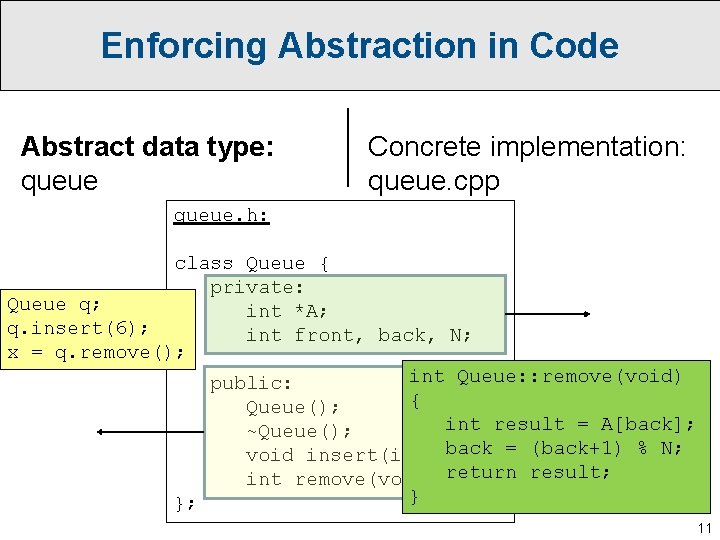
Enforcing Abstraction in Code Abstract data type: queue Concrete implementation: queue. cpp queue. h: class Queue { private: Queue q; int *A; q. insert(6); int front, back, N; x = q. remove(); int Queue: : remove(void) public: { Queue(); int result = A[back]; ~Queue(); back = (back+1) % N; void insert(int key); int remove(void); return result; } }; 11

Example: Sets / Dictionaries Abstract data type: set / dictionary Choices for concrete implementation: Must support these operations: 1 - 5 - Insert(k) a new key k into the structure. Remove(k) a key k in the structure. Find(k) whether a key is in the structure. Enumerate all keys in structure (in any order). 2 3 5 8 Sorted array 8 1 3 2 Unsorted array 1 2 3 5 8 Sorted (doubly) linked list 5 8 1 3 2 Unsorted (doubly) linked list 12
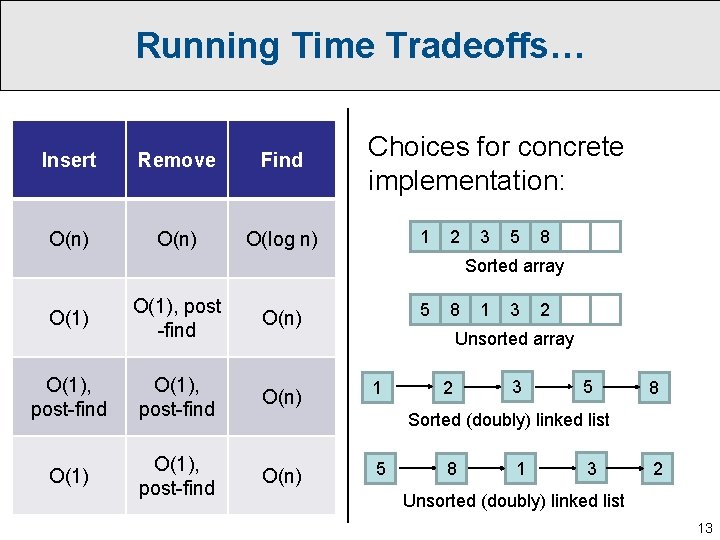
Running Time Tradeoffs… Insert Remove Find O(n) O(log n) Choices for concrete implementation: 1 2 3 5 8 Sorted array O(1), post -find O(n) O(1), post-find O(n) 5 8 1 3 2 Unsorted array 1 2 3 5 8 Sorted (doubly) linked list 5 8 1 3 2 Unsorted (doubly) linked list 13
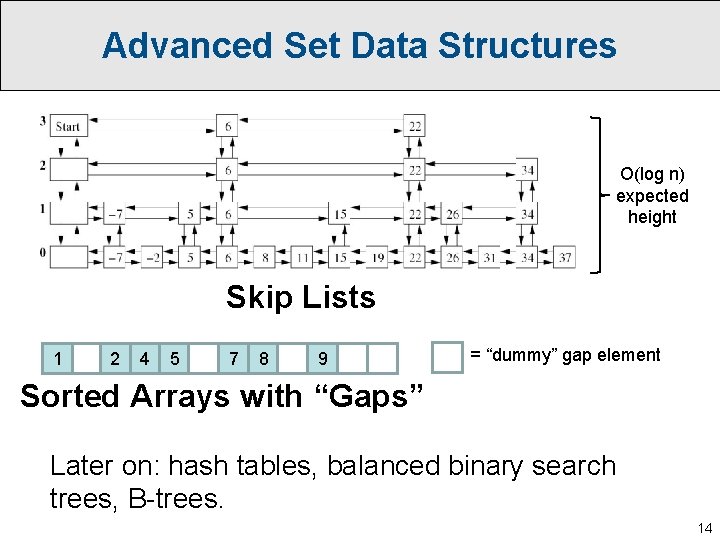
Advanced Set Data Structures O(log n) expected height Skip Lists 1 2 4 5 7 8 9 = “dummy” gap element Sorted Arrays with “Gaps” Later on: hash tables, balanced binary search trees, B-trees. 14

Skip Lists: Summary • Each level contains roughly half the elements of the level below it. • Total space: roughly N + N/2 + N/4 + … = 2 N = O(N). • Expected height: O(log N) • O(log N) expected time for insert, remove, and find. • Insert uses randomization in a clever way: – Insert into level 0 first, and then flip a fair coin repeatedly. – Keep inserting into higher levels as long as we flip heads. • Find analyzed most easily in reverse: – Roughly half our steps go up, the others go left. – But we can step up only as many times as the max height of the skip list, which is O(log n) in expectation. 15

Arrays with Gaps • Store N array elements within a block of size, say, 1. 5 N, with regularly-spaced “gap” elements. • As long as gaps are regularly-spaced, we can still perform find with binary search in O(log N) time! • Remove just creates a new gap element. • Insert speeds up, since fewer elements need to be moved (just move them over until we reach a gap). • Tricky part: occasionally need to re-distribute the gaps to keep them regularly spaced. – Requires amortized analysis to analyze performance. – Implemented properly, insert and remove take O(log 2 N) amortized time. (slightly complicated though…) 16
- Slides: 16