Lecture 2 A Synchronous Machine Modeling Derivation of

Lecture 2 A Synchronous Machine Modeling Derivation of the dq 0 Equations of an Idealized Three-Phase Synchronous Machine Professor: Ali Keyhani

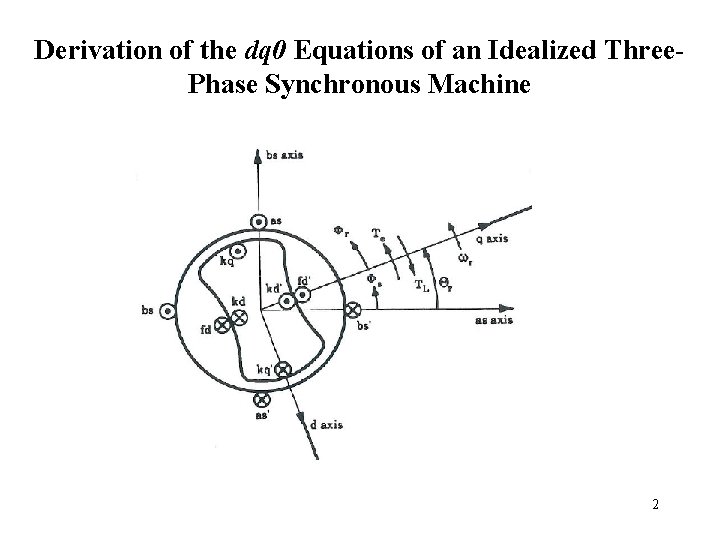
Derivation of the dq 0 Equations of an Idealized Three. Phase Synchronous Machine 2

Derivation of the dq 0 Equations of an Idealized Three. Phase Synchronous Machine Assumptions: 1) A stator inner periphery has uniform radius (Not a function of position around the gap) 2) A rotor outer periphery has non-uniform radius. The rotor, specifically, is shaped such that when the motor is excited by a single, full pitched, concentrated winding located on the stator, then the flux per unit length which exists from the stator into the air gap is a sinusoidal function of position around the gap. 3) Two sets of shorted rotor coils or bars (amortisseur windings) are located on the two axes of rotor, which, although not sinusoidally distributed, have induced in them sinusoidal mmf (current) distribution due to the coupling with the stator circuits. 3

Derivation of the dq 0 Equations of an Idealized Three -phase Synchronous Machine 4) 5) 6) 7) A third winding is located on one axis of rotor (d-axis, see Figure 1). Although this winding is generally concentrated, it is assumed that the winding produces same fundamental component of mmf around the gap. This is permissible since it was shown for two-phase case that the harmonic components of mmf give rise merely to a differential leakage flux component. Linear magnetic current (no saturation). This assumption will be relaxed later. Since the circuit is linear, it is assumed that the stator and rotor iron (finite) can be replaced by material having infinite permeability. It is assumed that the gap can be increased to account for this effect. Constant electrical parameters (i. e. R, L, C) independent of temperature or frequency. The stator is connected as a 4 -wire system 4

Derivation of the dq 0 Equations of an Idealized Three -phase Synchronous Machine Axes of Reference Again axes of reference are chosen for each of the six windings. An axis of reference id developed along the direction of maximum positive mmf produced by each winding taken individually. Positive mmf is assumed to be directed across the gap from rotor to stator. Machine Equations- Phase Variables The stator and rotor voltages can be expressed in vector-matrix form as: Stator 5

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Rotor where, 6

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine In general, the flux linkages for any orientation of the rotor are: 7

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Stator Inductances The expressions for the inductances of the machine can be written down by plausibility arguments similar to those given in the book by Majmudar pages 224 - 234 and 408 – 415. Also, in the book by B. Adkins – pages 58 - 61. 8

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Stator – Rotor Mutual Inductances Stator Field Windings 9

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Stator Windings and dr windings 10

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Stator Windings and qr windings Rotor Inductances It may be noted that both the stator and rotor self and mutual inductances are constants independent of. 11

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Self Inductances Mutual Inductances 12

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Matrix Notation The following inductance matrices may be defined: Note that represents the leakage inductance due to the leakage flux. 13

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Transformation from phase quantities to dq 0 axes Field on the rotor The machine dynamic equations are: where, 14

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Matrices is: and are defined by (26), (27), (28) and (29). The matrix Observations: 1) The two circuits on the rotor, that is dr and qr, have resistances and selfinductances which are not necessarily equal. 2) The three stator circuits have identical resistances and self-inductances which are symmetrical. Hence, it may be possible to simplify the stator equations by a change in variable. 15

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine 3) It may be apparent that a transformation of variables to any reference frame other than a reference frame fixed on the rotor will result in the differential equations associated with these circuits to become more complicated rather than simplified. Transformation of Stator Variables to the dq 0 axes fixed on the rotor The dq 0 axes are fixed on the rotor (see Fig. 2) and they are rotating at angular velocity of. The stator variables as seen from dq 0 axes are: 16

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine where, for , the is: Since the rotor windings are rotating at rotor speed, the rotor variables do not need to be transformed. To transform equation (30) to the dq 0 s reference frame, first multiply this equation by. 17

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Using (35) and (36) in (39), we will have From equation (37), Note that 18

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine The equation (42) can be rewritten as: Since the rotor rotates at the same speed as the reference frame, the rotor equation remains unchanged. Transformation of the Stator Flux linkage Equation Multiplying (32) by , 19

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Note that The term The second term can be written as – can be written as: 20

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Homework problem show that equation (48) and (49) are correct. The stator flux equation is: which results in 21

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Transformation of the Rotor Flux linkage Equation to the d-q axes The rotor flux linkage equation is: Rewrite the above as Equation (55) can be written as 22

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine After hard labor, you may obtain the following: Using (56) and (29), is: 23

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine The scalar forms of (57) are: 24

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Summary of the Synchronous Machine Equations in the dq 0 reference frame rotating at rotor speed 25

Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine where, 26

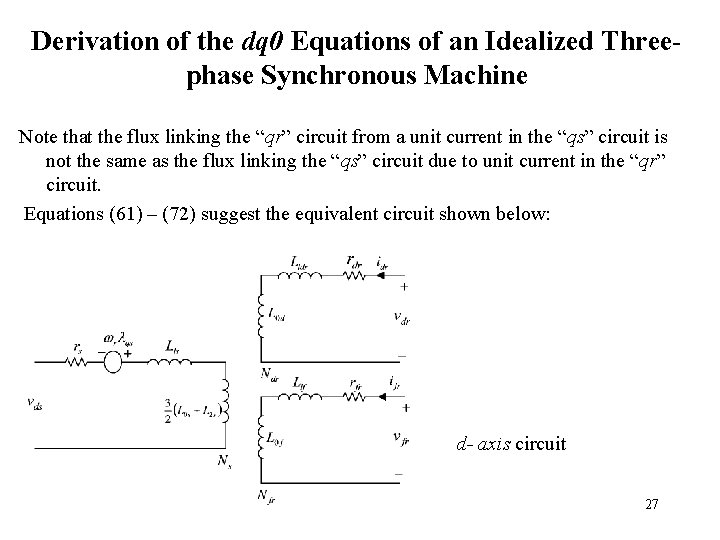
Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine Note that the flux linking the “qr” circuit from a unit current in the “qs” circuit is not the same as the flux linking the “qs” circuit due to unit current in the “qr” circuit. Equations (61) – (72) suggest the equivalent circuit shown below: d- axis circuit 27

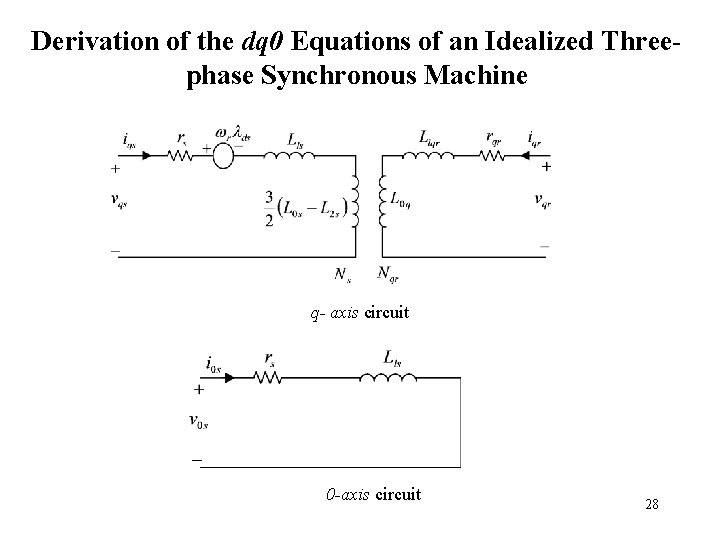
Derivation of the dq 0 Equations of an Idealized Threephase Synchronous Machine q- axis circuit 0 -axis circuit 28