Lecture 2 2 NP Class P NP PSPACE




































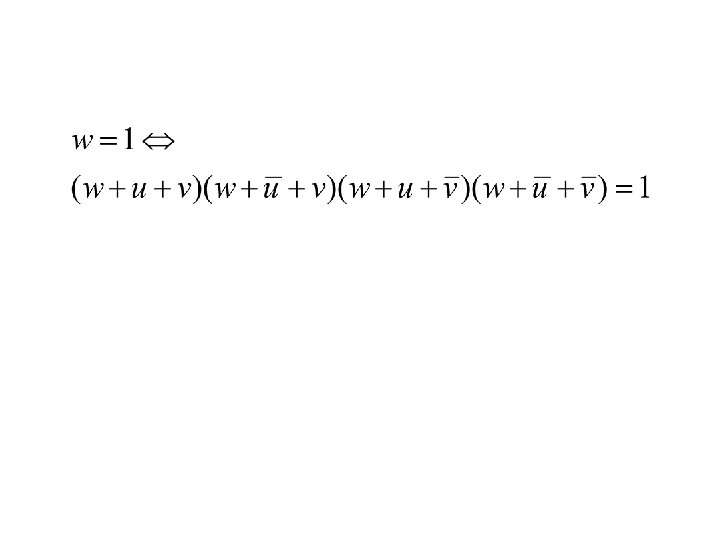








- Slides: 53

Lecture 2 -2 NP Class

P = ? NP = ? PSPACE • They are central problems in computational complexity.

Is it true that a problem belongs to NP iff its solution can be polynomial-time checkable ? Answer: No!

Integer Programming

Decision version of Integer Programming


How to prove a decision problem belonging to NP? How to design a polynomial-time nondeterministic algorithm?

Hamiltonian Cycle • Given a graph G, does G contain a Hamiltonian cycle? • Hamiltonian cycle is a cycle passing every vertex exactly once.

Post office

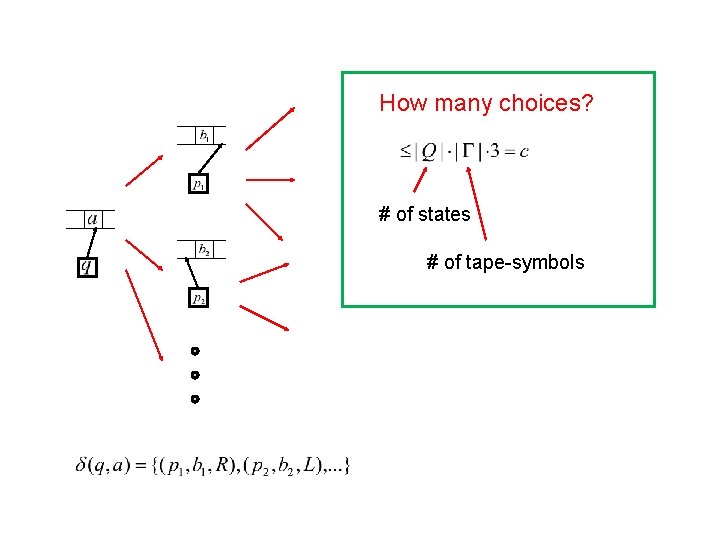
Nondeterministic Algorithm • Guess a permutation of all vertices. • Check whether this permutation gives a cycle. If yes, then algorithm halts. What is the running time?

How many choices? # of states # of tape-symbols

Minimum Spanning Tree • Given an edge-weighted graph G, find a spanning tree with minimum total weight. • Decision Version: Given an edge-weighted graph G and a positive integer k, does G contains a spanning tree with total weight < k.

Nondeterministic Algorithm • Guess a spanning tree T. • Check whether the total weight of T < k. This is not clear!

How to guess a spanning tree? • Guess n-1 edges where n is the number of vertices of G. • Check whether those n-1 edges form a connected spanning subgraph, i. e. , there is a path between every pair of vertices.

Co-decision version of MST • Given an edge-weighted graph G and a positive integer k, does G contain no spanning tree with total weight < k?

Algorithm • Computer a minimum spanning tree. • Check whether its weight > k. If yes, the algorithm halts.

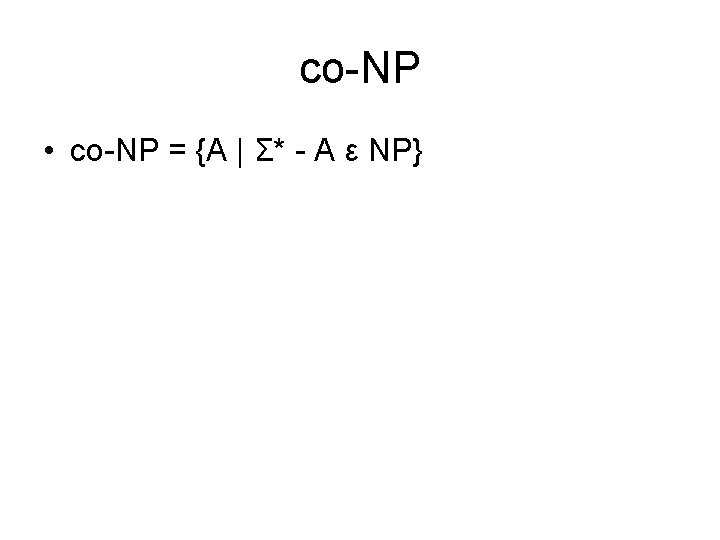
co-NP • co-NP = {A | Σ* - A ε NP}

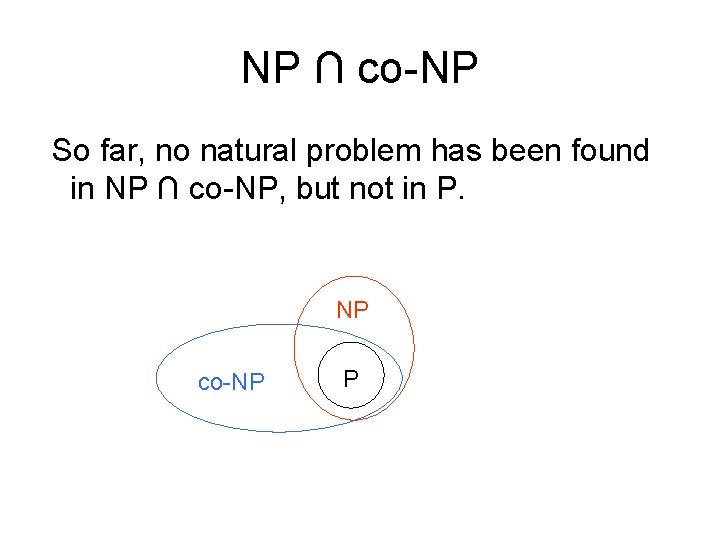
NP ∩ co-NP So far, no natural problem has been found in NP ∩ co-NP, but not in P. NP co-NP P

Linear Programming • Decision version: Given a system of linear inequality, does the system have a solution? • It was first proved in NP ∩ co-NP and later found in P (1979).

Primality Test • Given a natural number n, is n a prime? • It was first proved in NP ∩ co-NP and later found in P (2004).

Therefore • A natural problem belonging to NP ∩ co. NP is a big sign for the problem belonging to P.

Proving a problem in NP • In many cases, it is not hard. • In a few cases, it is not easy.

Integer Programming • Decision version: Given A and b, does Ax > b contains an integer solution? • The difficulty is that the domain of “guess” is too large.

Structure of NP

If P = NP, then P NP-complete

Ladner Theorem • If NP ≠ P, then there exists a set A lying between P and NP-complete class, i. e. , A is in NP, but not in P and not being NPcompete.

Polynomial-time many-one reduction

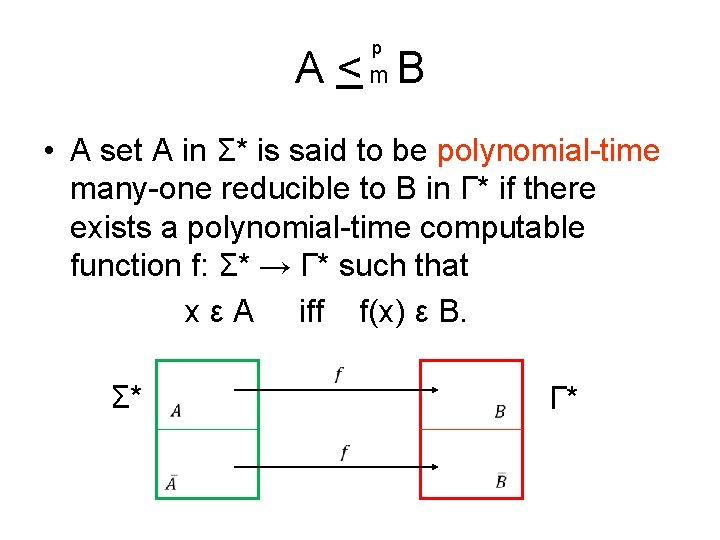
p A < m B • A set A in Σ* is said to be polynomial-time many-one reducible to B in Γ* if there exists a polynomial-time computable function f: Σ* → Γ* such that x ε A iff f(x) ε B. Σ* Γ*

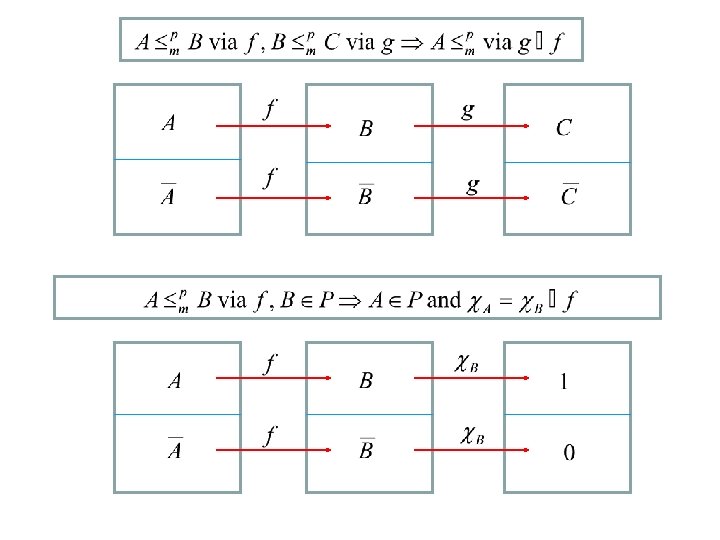
p Property of < m p m p m • A < B and B < C imply A < C p m • A < B and B ε P imply A ε P


A = Hamiltonian cycle (HC) • Given a graph G, does G contain a Hamiltonian cycle?

B = decision version of Traveling Salesman Problem (TSP) • Given n cities and a distance table between these n cities, find a tour (starting from a city and come back to start point passing through each city exactly once) with minimum total length. • Given n cities, a distance table and k > 0, does there exist a tour with total length < k?

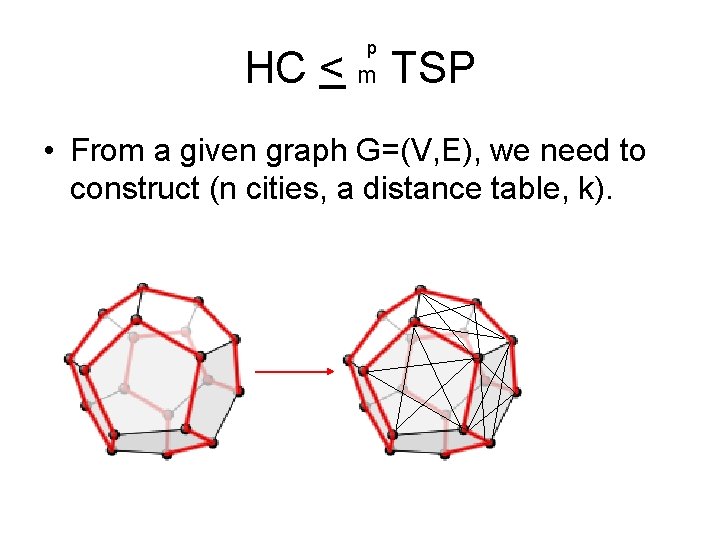
p HC < m TSP • From a given graph G=(V, E), we need to construct (n cities, a distance table, k).

p 3 -SAT < m SAT • SAT: Given a Boolean formula F, does F have a satisfied assignment? • An assignment is satisfied if it makes F =1. • 3 -SAT: Given a 3 -CNF F, does F have a satisfied assignment?

Boolean Algebra

Boolean Algebra

3 CNF

Examples


p SAT < m 3 -SAT • SAT: Given a Boolean formula F, does F have a satisfied assignment? • An assignment is satisfied if it makes F =1. • 3 -SAT: Given a 3 -CNF F, does F have a satisfied assignment?

Examples Not a polynomial-time reduction!!!


Examples

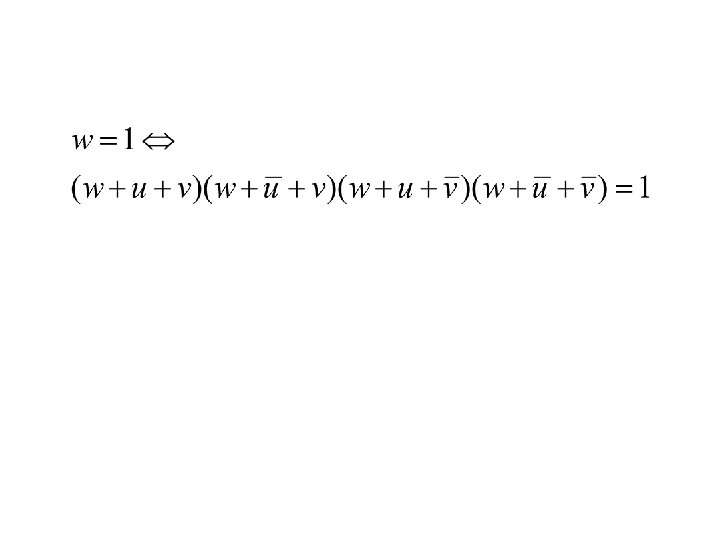

NP-complete • A set A is NP-hard if for any B in NP, p B < m A. • A set A is NP-complete if it is in NP and NP-hard. • A decision problem is NP-complete if its corresponding language is NP-complete. • An optimization problem is NP-hard if its decision version is NP-hard.

NP-hard in wide sense • A problem is said to be NP-hard in wide sense if following holds: • if it can be solved in polynomial-time, then P=NP (i. e. , all problems in NP can be solved in deterministic polynomial-time). • For example, the TSP is NP-hard in wide sense.

TSP is NP-hard • TSP can be solved in polynomial-time iff its decision version can be solved in polynomial-time. • The decision version of TSP is NPcomplete. • Hence, if TSP can be solved in polynomial -time, then NP=P.

Berman-Hartmanis Conjecture • All NP-complete sets are polynomial-time isomorphic to each other.

How many equivalence classes • Between any two equivalence classes, there is a new one. • Like rational numbers.

Characterization of NP


Thanks, end