Lecture 2 1 LOGIC AND PROOFS Discrete Mathematics

Lecture 2 1. LOGIC AND PROOFS Discrete Mathematics Dr. -Ing. Erwin Sitompul http: //zitompul. wordpress. com

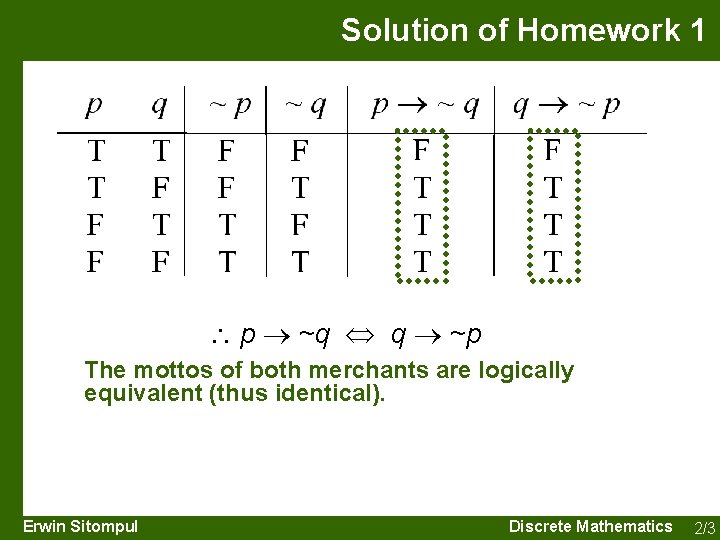
Solution of Homework 1 Two merchants publish new marketing campaign to attract more customers. The first merchant launches a motto “Good stuffs are not cheap”, while the second merchants says “Cheap stuffs are not good”. a) Examine whether both mottos tell the same message or not. b) In your opinion, which motto is better? Solution: Taking p: Good stuffs q: Cheap stuffs then the motto of the first merchant is p ~q And the one of the second merchant is q ~p p ~q q ~p Erwin Sitompul ? Discrete Mathematics 2/2

Solution of Homework 1 p ~q q ~p The mottos of both merchants are logically equivalent (thus identical). Erwin Sitompul Discrete Mathematics 2/3

Variances of Conditional Proposition Converse: q p Inverse: ~p ~q Contrapositive: ~q ~p Erwin Sitompul Discrete Mathematics 2/4

Variances of Conditional Proposition Example: Determine the converse, inverse, and contrapositive of: “If Amir owns a car, then he is rich. ” Solution: Converse “If Amir is rich, then he owns a car. ” Inverse: “If Amir does not own a car, then he is not reach. ” Contrapositive: “If Amir is not rich, then Amir does not own a car. ” Converse: q p Inverse: ~p ~q Contrapositive: ~q ~p Erwin Sitompul Discrete Mathematics 2/5

Contrapositive Example: Determine the contrapositive of the following propositions: a) “If she is found guilty, then she will be put in prison. ” b) “If 6 is greater than 0, then 6 is not a negative number. ” p only if q c) “Ivan passes the exam only if he studies hard. ” Solution: a) “If she is not put in prison, then she was not found guilty. ” b) “If 6 is a negative number, then 6 is not greater than 0. ” c) “If Ivan does not study hard, he does not pass the exam. ” Contrapositive: ~q ~p Erwin Sitompul Discrete Mathematics 2/6

Contrapositive Example: p only if q d) “Only if she is not late then she will get the job. ” e) “Wind is necessary for the kite to fly. ” q necessary for p f) “Rain falling in the afternoon is sufficient to p sufficient for q make the night freezing cold. Solution: d) “If she is late, then she will not get the job. ” e) “If the wind does not blow, then the kite cannot fly. ” f) “If the night is not freezing cold, then rain does not fall in the afternoon. ” Erwin Sitompul Discrete Mathematics 2/7

Bi-conditional (Bi-implication) • Proposition form: “p if and only if q” • Notation: p q (p q) (q p) Erwin Sitompul Discrete Mathematics 2/8

Bi-conditional (Bi-implication) The form, “p if and only if q” can also be written as “if p then q and if q then p” Erwin Sitompul Discrete Mathematics 2/9

Bi-conditional (Bi-implication) Various ways to express bi-implication p q: § § § p if and only if q. p is the necessary and sufficient condition for q. p is necessary and sufficient for q. if p then q, and conversely (vise versa). if p then q and if q then p. p iff q. Erwin Sitompul Discrete Mathematics 2/10

Bi-conditional (Bi-implication) Example: Bi-implication in various expressions § 1 + 1 = 2 if and only if 2 + 2 = 4. § The necessary and sufficient condition for rain to fall is high air humidity. § If you are rich, then you have much money, and vice versa. § Cikarang is located in West Java iff West Java is one of 33 provinces in Indonesia. § If the weather is hot then I buy ice cream, and if I buy ice cream then the weather is hot. Erwin Sitompul Discrete Mathematics 2/11

Bi-conditional (Bi-implication) Example: Bi-implication in various expressions § Training and discipline are sufficient and necessary for you to win the match. § You are promoted if you have connection, and you have connection if you are promoted. § If I watch television too much then my eyes are irritated, and vice versa. § Trains always come late when and only when I need them for travel. Erwin Sitompul Discrete Mathematics 2/12

Logical Laws for Implication and Bi-implication Erwin Sitompul Discrete Mathematics 2/13

Some Examples Example: Given a proposition “It is not true that he learns Technical Drawing but not State Philosophy. ”, a) Express the proposition above in symbolic notation (logical expression). b) Write a logically equivalent proposition as the proposition above (Hint: Use De Morgan’s Law). Solution: Taking p: He learns Technical Drawing. q: He learns State Philosophy. then: a) ~ (p ~q) b) ~ (p ~q) ~ p q “He does not learn Technical Drawing or indeed learns State Philosophy. ” Erwin Sitompul Discrete Mathematics 2/14

Some Examples Example: Three propositions are given to describe the quality of a hotel: p : The service is good. q : The room rate is low. r : The hotel is a three star hotel. Translate the following proposition into symbolic notation using p, q, and r : a) “The room rate is low but the service is bad. ” b) “Either the room rate is high or the service is good, but not both. ” c) “It is not true that if a hotel is a three star hotel, then the room rate is low and the service is bad. ” Solution: a) q ~p Erwin Sitompul b) ~q p (~q ~p ) (q p) c) ~ (r (q ~p)) Discrete Mathematics 2/15

Some Examples Example: Express the following statement in symbolic notation: “If you are below 17 years old, then you may not vote in a general election, unless you are already married. ” Solution: Defining: p : You are below 17 years old. q : You are already married. r : You may vote in a general election. then the statement above can be express in symbolic notation as: (p ~q) ~r “If you are below 17 years old and are not already married, then you may not vote in a general election. ” r (~p q) Erwin Sitompul Discrete Mathematics 2/16

Some Examples Example: Proof that [~p (p q)] q is a tautology. Solution: To proof the tautology, we construct the truth table: True in all cases [~p (p q)] q is a tautology. Erwin Sitompul Discrete Mathematics 2/17

Argument is a list of propositions written as: In this case, p 1, p 2, …, pn are denoted as hypothesis (premise) and q as conclusion (consequence) The value of an argument may be valid or invalid. It should be emphasized that valid does not necessarily means true. Erwin Sitompul Discrete Mathematics 2/18

Argument Definition: An argument is valid if the conclusion is true, then all the hypotheses are true; otherwise the argument is invalid. If an argument is true, then we can say “the conclusion logically follows the hypotheses; or equivalently showing that the implication: (p 1 p 2 pn) q is true. An invalid argument shows false reasoning. Erwin Sitompul Discrete Mathematics 2/19

Argument Example: Show that the argument below is valid: “If a low tide occurs after an underwater earthquake, then a tsunami is triggered. ” “A low tide occurs after an underwater earthquake. ” “Therefore, a tsunami is triggered. ” Solution: Assume: p : A low tide occurs after an underwater earthquake. q : A tsunami is triggered. then the argument can be written as: p q There are two ways to proof the validity of the argument, both using the truth table, and will be discussed now. Erwin Sitompul Discrete Mathematics 2/20

Argument 1 st way: Constructing the truth table of p, q, and p q, and analyzing case by case. : p q § If each case “If all hypotheses are true, then the conclusion is true” applies, then the argument is valid. § Let us check whether if hypotheses p q and p are true, then the conclusion q is also true. § See line 1: p q and p are true at the same time, and q in line 1 is also true. § The argument is v a l i d. Erwin Sitompul Discrete Mathematics 2/21

Argument 2 nd way: Showing that the truth table of [(p q) p] q is a tautology. If the compound proposition is a tautology, then the argument is valid. p q § The argument is v a l i d. Erwin Sitompul Discrete Mathematics 2/22

Argument Show that the reasoning of the following argument is false, or the argument is invalid: “If a low tide occurs after an underwater earthquake, then a tsunami is triggered. ” “A low tide occurs after an underwater earthquake. ” Solution: Assume: p : A low tide occurs after an underwater earthquake. q : A tsunami is triggered. p q q then the argument can be written as: p § See line 3. § Conclusion p is false, even though all the hypotheses are true. § Thus, the argument is i n v a l i d. Erwin Sitompul Discrete Mathematics 2/23

Homework 2 No. 1: Given the statement “A valid password is necessary for you to log on to the campus server. ” a) Express the statement above in the proposition form of “if p then q. ” b) Determine also the negation, converse, inverse, and contrapositive of the statement. No. 2: Check the validity of the argument below: “If 5 is less then 4, then 5 is not a prime number. ” “ 5 is not less then 4. ” “ 5 is a prime number. ” Erwin Sitompul Discrete Mathematics 2/24

Homework 2 New No. 1: Given the statement “If you want to register for consultation with our doctors, you only have to send an SMS to the number on this card. ” a) Express the statement above in the proposition form of “If p then q. ” b) Determine also the negation, converse, inverse, and contrapositive of the statement. No. 2: Check the validity of the argument below: “I will prepare the budget proposal only if you give an initial approval. ” “You do not give an initial approval. ” “I will prepare the budget proposal. ” Erwin Sitompul Discrete Mathematics 2/25