Lecture 19 Spherical Polar Coordinates Come to see

Lecture 19 Spherical Polar Coordinates Come to see me before the end of term • I’ve put more sample questions and answers in Phils Problems • Past exam papers • Have a look at homework 2 (due in on 15/12/08) Remember Phils Problems and your notes = everything http: //www. hep. shef. ac. uk/Phil/PHY 226. htm

Hints for Homework 2 You know that and that So if you had you must write In questions that ask you to prove an expression is a solution of an equation, simply stick the expression into the equation starting at the heart of the equation working outwards and show that the LHS = RHS. (see Q 25 of tutorial questions and corresponding answer at Phils Problems)

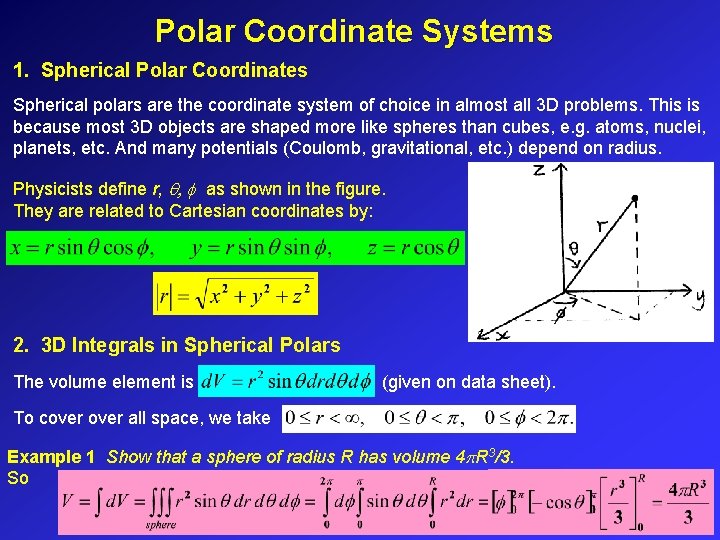
Polar Coordinate Systems 1. Spherical Polar Coordinates Spherical polars are the coordinate system of choice in almost all 3 D problems. This is because most 3 D objects are shaped more like spheres than cubes, e. g. atoms, nuclei, planets, etc. And many potentials (Coulomb, gravitational, etc. ) depend on radius. Physicists define r, q, f as shown in the figure. They are related to Cartesian coordinates by: . 2. 3 D Integrals in Spherical Polars The volume element is (given on data sheet). To cover all space, we take Example 1 Show that a sphere of radius R has volume 4 p. R 3/3. So

Polar Coordinate Systems Example 2 Find the Fourier transform of a screened Coulomb potential, As before we have the 3 D Fourier transform In this case f(r) is a function only of the magnitude of r and not its direction and so has perfect radial symmetry. Again the volume element is We therefore have There is a standard ‘trick’ which is to chose the direction of k to be parallel to the polar (z) axis for the integral. Then k. r becomes . Now clearly the whole integral is a function only of the magnitude of k, not its direction, i. e. F(k) becomes F(k):

Polar Coordinate Systems We therefore write so The integral over f is trivial: it just gives a factor of 2 p. involves r and q. Which integral should we do next? But note that the factor The presence of the together with the substitution the obvious choice: let So Rewrite makes integration by

Polar Coordinate Systems From previous page: We are then left with the integral over r: This type of integral was met earlier in the tutorial question exercises on Fourier transforms. It’s best to write the sine in terms of complex exponentials: This gives the final result:

Polar Coordinate Systems 3. 2 in Spherical Polars: Spherical Solutions As given on the data sheet, Example 3 Find spherically symmetric solutions of Laplace’s Equation 2 V(r) = 0. (Spherically symmetric’ means that V is a function of r but not of q or f. ) Therefore we can say Really useful bit!!!! If (as in the homework) we were given an expression for V(r) and had to prove that it was a solution to the Laplace equation, then we’d just stick it here and start working outwards until we found the LHS was zero. If on the other hand we have to find V(r) then we have to integrate out the expression.

Polar Coordinate Systems Multiplying both sides by r 2 gives Integrating both sides gives This rearranges to . where A is a constant. and so …. Integrating we get the general solution: We’ve just done Q 3(i) of the homework backwards!!! (see earlier note in red)

Polar Coordinate Systems 4. The Wave Equation in polar coordinates The wave equation is Let’s only look for spherically symmetric solutions Y(r, t), so the equation can be written As usual we look for solutions of the form As usual substitute this back in As usual separate the variables We equate both sides to a constant and since we expect LHO solutions this is -ve To make maths easier let this be

Polar Coordinate Systems giving The equation for T(t) is easy to solve Now we need to solve (*) This is tricky to solve …. . There is a standard trick which is to define , solve for u(r) and thus find R(r). Start by differentiating R(r) with respect to r using the product rule. Multiply both sides of the expression above by r 2 gives Now differentiate again.

Polar Coordinate Systems Therefore (*) Remember we originally needed to solve So equation (*) becomes: Thus we have solutions of the form: Remember and so And from the start of this example so

Polar Coordinate Systems Yet again I’ve made a mistake in the notes !!!!

Polar Coordinate Systems These are spherical waves moving in and out from the origin. Note the factor of 1/r. Intensity is related to amplitude squared. For waves moving out from the central point (origin). Our solution gives intensity as This is the well known inverse square law.