Lecture 18 SDH DWDM IP over SDH D

Lecture 18. SDH, DWDM, IP over SDH D. Moltchanov, TUT, Spring 2015

Outline SDH capacity and protection design SDH ring bandwidth design DWDM restoration design IP over SDH two-layers design

SDH: capacity design

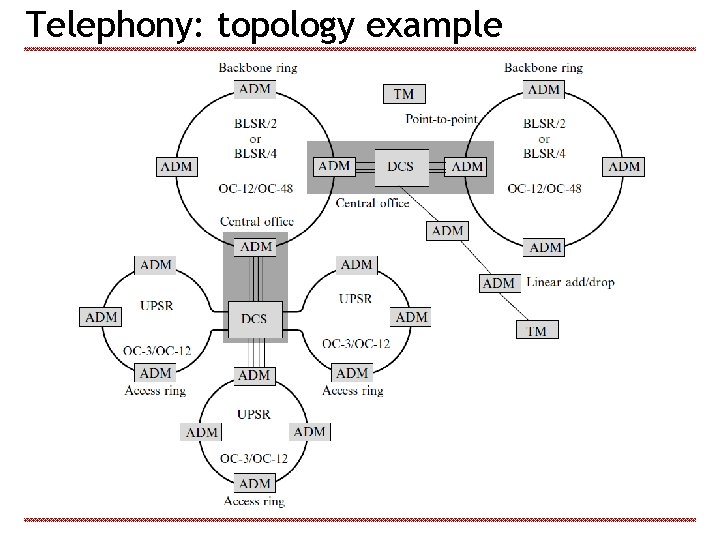
Telephony: routing of calls again Synchronous digital hierarchy (SDH) Replacement for PDH (E 1/E 3) Strictly synchronized (by atomic clocks) Allow for country wide networks Three types of nodes Terminal multiplexers (TM) Digital cross-connects (DCS) Add-drop multiplexers (ADM) Possible topologies Mesh: TM and DCS Ring: ADM nodes

Telephony: topology example

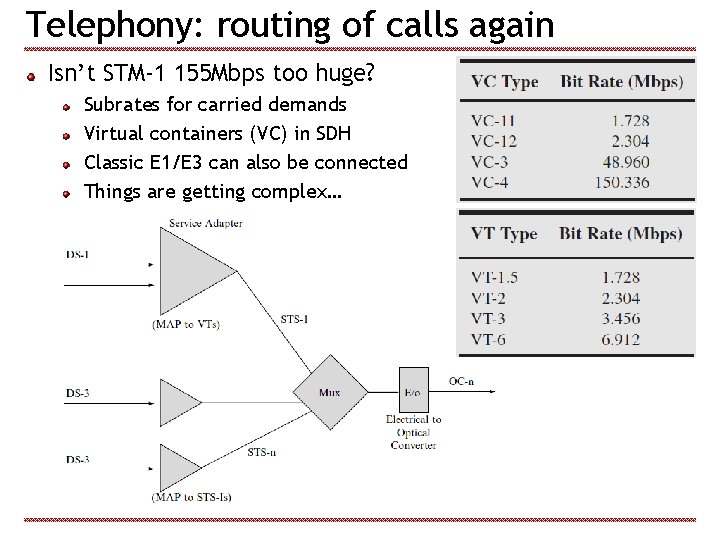
Telephony: routing of calls again Isn’t STM-1 155 Mbps too huge? Subrates for carried demands Virtual containers (VC) in SDH Classic E 1/E 3 can also be connected Things are getting complex…

Telephony: routing of calls again SONET/SDH are transport networks for Trunks from digital telephony networks (including cellular) Leased-line services Originally no support for IP networks IP: via Packet over SONET/SDH (Po. S) is very important nowadays Specifics designing SDH/SONET Analogous to those discussed previously More complicated: because of particular rates available Demand: usually subrate VC-12/VC-3/VC-4 Should be connected to a capable node Common assumptions Nodes are DSC capable Can switch as any rate: VC-12/VC-3/VC-4 for SDH

Telephony: routing of calls again Example 1: SDH as a transport for telephony 1 PDH E 1 (2. 048 Mbps) into 1 SDH VC-12 (2. 304 Mbps) Demands between ingress/egress DSCs in terms of VC-12 s A trunk group of 30 trunks (E 1) is a single demand for SDH 1 DVU = 1 VC 12 Available link rates STM-n: 1 – 155 – 622 Mbps, 16 – 2. 4 Gbps, 64 – 9. 9 Gbps STM-1: carries 63 VC-12 containers Capacity of a link measured in STM-1 (SDH) 1 LCU = 63 DVU (1 DVU – 1 E 1 converted into 1 VC-12, 30 trunks) 1 STM-1: 63 times 30 = 1890 calls… Should be a classic problem with modular design!

Telephony: routing of calls again The whole problem Minimize Subject to where are integers Note the following M = 63 and is the cost of one STM-1 unit on link e We optimize using flat cost for STM-1 We do not differentiate between costs of STM-1 within STM-n A problem can be extended…

Telephony: routing of calls again Let the cost of one STM-n on link e be The whole problem Minimize Subject to where are integers

SDH: restoration design

Telephony: SDH restoration What are the consequences of failure of a link? Loosing all the flows assigned to the path traversing link e i. e. to all the paths with coincidence coefficient surviving capacity of demand d in case of failure situation s simultaneous partial failure of several circuit groups d recall, demand volumes are in 30 trunks units What to do? How to minimize the effect? The capacities of circuit groups d should be split! Between as many non-zero flows as feasible This process is called path diversity Not commonly used in transport networks such as SDH… Why? ?

Telephony: SDH restoration One possible way Split each trunk group d to at least two flows How? Add a constraint What do we get applying this? Single link failures: availability is around 0. 5 for all demand volumes Even demand volumes: Odd demand volumes: at most slightly less than 0. 5 Path diversity in SDH Can be really costly Recall restoration example we considered! (245 instead of 85!) Here bundles are really large… Restores capacity of individual flows! Path diversity is also called path protection Another way: link protection Restores capacity of a link instead of individual flows

Telephony: SDH restoration Link protection Fixed link capacities assigned in normal state Minimizes the cost of additional link capacities For each link e there is a list of restoration paths Used when the link fails Capacity is restored using flows if link f belongs to path q restoring link e The whole problem Minimize Subject to where are integers

SDH: ring bandwidth design

Telephony: ring bandwidth design SONET/SDH two topologies Mesh: terminal multiplexers (TM) and digital cross-connects (DCS) Ring: add-drop multiplexers (ADM) nodes Why ring? Restoration mechanism Mesh: restoration via signaling between DCSs Ring: restoration is built-in… Restoration in rings: < 50 ms. for a single link failure ADM nodes Capable of inserting/extracting containers For example: we may insert or take out VC-12 at any ADM

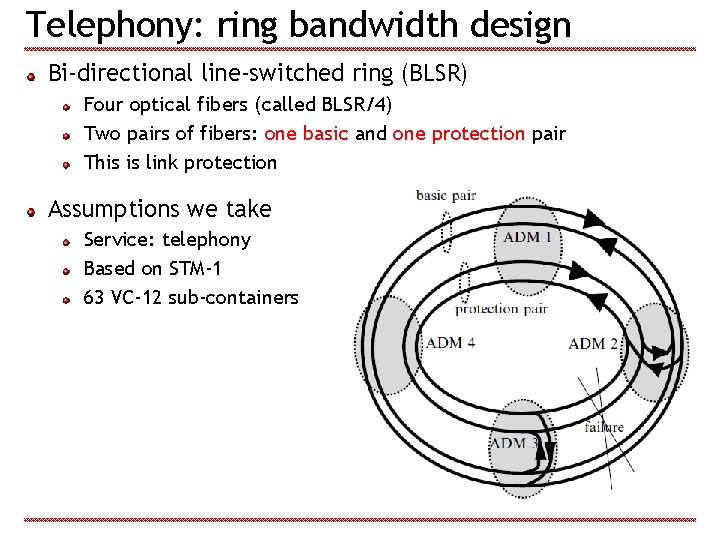
Telephony: ring bandwidth design Bi-directional line-switched ring (BLSR) Four optical fibers (called BLSR/4) Two pairs of fibers: one basic and one protection pair This is link protection Assumptions we take Service: telephony Based on STM-1 63 VC-12 sub-containers

Telephony: ring bandwidth design Problem Given the inherent SDH circular routing in ring topology and the demand volume, how do we determine what is the number and type of parallel rings needed? Example Demand d=1 between ADMs 1 and 2 has volume VC-12 s Three numbers out of {1, 2, …, 63} are reserved between 1 and 2 VC-12 s between them are used to realize 90 trunks If between ADMs 1 and 3 then reservation is on both segments When one segment fails then inner fiber is used Whole STM-1 is reswitched

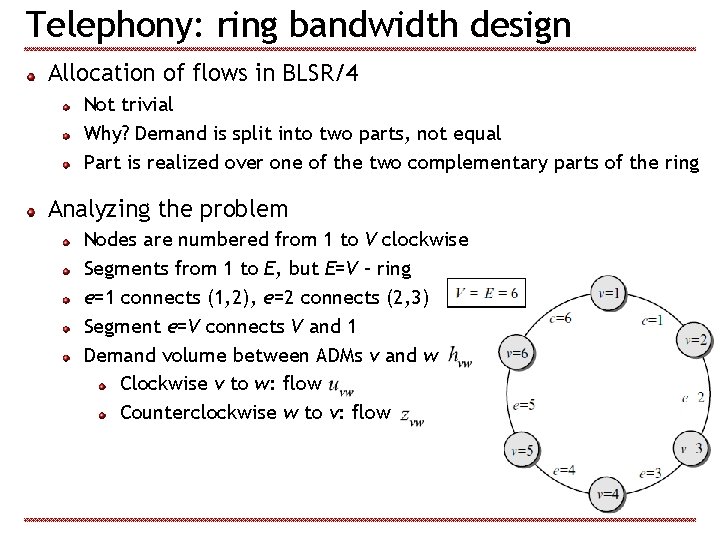
Telephony: ring bandwidth design Allocation of flows in BLSR/4 Not trivial Why? Demand is split into two parts, not equal Part is realized over one of the two complementary parts of the ring Analyzing the problem Nodes are numbered from 1 to V clockwise Segments from 1 to E, but E=V – ring e=1 connects (1, 2), e=2 connects (2, 3) Segment e=V connects V and 1 Demand volume between ADMs v and w Clockwise v to w: flow Counterclockwise w to v: flow

Telephony: ring bandwidth design Problem Minimize Subject to demand constraints and capacity constraints where are non-negative integers Link-incidence is now segment-demand incidence 1 if segment e belongs to clockwise path from v to w we did for M=63 (STM-1), can do for M=252 (STM-4) If segment is cut: inner fiber is used (protection switching) Another SDH ring: unidirectional path switched ring (UPRS) Restoration in UPSR: path protection

WDM: restoration

Telephony: WDM restoration Wavelength division multiplexing (WDM) What? Expanding capacity of fibers without installing new ones What? Bidirectional communication over a fiber How? Mx-ing number of optical carriers into a single fiber How? Using different wavelengths (AKA colors or lambdas) Development of WDM First published in 1978 Lab demonstration 1980 First WDM: two signals Now: up to 160, 10 Gbps -> 1. 6 Tbps Type of fibers Most WDM: single mode fiber 9 mkm Sometimes multimode fiber 50 -62. 5 mkm

Telephony: WDM restoration WDM systems Conventional WDM (CWDM): 8 channels in C band, 1550 nm Dense WDM (DWDM): denser spacing 40 channels at 100 GHz spacing or 80 at 50 GHz Ultra-dense WDM (UWDM): 12. 5 GHz spacing (320 channels) Units for dimensioning DVU: 10 Gbps (one wavelength, ~64 STM-1 modules) LCU: ~100 DVUs

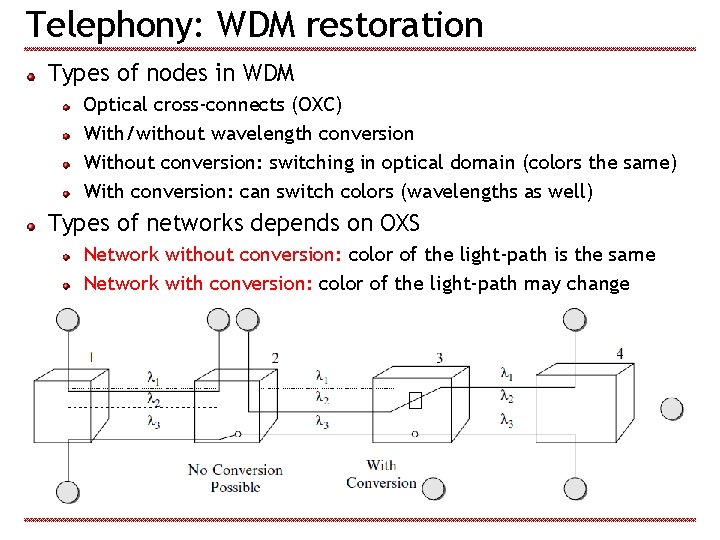
Telephony: WDM restoration Types of nodes in WDM Optical cross-connects (OXC) With/without wavelength conversion Without conversion: switching in optical domain (colors the same) With conversion: can switch colors (wavelengths as well) Types of networks depends on OXS Network without conversion: color of the light-path is the same Network with conversion: color of the light-path may change

Telephony: WDM restoration Problem Wavelength assignment problem: assign wavelength in optimal way assuming WDM network with path diversity, routing, and without wavelength conversion. Specifiyng the problem Demands to be realized Candidate path for demand d: Links (composed of sets of fibers) Colors (wavelength) available on links are labeled We include failures Failure situations State implies no links are broken At most one link at a time

Telephony: WDM restoration Analyzing the problem Volume of demand d realized in failure situation s number of light paths Cost of one LCU (optical fiber) on link e: Link failure coefficients 0: if link e is failed in situation s Link-path incidence: 1: if link e belongs to path p realizing demand d Path failure coefficients 0: if path p of demand d failed in situation s We have

Telephony: WDM restoration Number of light paths realizing d in color c of path p: Number of times color c is used on link e: Capacity of link e: The problem (OXCs without conversion) Minimize: Subject to: in each state s surviving flows realize DVUs for all demands d number of times color c is used on e fibers sufficient to realize demand for each color on all links where are non-negative integers

Telephony: WDM restoration Notes about the problem Integer programming: a lot of integer variables Complex to solve for large networks LP relaxation Make all variables continuous Allows to get approximate solutions What if OXCs with wavelength conversions? Becomes way simpler We get a “normal” switching network Identical to what we considered for SDH previously… Can be extended to include link opening costs

IP over SONET (Po. S)

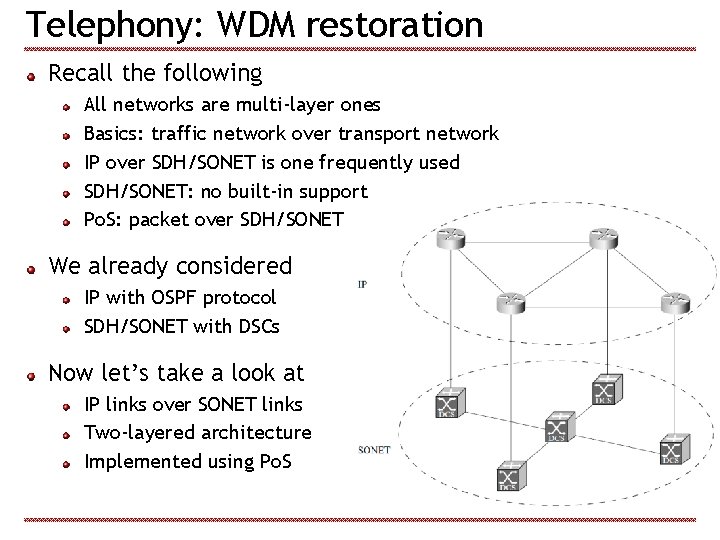
Telephony: WDM restoration Recall the following All networks are multi-layer ones Basics: traffic network over transport network IP over SDH/SONET is one frequently used SDH/SONET: no built-in support Po. S: packet over SDH/SONET We already considered IP with OSPF protocol SDH/SONET with DSCs Now let’s take a look at IP links over SONET links Two-layered architecture Implemented using Po. S

Telephony: WDM restoration Problem statement Given an IP intra-network domain and the fact that IP links are realized as transmission paths over a capacitated SONET, how do we determine capacity required for the IP links and the routing of these links in SONET to minimize IP network cost. Want to work with SDH? Just replace capacities… When SONET and IP are owned by the same entity When owned by different entities (we one needs from SONET) Specifying the IP layer SONET network is given (nodes/capacities, etc. ) We are given IP traffic demands d=1, 2, …, D We are using OC-3 line cards (155. 52 Mbps) IP links are then modular multipliers of 155. 52 Mbps If demand < 155. 52 then IP link module value is M=155. 52

Telephony: WDM restoration Specifying the SONET layer IP links capacity is demand for SONET 1 DVU at SONET layer: 1 OC-3 (155. 52 Mbps) OC-3 demands are routed using OC-48 (2. 4 G) or OC-192 (9. 9 G) 1 LCU at SONET layer: N = 16 M (16 OC-3 in OC-48) Path in SONET: several DCSs End IP routers are mapped to some DSCs Example of demands 1 Mbps between two nodes in IP Becomes 1 LCU in IP that is equal to M=155. 52 Mbps (OC-3) 1 LCU in IP becomes 1 DVU in SONET (OC-3) 1 LCU in SONET OC-48: N=2. 4 Gbps 1 Mbps -> 155. 52 Mbps -> 2. 4 Gbps

Telephony: WDM restoration SONET IP Formalization of the problem IP network with V nodes and E links IP network traffic demands: Allowable paths for demand d: Link weights system: Flows induced by the weight system: IP link incidence coefficients: if path p of demand d uses e let modular capacity of link e in IP be (unknown, in modules of M) link capacities are demands to SONET network links in SONET: Link capacities in SONET: candidate path in SONET for IP link (demand) e: SONET link-incidence : if path q of demand e uses link g Notes on routing: Routing IP: dynamic, Routing SONET: semi-permanent

Telephony: WDM restoration Variables for optimization Link weights: IP link modular capacities: SONET modular capacities: Problem Minimize Subject to: IP link termination cost (cost of OC-3 cards at the end of link e, often linkindependent, ) Cost of routing in SONET non-negative integers Utilization to minimize congestion

Telephony: WDM restoration Cost of routing in SONET Setting ? Maximizing the spare capacity of SONET links Setting Cost rate (per month, per year) of one LCU of IP link e To be paid by IP provider to SONET operator The problem is a huge headache… LP relaxation? . . .