Lecture 18 OUTLINE Continue small signal analysis Logic

Lecture #18 OUTLINE • Continue small signal analysis • Logic functions • NMOS logic gates • The CMOS inverter Reading • Rabaey et al. : Chapter 5. 2 • Hambley: Chapter 7. 1 -7. 2 EECS 40, Spring 2004 Lecture 18, Slide 1 Prof. Sanders

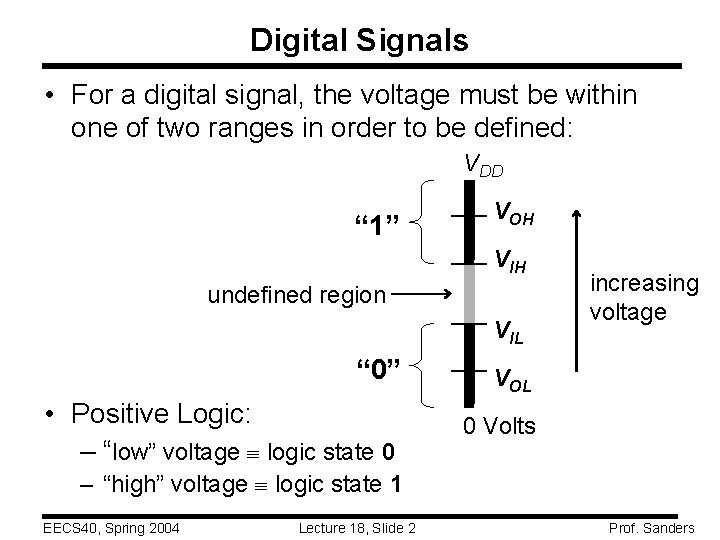
Digital Signals • For a digital signal, the voltage must be within one of two ranges in order to be defined: VDD “ 1” VOH VIH undefined region VIL “ 0” VOL • Positive Logic: – “low” voltage logic state 0 0 Volts increasing voltage – “high” voltage logic state 1 EECS 40, Spring 2004 Lecture 18, Slide 2 Prof. Sanders

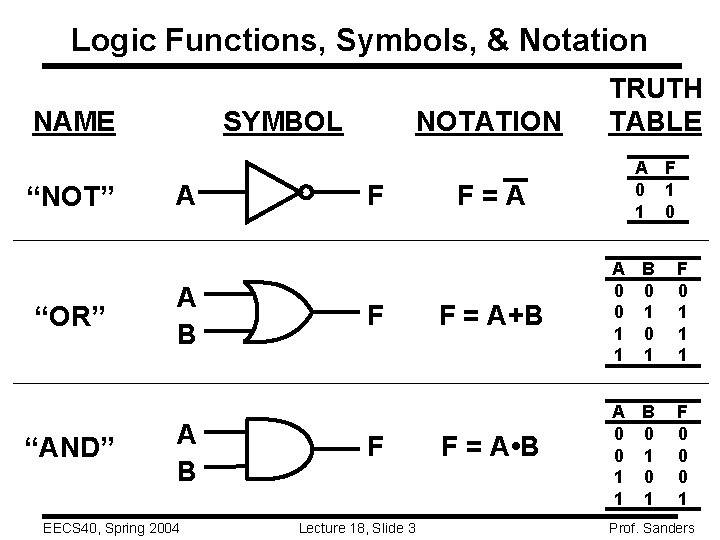
Logic Functions, Symbols, & Notation NAME “NOT” “OR” “AND” SYMBOL A A B EECS 40, Spring 2004 NOTATION F F F Lecture 18, Slide 3 F=A TRUTH TABLE A F 0 1 1 0 F = A+B A B 0 0 0 1 1 F 0 1 1 1 F = A • B A B 0 0 0 1 1 F 0 0 0 1 Prof. Sanders

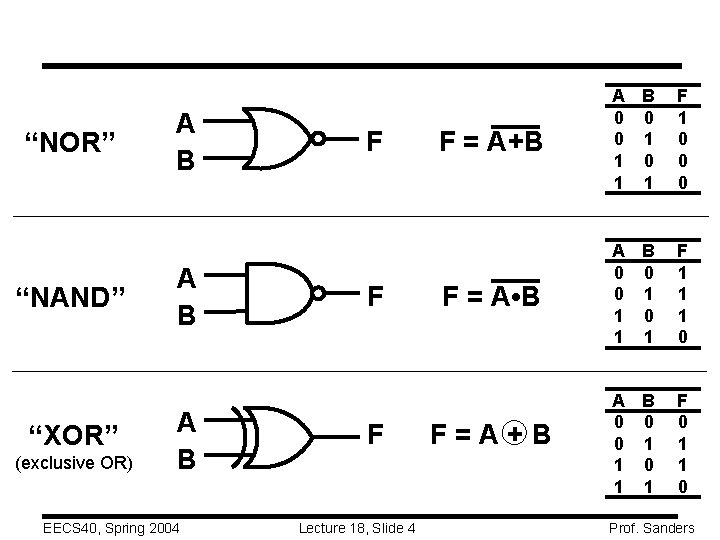
“NOR” “NAND” “XOR” (exclusive OR) A B A B EECS 40, Spring 2004 F F F Lecture 18, Slide 4 F = A+B A B 0 0 0 1 1 F 1 0 0 0 F = A • B A B 0 0 0 1 1 F 1 1 1 0 F=A+B A B 0 0 0 1 1 F 0 1 1 0 Prof. Sanders

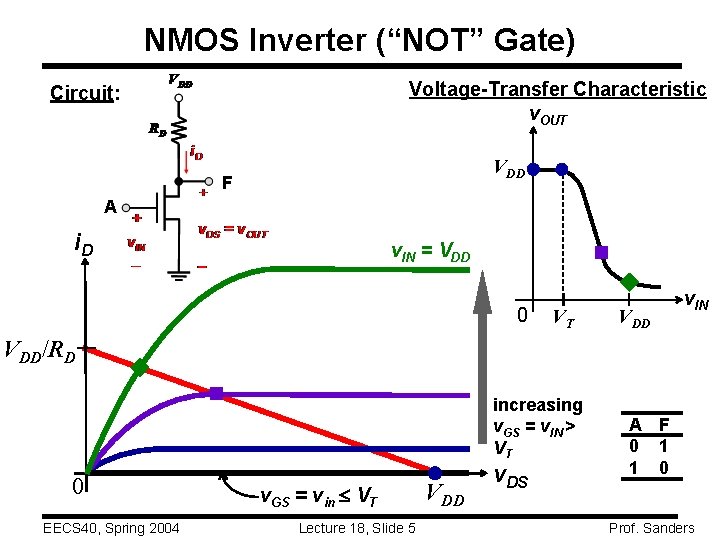
NMOS Inverter (“NOT” Gate) Voltage-Transfer Characteristic v. OUT Circuit: VDD F A i. D v. IN = VDD 0 VT VDD v. IN VDD/RD increasing v. GS = v. IN > VT 0 EECS 40, Spring 2004 v. GS = vin VT Lecture 18, Slide 5 VDD v. DS A F 0 1 1 0 Prof. Sanders

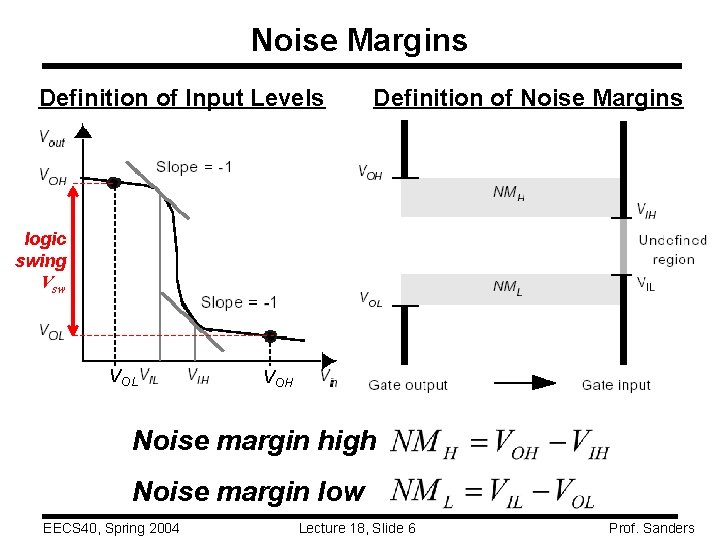
Noise Margins Definition of Input Levels Definition of Noise Margins logic swing Vsw VOL VOH Noise margin high Noise margin low EECS 40, Spring 2004 Lecture 18, Slide 6 Prof. Sanders

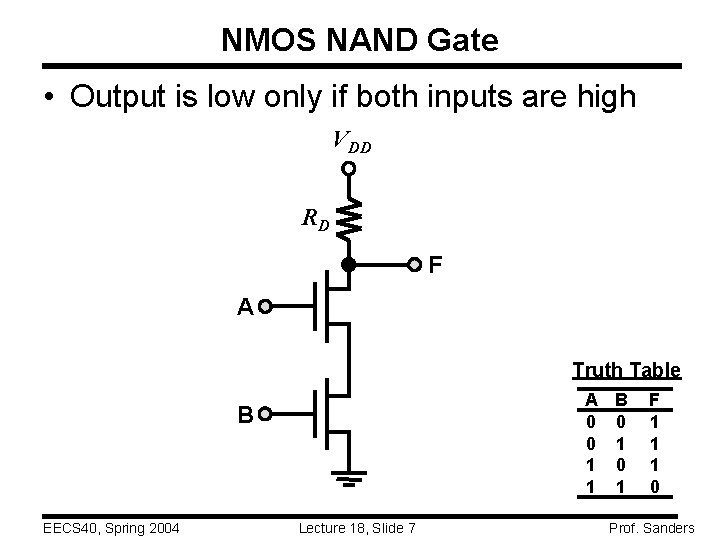
NMOS NAND Gate • Output is low only if both inputs are high VDD RD F A Truth Table A B 0 0 0 1 1 B EECS 40, Spring 2004 Lecture 18, Slide 7 F 1 1 1 0 Prof. Sanders

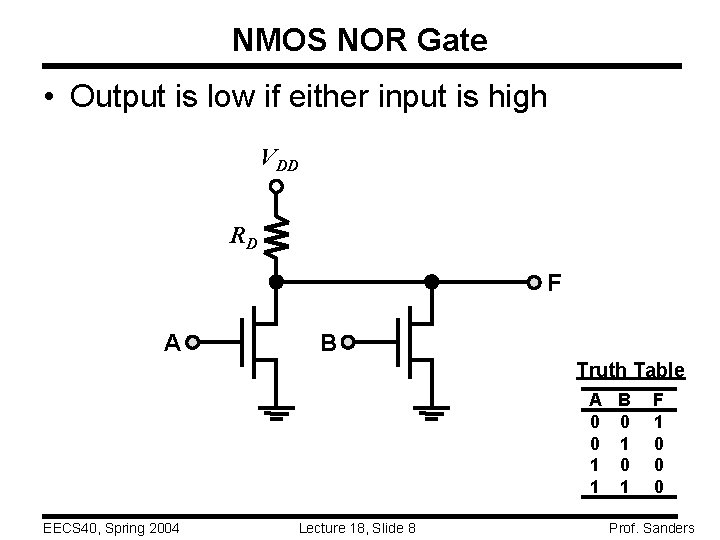
NMOS NOR Gate • Output is low if either input is high VDD RD F A B Truth Table A B 0 0 0 1 1 EECS 40, Spring 2004 Lecture 18, Slide 8 F 1 0 0 0 Prof. Sanders

Disadvantages of NMOS Logic Gates • Large values of RD are required in order to – achieve a low value of VOL – keep power consumption low à Large resistors are needed, but these take up a lot of space. • One solution is to replace the resistor with an NMOSFET that is always on. EECS 40, Spring 2004 Lecture 18, Slide 9 Prof. Sanders

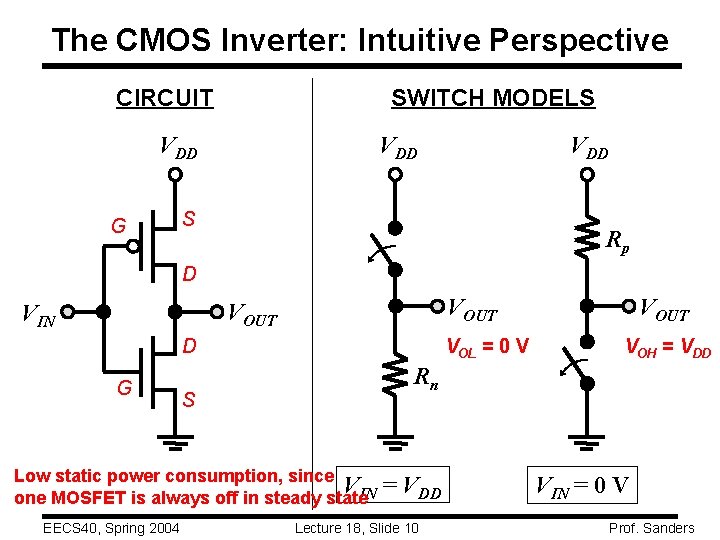
The CMOS Inverter: Intuitive Perspective SWITCH MODELS CIRCUIT VDD G VDD S Rp D VOUT VIN D G VOL = 0 V VOH = VDD Rn S Low static power consumption, since V one MOSFET is always off in steady state. IN EECS 40, Spring 2004 VOUT = VDD Lecture 18, Slide 10 VIN = 0 V Prof. Sanders

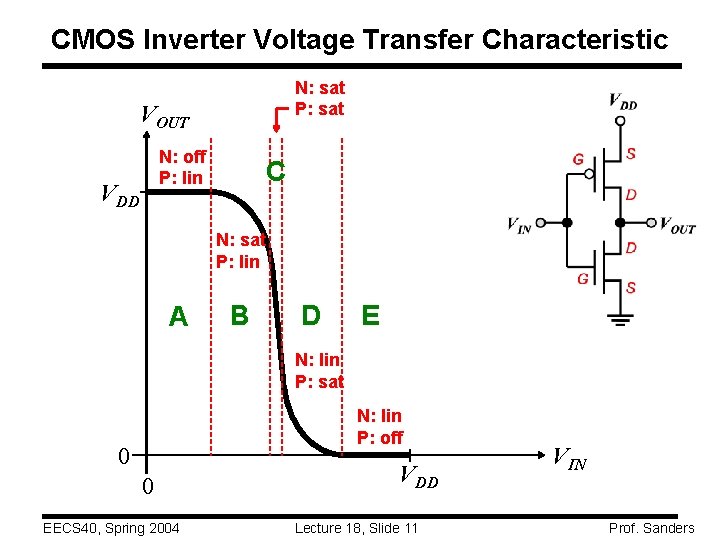
CMOS Inverter Voltage Transfer Characteristic N: sat P: sat VOUT N: off P: lin VDD C N: sat P: lin A B D E N: lin P: sat N: lin P: off 0 0 EECS 40, Spring 2004 VDD Lecture 18, Slide 11 VIN Prof. Sanders

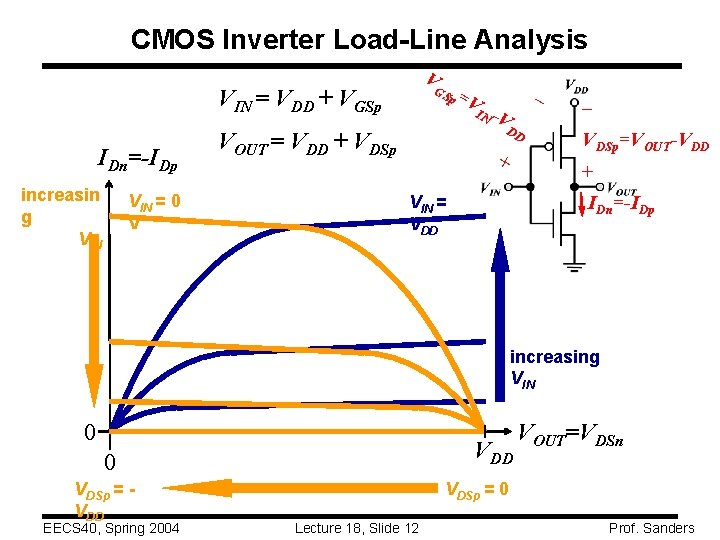
CMOS Inverter Load-Line Analysis V GS VIN = VDD + VGSp IDn=-IDp increasin g VIN = 0 V p =V IN - V DD VOUT = VDD + VDSp + – – VDSp=VOUT-VDD + IDn=-IDp VIN = VDD increasing VIN 0 VDD 0 VDSp = VDD EECS 40, Spring 2004 VOUT=VDSn VDSp = 0 Lecture 18, Slide 12 Prof. Sanders

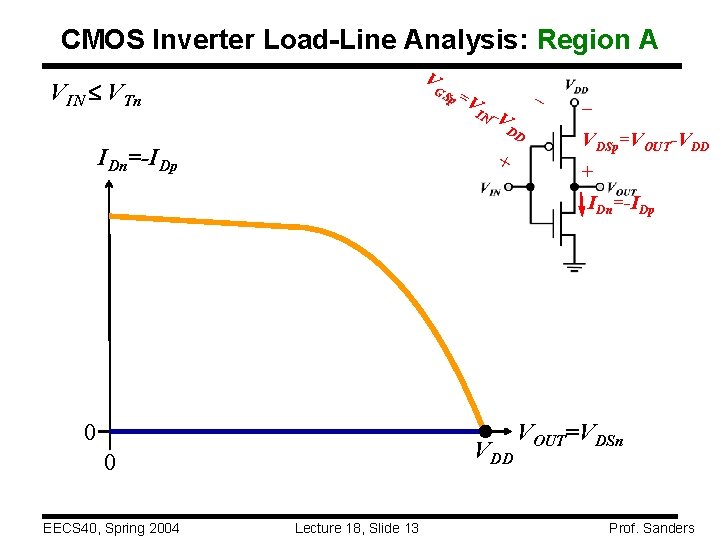
CMOS Inverter Load-Line Analysis: Region A V VIN VTn GS IDn=-IDp p =V IN - V DD + – – VDSp=VOUT-VDD + IDn=-IDp 0 VDD 0 EECS 40, Spring 2004 Lecture 18, Slide 13 VOUT=VDSn Prof. Sanders

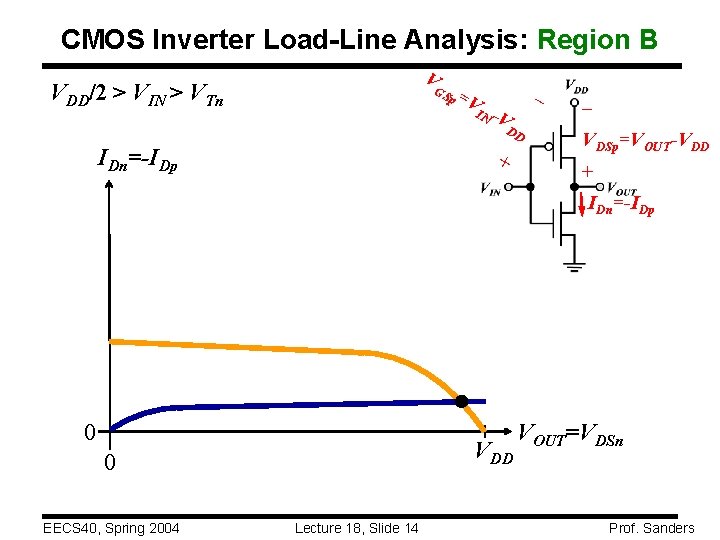
CMOS Inverter Load-Line Analysis: Region B V VDD/2 > VIN > VTn GS IDn=-IDp p =V IN - V DD + – – VDSp=VOUT-VDD + IDn=-IDp 0 VDD 0 EECS 40, Spring 2004 Lecture 18, Slide 14 VOUT=VDSn Prof. Sanders

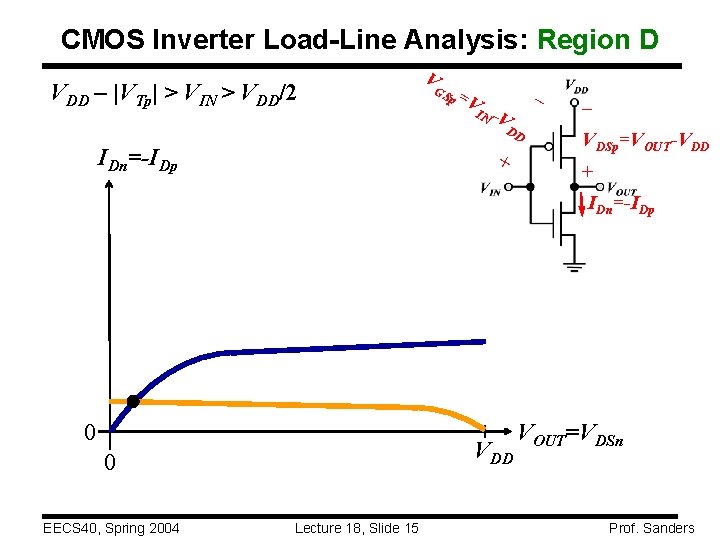
CMOS Inverter Load-Line Analysis: Region D VDD – |VTp| > VIN > VDD/2 IDn=-IDp V GS p =V IN - V DD + – – VDSp=VOUT-VDD + IDn=-IDp 0 VDD 0 EECS 40, Spring 2004 Lecture 18, Slide 15 VOUT=VDSn Prof. Sanders

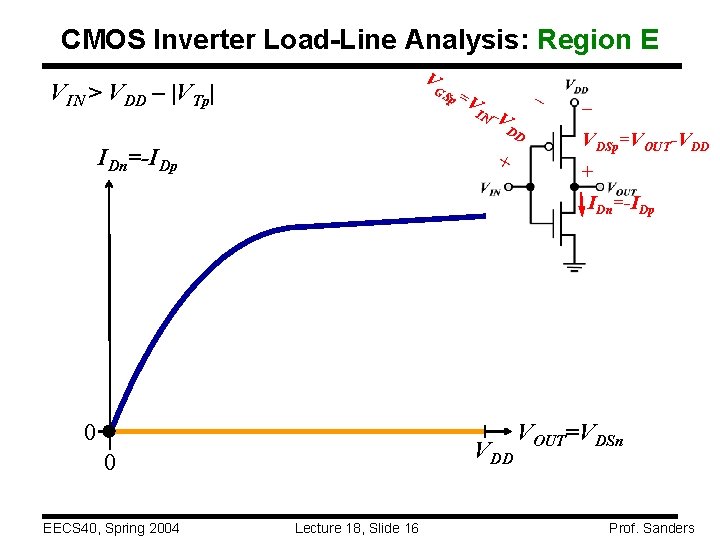
CMOS Inverter Load-Line Analysis: Region E V VIN > VDD – |VTp| GS IDn=-IDp p =V IN - V DD + – – VDSp=VOUT-VDD + IDn=-IDp 0 VDD 0 EECS 40, Spring 2004 Lecture 18, Slide 16 VOUT=VDSn Prof. Sanders