Lecture 18 Linear Program Algorithms Dual LP Strong

Lecture 18 Linear Program Algorithms

Dual LP • Strong Duality: The two LP has the same optimal value. The dual of dual LP is the primal LP.

Primal and Dual Optimal Solution: x = (4, 3, 0) Optimal Solution: y = (2. 5, 0, 0. 5) Observation: If a primal constraint is not tight, then the dual variable is 0.

LP algorithms • Given a linear program, how do we find its optimal solution? • Many different algorithms • Simplex • Ellipsoid • Interior Point

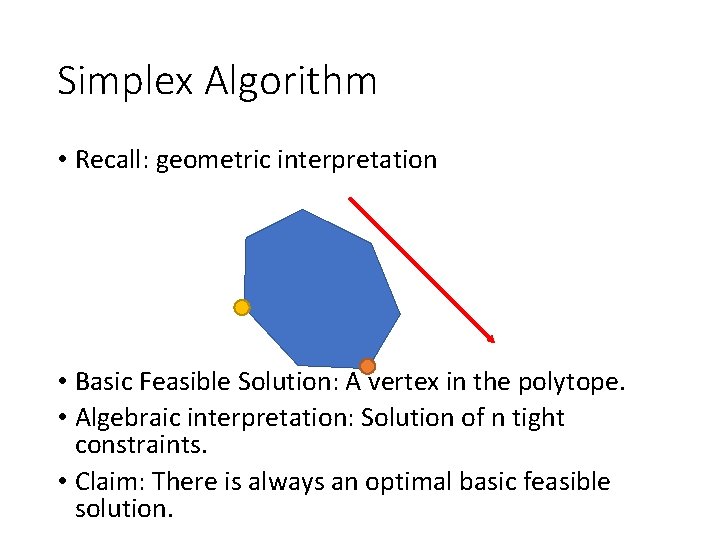
Simplex Algorithm • Recall: geometric interpretation • Basic Feasible Solution: A vertex in the polytope. • Algebraic interpretation: Solution of n tight constraints. • Claim: There is always an optimal basic feasible solution.

Simplex Algorithm [Dantzig 1947] • Idea: Start from a basic feasible solution, follow an edge in the polytope. • Algorithmically: follow an edge swap a constraint. • Many ways to decide which constraint to swap.

Running time of Simplex algorithm • Each move takes polynomial time, but how many moves do we need? • In the worst case can require 2 n moves. • But in practice simplex is often very fast! • Still used in many LP solvers.

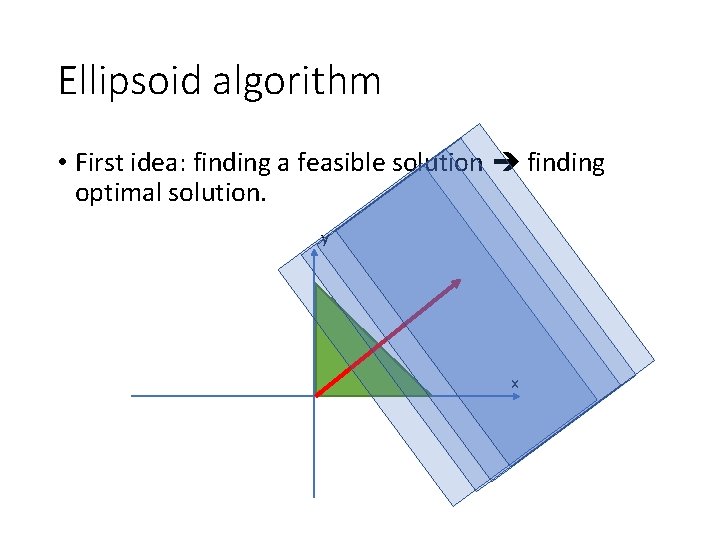
Ellipsoid algorithm • First idea: finding a feasible solution finding optimal solution. y x

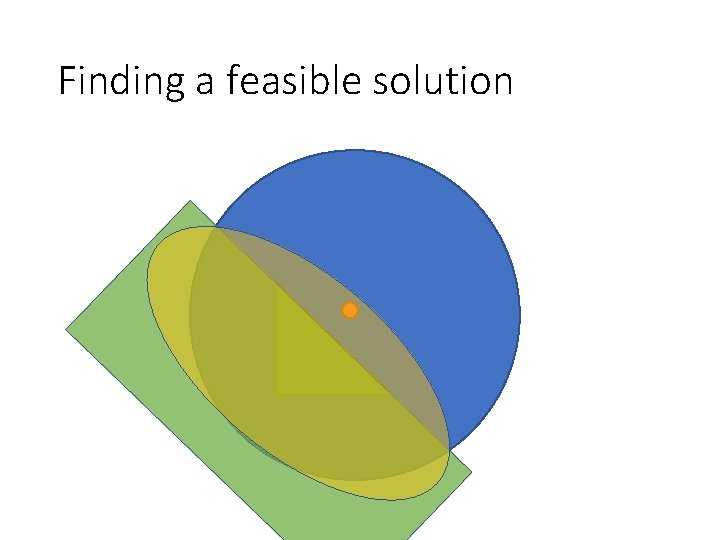
Finding a feasible solution

Running time of ellipsoid • Polynomial in the number of variables and constraints. • Actual running time is a bit slow, often used for low dimensional problems.

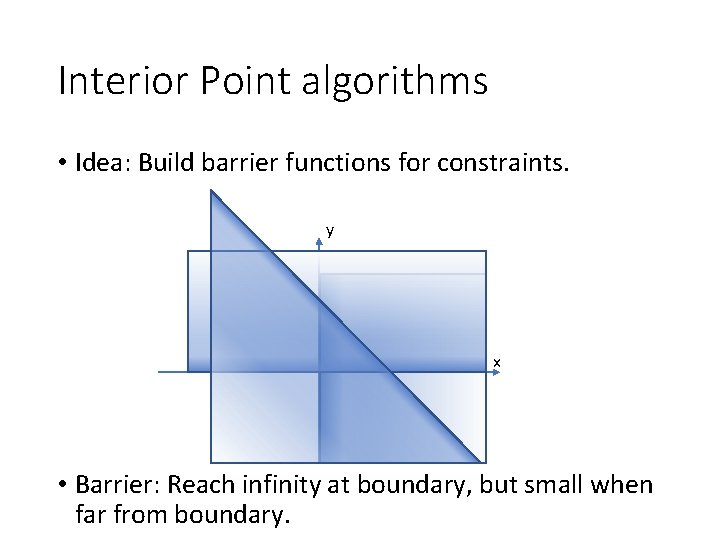
Interior Point algorithms • Idea: Build barrier functions for constraints. y x • Barrier: Reach infinity at boundary, but small when far from boundary.

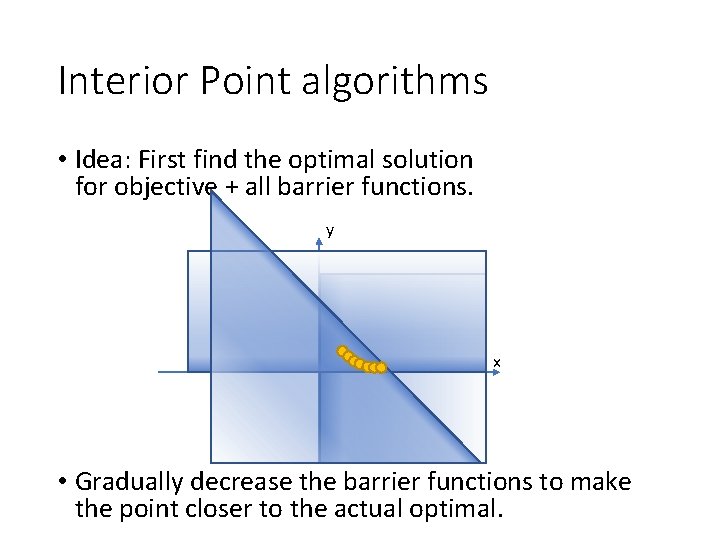
Interior Point algorithms • Idea: First find the optimal solution for objective + all barrier functions. y x • Gradually decrease the barrier functions to make the point closer to the actual optimal.

Running time for Interior point • Also polynomial in number of variables and constraints. • Can be implemented efficiently in practice. • Many recent developments in both theory and practice, becoming the method of choice in many LP solvers.