Lecture 18 CS 1813 Discrete Mathematics Loops Without

Lecture 18 CS 1813 – Discrete Mathematics Loops Without Invariants Are Like Disneyland Without Crowd Control 1

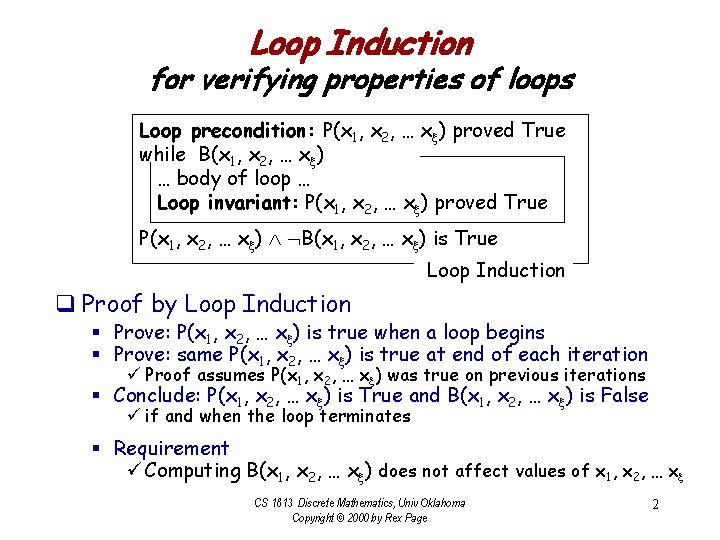
Loop Induction for verifying properties of loops Loop precondition: P(x 1, x 2, … xx) proved True while B(x 1, x 2, … xx) … body of loop … Loop invariant: P(x 1, x 2, … xx) proved True P(x 1, x 2, … xx) B(x 1, x 2, … xx) is True Loop Induction q Proof by Loop Induction § Prove: P(x 1, x 2, … xx) is true when a loop begins § Prove: same P(x 1, x 2, … xx) is true at end of each iteration ü Proof assumes P(x 1, x 2, … xx) was true on previous iterations § Conclude: P(x 1, x 2, … xx) is True and B(x 1, x 2, … xx) is False ü if and when the loop terminates § Requirement ü Computing B(x 1, x 2, … xx) does not affect values of x 1, x 2, … xx CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 2

sum = foldr (+) 0 — as a loop Function precondition: a[1. . n] defined integer sum(integer a[ ]) integer n = length(a[ ]) integer k, s k s=0 s = a[i] Conclude k=0 k at return i=1 Loop precondition: s = a[i] (by loop induction) i=1 while (k n) k = k+1 But what is k at return? s = s + a[k] k Loop terminates with k = n Loop invariant: s = a[i] i=1 by counting-loop theorem return s (coming up) § Loop precondition True ü Subscript set for is empty and empty sums are 0, by convention § Loop invariant True at end of loop if True at beginning k+1 k a[i] = a[k+1] + a[i] where k denotes top-of-loop value of k i=1 CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 3

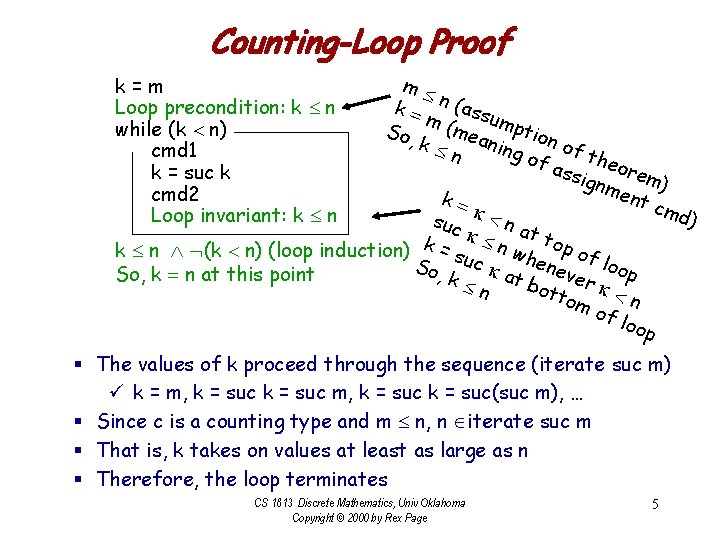
The Counting-Loop Theorem q A type, c, is a “counting type” if § c includes operations suc: : c -> c and ( ), (=): : c -> bool § (suc m) n whenever (m n) {Note: x y means (x y) (x = y)} § (m n) (n iterate suc m) ü iterate f x = x : (iterate f (f x)) ü Computation pattern: iterate f x = [x, f(f x), f(f(f x), … ] q Theorem (counting loop) § If k, m, n : : c, and m n, and § If neither cmd 1 nor cmd 2 affects the values of k, m, or n § Then the following loop terminates and when it does, k = n k=m while (k n) cmd 1 k = suc k cmd 2 CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 4

Counting-Loop Proof m k = n (ass u m( mea mptio So, k ning n of a theo re ssig nme m) nt c k= md) suc k n a t to k k k n (k n) (loop induction) = su n wh p of ene ck loop S o , v So, k = n at this point a e k tb ott r k n om n of l oop k=m Loop precondition: k n while (k n) cmd 1 k = suc k cmd 2 Loop invariant: k n § The values of k proceed through the sequence (iterate suc m) ü k = m, k = suc(suc m), … § Since c is a counting type and m n, n iterate suc m § That is, k takes on values at least as large as n § Therefore, the loop terminates CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 5

add. Vectors = zip. With (+) Function precondition: x[1. . n], y[1. . n] defined bool vector. Sum(double x[ ], double y[ ]) integer k, n = length(x[ ]) double z[1. . n] k=0 Loop precondition: i k. z[i] = x[i] + y[i] while (k n) k = k+1 z[k] = x[k] + y[k] Loop invariant: i k. z[i] = x[i] + y[i] return z[1. . n] By loop induction, ( i k. z[i] = x[i] + y[i]) By counting-loop theorem, k = n Since k = n, i n. z[i] = x[i] + y[i] That is, z[i] = x[i] + y[i] for i = 1, 2, … n CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 6

or = foldr (/) False — as a loop Function precondition: a[1. . n] defined, a[n+1] exists bool or(bool a[ ], integer n) integer k a[n+1] = True k=1 Loop precondition: i k. a[i] while (not a[k]) k = k+1 Loop invariant: i k. a[i] return (k n) § Conclude: ( i k. a[i]) a[k] at return ü by loop induction § Case 1: k n at return ü (a[k] = True) (k n) n ü So, ( a[i] ) = True = (k n) § Case 2: k n at return ü i k. a[i] ü i n+1. a[i] ü i n. a[i] i=1 CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page ü a[i] = False = (k n) n i=1 7

Is NOT palindrome is. Palindrome xs = (xs == reverse xs) Function precondition: a[1. . n] defined Palindromic predicates ü i n div 2. a[i] = a[n-i+1] bool is. Palindrome(char a[ ]) ü ( i. a[i] a[n-i+1]) integer k, n = length(a[ ]) bool ok. So. Far = True What proves this k=1 equation is True? Loop precondition: ( i k. a[i] = a[n-i+1]) = ok. So. Far loop induction while (ok. So. Far (k n div 2)) ok. So. Far = (a[k] = a[n-k+1] ) k = k+1 Loop invariant: ( i k. a[i] = a[n-i+1]) = ok. So. Far return ok. So. Far (k n div 2) (a[k] = a[n-k+1] ) If True, then If False, then (k n div 2) (a[k] = a[n-k+1] ) either ok. So. Far (Why? ) (( i k. a[i] = a[n-i+1]) = ok. So. Far) or a[k] a[n-k+1] Is palindrome Either way, So, i n div 2. a[i] = a[n-i+1] if ok. So. Far i. a[i] a[n-i+1] And, ( i n div 2. a[i] = a[n-i+1]) if ok. So. Far CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 8

An Invariant for Every Loop q Software engineer must understand each loop § Loop invariants specify essential properties of loop q Software engineer states invariant for each loop § Invariant encapsulates all important properties § Sketch of proof or informal reasoning confirm correct results § Fools and amateurs can skip this step … Professionals cannot q Advantages of practicing this discipline § Way improves software quality ü Necessary to produce defect-free software § Facilitates software review and maintenance § Saves time, overall CS 1813 Discrete Mathematics, Univ Oklahoma Copyright © 2000 by Rex Page 9

End of Lecture 10