Lecture 17 Review RC circuit natural response RL

Lecture 17 • Review: • RC circuit natural response • RL circuit natural response • General first order system natural response • First order circuit examples • Related educational materials: –Chapter 7. 3

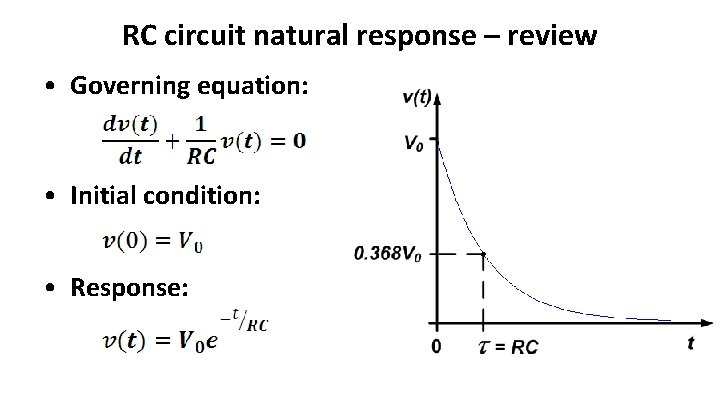
RC circuit natural response – review • Governing equation: • Initial condition: • Response:

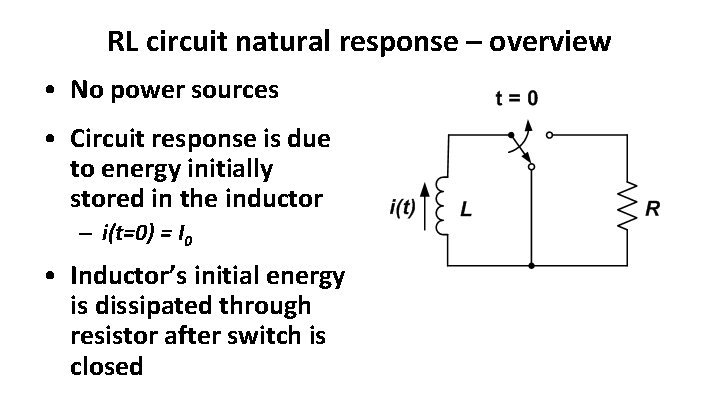
RL circuit natural response – overview • No power sources • Circuit response is due to energy initially stored in the inductor – i(t=0) = I 0 • Inductor’s initial energy is dissipated through resistor after switch is closed

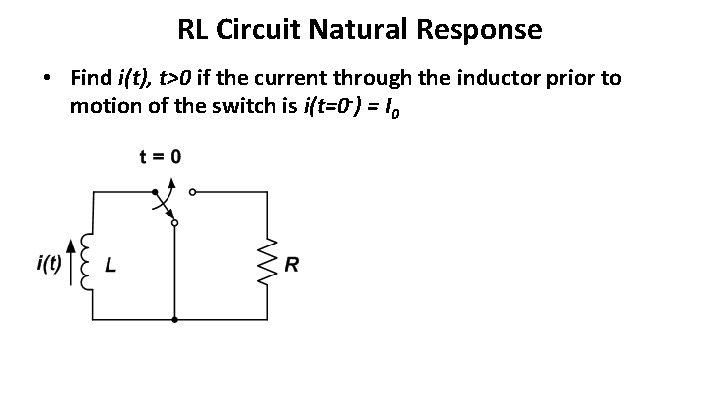
RL Circuit Natural Response • Find i(t), t>0 if the current through the inductor prior to motion of the switch is i(t=0 -) = I 0

• Derive governing first order differential equation on previous slide • Determine initial conditions; emphasize that current through inductor cannot change suddenly

RL Circuit Natural Response – continued

• Finish derivation on previous slide • Sketch response on previous slide

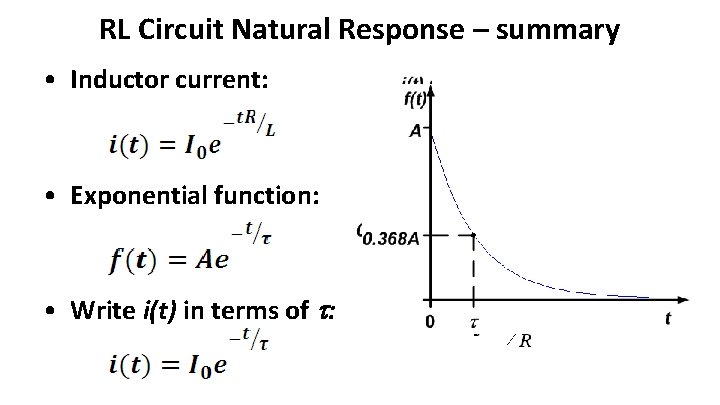
RL Circuit Natural Response – summary • Inductor current: • Exponential function: • Write i(t) in terms of :

• Notes: • L and R set time constant • Increase L => Time constant increases )more energy to dissipate) • Decreasing R => time constant increases (energy dissipates more slowly)

First order system natural response – summary • RC circuit: • RL circuit: • Solution: • Alternate form of governing equation:

General first order system natural response • Governing equation: • Initial condition: • Form of solution:

Checking results • Our analyses are becoming more mathematically complex • Checking your results against expectations about the circuit’s physical behavior is essential! • For first order circuits, it is often possible to determine the circuit response directly from the circuit itself • However, I recommend doing the math and using the circuit physics to double-check the math

1. Checking the time constant • Governing equation: • RC circuit time constant: • RL circuit time constant: • Note: • In the time constant expressions, the resistance is the equivalent resistance seen by the energy storage element • An outcome of Thévenin’s theorem

Example 1 • Find v(t), t>0

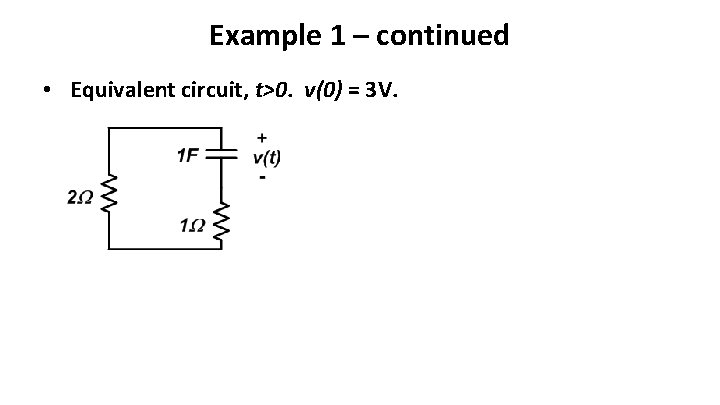
Example 1 – continued • Equivalent circuit, t>0. v(0) = 3 V.

Example 1 – checking results

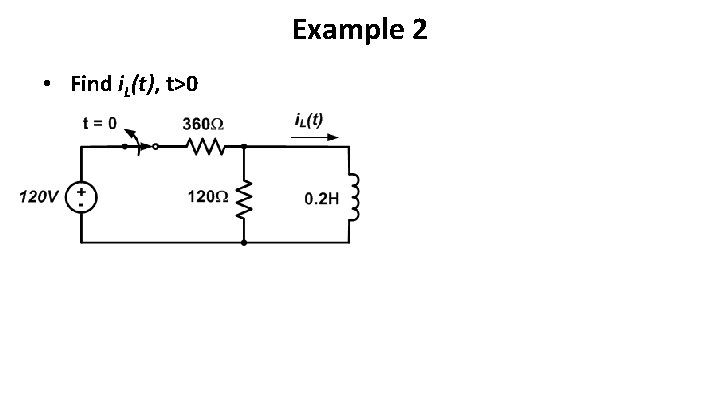
Example 2 • Find i. L(t), t>0

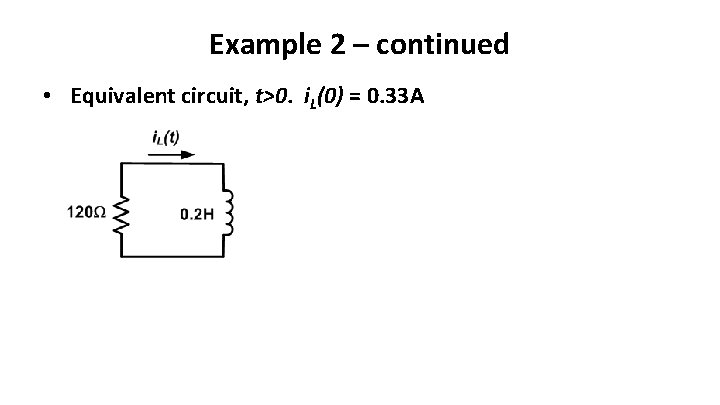
Example 2 – continued • Equivalent circuit, t>0. i. L(0) = 0. 33 A

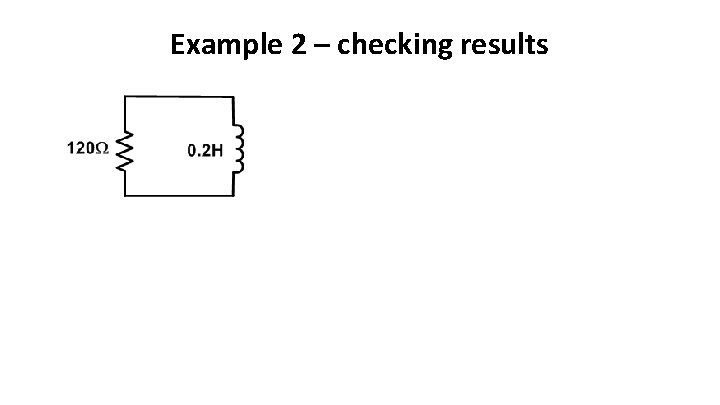
Example 2 – checking results