Lecture 17 Generating Functions Recap Generating functions are

Lecture 17 Generating Functions

Recap Generating functions are defined by a sequence as follows: Thus: For every sequence there a generating function and for every sequence there is a generating function. Idea: Use properties of functions to solve problems about sequences.

Recap: Important Gen. Functions binomial coefficients adding sequences multiplying sequences

Recap: Extended Binomial Coeff. The binomial theorem was extended to real values for u, using the definition of extended binomial coefficients.

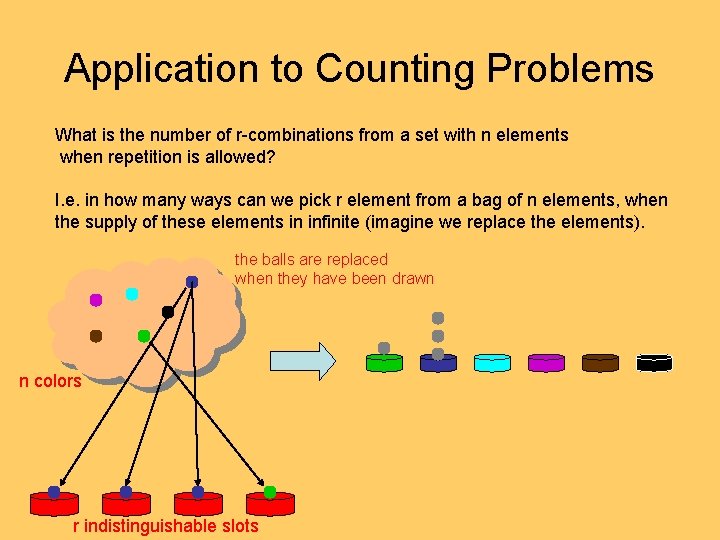
Application to Counting Problems What is the number of r-combinations from a set with n elements when repetition is allowed? I. e. in how many ways can we pick r element from a bag of n elements, when the supply of these elements in infinite (imagine we replace the elements). the balls are replaced when they have been drawn n colors r indistinguishable slots

Application to Counting (1+x+x^2+x^3+x^4+. . . . ) x x^3 1 1 = x^4 This is just one combination of dividing 4 balls into 6 slots. In general we can choose any combination of terms as long as the powers add up to 4. The number of r-combinations of a set with n elements with repetition is therefore equal to the coefficient in front of the term x^4 in the generating function: G(x)=(1+x+x^2+. . . )^n

r-Combinations with repetion Now let’s compute that coefficient: Looks familiar ?

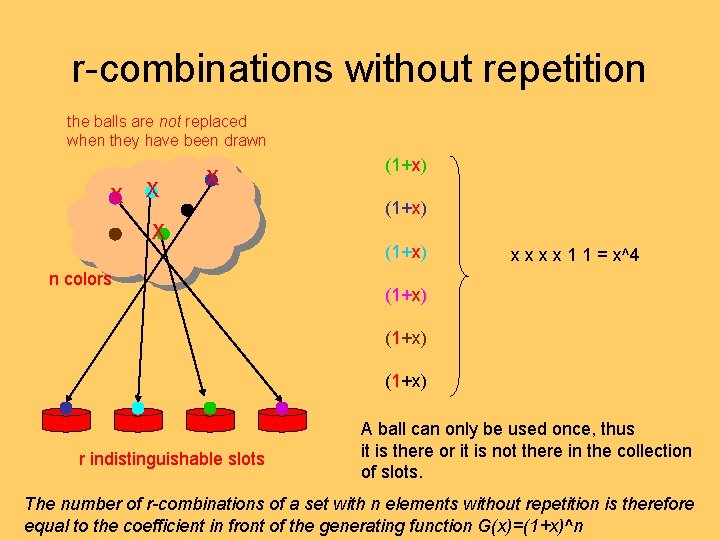
r-combinations without repetition the balls are not replaced when they have been drawn X X n colors (1+x) x x 1 1 = x^4 (1+x) r indistinguishable slots A ball can only be used once, thus it is there or it is not there in the collection of slots. The number of r-combinations of a set with n elements without repetition is therefore equal to the coefficient in front of the generating function G(x)=(1+x)^n

r-combinations without repetition So let’s compute that coefficient: Looks familiar? binomial theorem

Counting with constraints Now let’s say, we want to make sure that we pick r elements out of n with repetition allowed, but we want at least 1 element from each kind: G(x) = (x+x^2+x^3+. . . )^n We are looking for the coefficient of x^r. Here we used the calculation of a few slides back. Here we redefined: j=n+k Note that choosing less than n objects is not possible!

Solving Recurrence Relations therefore we have found that a[k]=2 x 3^k is the solution!

Some Exercises (white board)

6. 5 Inclusion-Exclusion U A A B It’s simply a matter of not over-counting the blue area in the intersection.

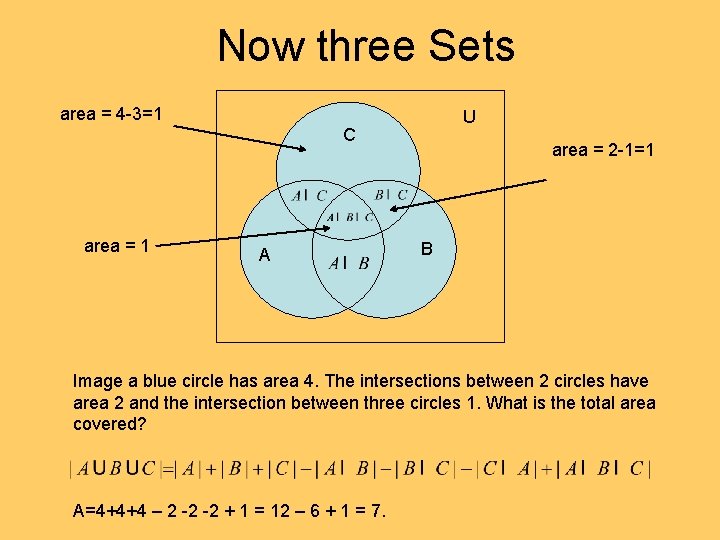
Now three Sets area = 4 -3=1 U C area = 1 A area = 2 -1=1 B Image a blue circle has area 4. The intersections between 2 circles have area 2 and the intersection between three circles 1. What is the total area covered? A=4+4+4 – 2 -2 -2 + 1 = 12 – 6 + 1 = 7.

General Case Proof: We show that each element is counted exactly once. Assume element ‘a’ is in r sets out of the n sets A 1, . . . , An. -The first term counts ‘a’ r-times=C(r, 1). -The second term counts ‘a’ -C(r, 2) times (there are C(r, 2) pairs in a set of r elements). -The k’th term counts ‘a’ -C(r, k) times (there are C(r, k) k-subsets in a set of r elements). -. . . - If k=r then there are precisely (-1)^(r+1) C(r, r) terms. - For k>r ‘a’ is not in the intersection: it is counted 0 times. Total: C(r, 1)-C(r, 2)+. . . +(-1)^(r+1)C(r, r) Now use: to show that each element is counted exactly once.