Lecture 16 LR LC Electromagnetic Waves Looking forward

Lecture 16: LR, LC, Electromagnetic Waves Looking forward at … • LR circuits, LC oscillator • how electromagnetic waves are generated. © 2016 Pearson Education Inc.

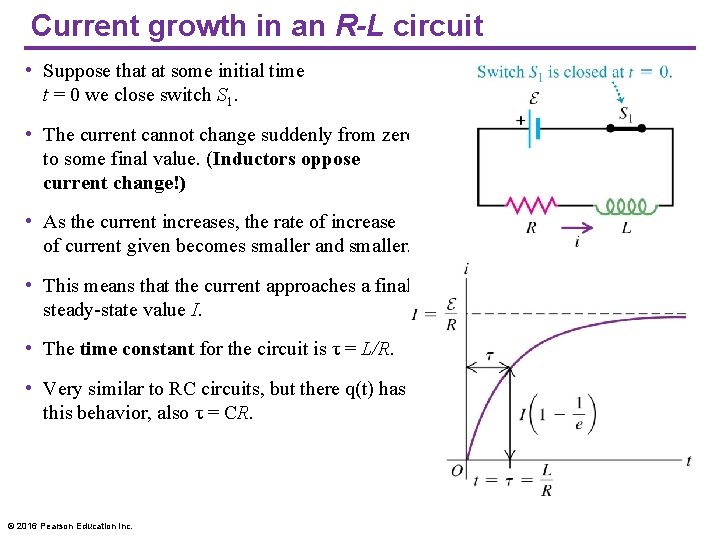
Current growth in an R-L circuit • Suppose that at some initial time t = 0 we close switch S 1. • The current cannot change suddenly from zero to some final value. (Inductors oppose current change!) • As the current increases, the rate of increase of current given becomes smaller and smaller. • This means that the current approaches a final, steady-state value I. • The time constant for the circuit is τ = L/R. • Very similar to RC circuits, but there q(t) has this behavior, also τ = CR. © 2016 Pearson Education Inc.

Bit before that: The L-C circuit oscillation •

The L-C circuit: Oscillation: Step 2 of 4 • © 2016 Pearson Education Inc.

The L-C circuit: Oscillation: Step 3 of 4 • Although the capacitor was completely discharged in step 2, the current persists, and the capacitor begins to charge with polarity opposite to that in the initial state. • Eventually, the current and the magnetic field reach zero, and the capacitor has been charged in the sense opposite to its initial polarity. • Shown is this situation: The capacitor is fully charged, the current is zero, and the circuit’s energy is all stored in the electric field. © 2016 Pearson Education Inc.

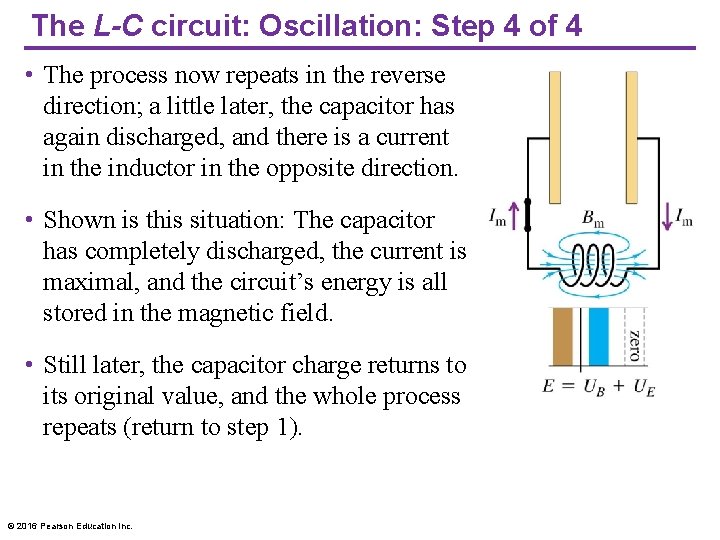
The L-C circuit: Oscillation: Step 4 of 4 • The process now repeats in the reverse direction; a little later, the capacitor has again discharged, and there is a current in the inductor in the opposite direction. • Shown is this situation: The capacitor has completely discharged, the current is maximal, and the circuit’s energy is all stored in the magnetic field. • Still later, the capacitor charge returns to its original value, and the whole process repeats (return to step 1). © 2016 Pearson Education Inc.

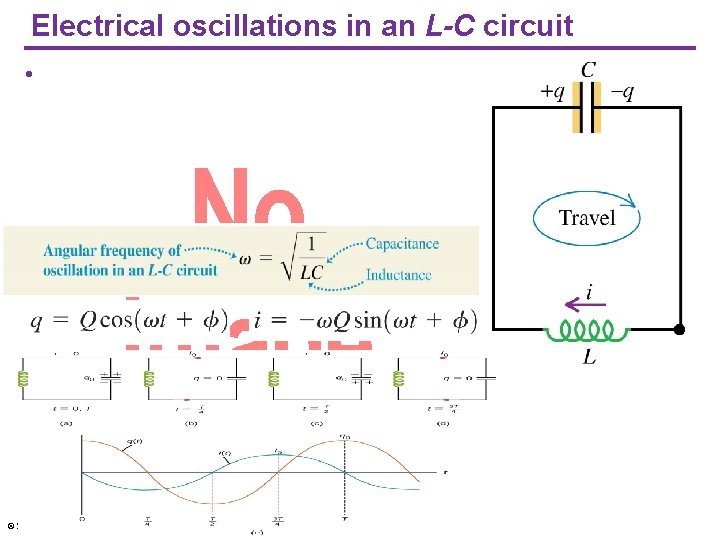
Electrical oscillations in an L-C circuit • © 2016 Pearson Education Inc.

Electrical and mechanical oscillations: analogies © 2016 Pearson Education Inc.

Introduction • Why do metals reflect light? • We will see that light is an electromagnetic wave. • There are many other examples of electromagnetic waves, such as radio waves and x rays. • Unlike sound or waves on a string, these waves do not require a medium to travel. © 2016 Pearson Education Inc.

James Clerk Maxwell and electromagnetic waves • The Scottish physicist James Clerk Maxwell (1831– 1879) was the first person to truly understand the fundamental nature of light. • He proved in 1865 that an electromagnetic disturbance should propagate in free space with a speed equal to that of light. • From this, he deduced correctly that light was an electromagnetic wave. © 2016 Pearson Education Inc.

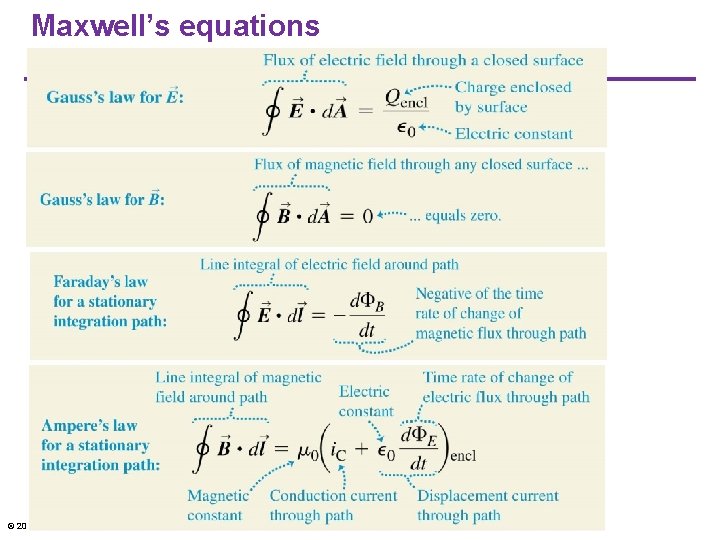
Maxwell’s equations © 2016 Pearson Education Inc.

Electricity, magnetism, and light • According to Maxwell’s equations, an accelerating electric charge or a changing current must produce electromagnetic waves. • For example, power lines carry a strong alternating current generating electromagnetic waves (this means that a substantial amount of charge is accelerating back and forth). • These waves can produce a buzzing sound from your car radio when you drive near the lines. © 2016 Pearson Education Inc.

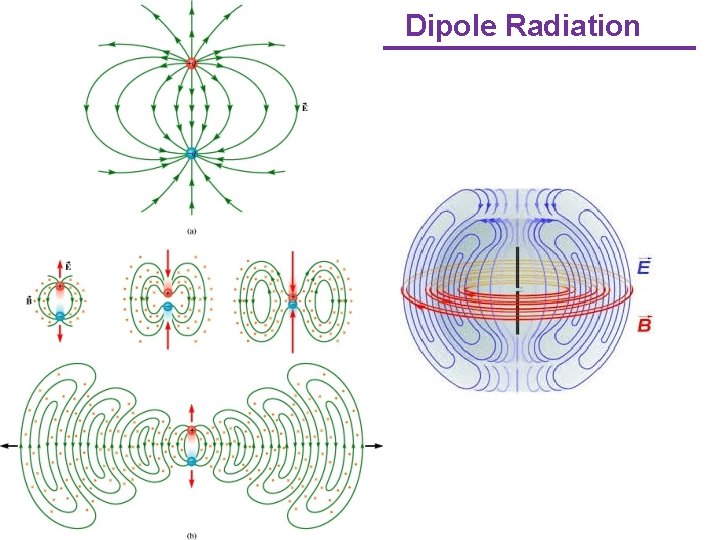
Dipole Radiation

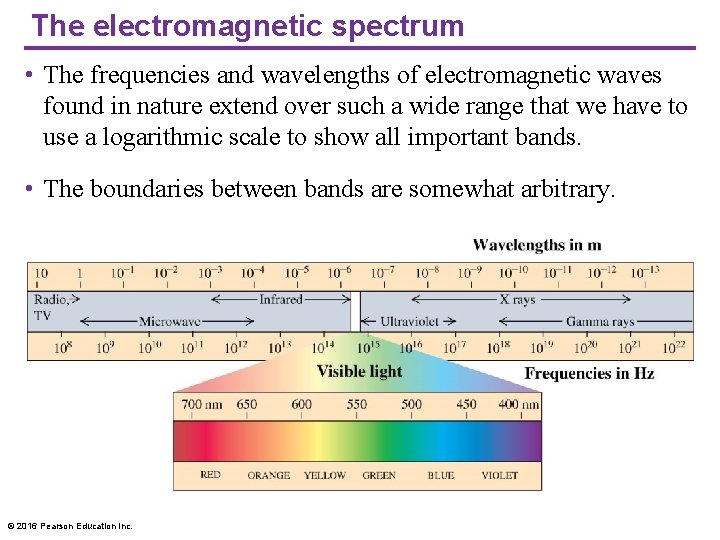
The electromagnetic spectrum • The frequencies and wavelengths of electromagnetic waves found in nature extend over such a wide range that we have to use a logarithmic scale to show all important bands. • The boundaries between bands are somewhat arbitrary. © 2016 Pearson Education Inc.

Visible light • Visible light is the segment of the electromagnetic spectrum that we can see. • Visible light extends from the violet end (400 nm) to the red end (700 nm). © 2016 Pearson Education Inc.

Ultraviolet vision • Many insects and birds can see ultraviolet wavelengths that humans cannot. • As an example, the left-hand photo shows how black-eyed Susans look to us. • The right-hand photo (in false color), taken with an ultraviolet -sensitive camera, shows how these same flowers appear to the bees that pollinate them. • Note the prominent central spot that is invisible to humans. © 2016 Pearson Education Inc.

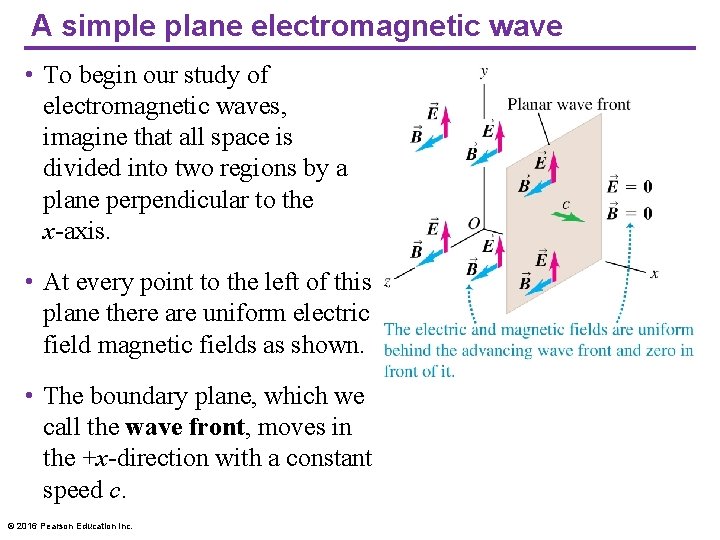
A simple plane electromagnetic wave • To begin our study of electromagnetic waves, imagine that all space is divided into two regions by a plane perpendicular to the x-axis. • At every point to the left of this plane there are uniform electric field magnetic fields as shown. • The boundary plane, which we call the wave front, moves in the +x-direction with a constant speed c. © 2016 Pearson Education Inc.

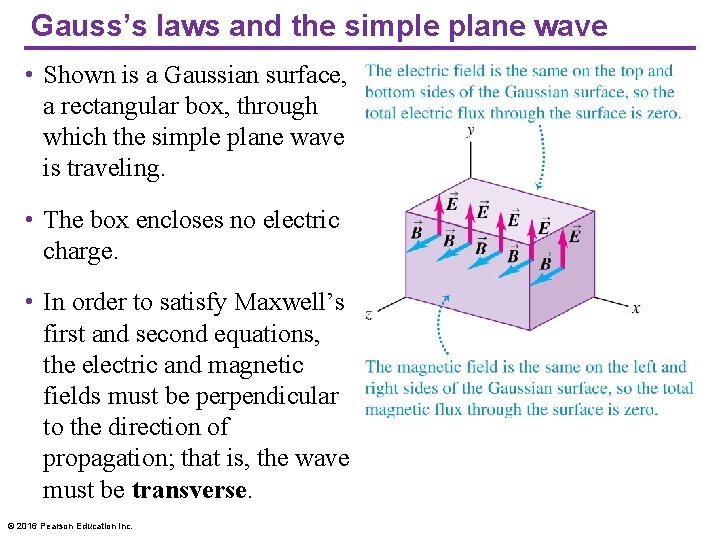
Gauss’s laws and the simple plane wave • Shown is a Gaussian surface, a rectangular box, through which the simple plane wave is traveling. • The box encloses no electric charge. • In order to satisfy Maxwell’s first and second equations, the electric and magnetic fields must be perpendicular to the direction of propagation; that is, the wave must be transverse. © 2016 Pearson Education Inc.