Lecture 15 Tables and OOP 1 Last Lecture

Lecture 15: Tables and OOP 1

Last Lecture: Stack Data Abstraction • Constructor: (make-stack) returns an empty stack • Selector: (top stack) returns current top element from a stack • Mutators and operations: (insert stack elem) returns a new stack with the element added to the top of the stack (delete stack) returns a new stack with the top element removed from the stack (empty-stack? stack) returns #t if no elements, #f otherwise 2

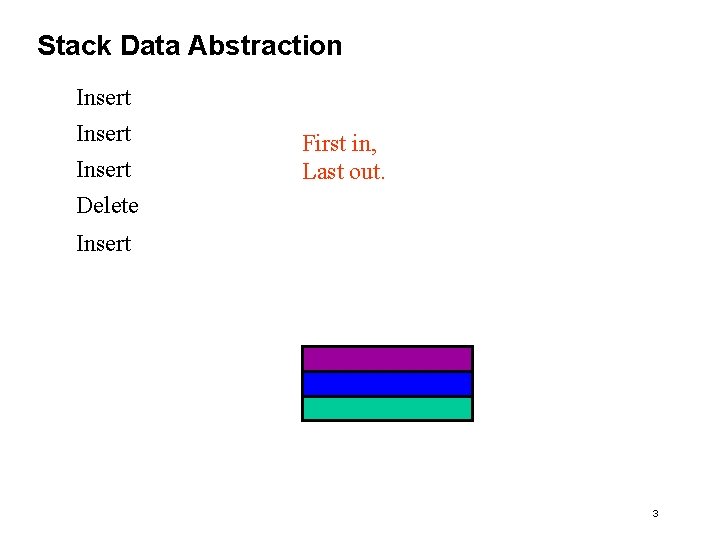
Stack Data Abstraction Insert Delete First in, Last out. Insert 3

Queue Data Abstraction • Constructor: (make-queue) • Selector: (front-queue q) returns an empty queue returns the object at the front of the queue. If queue is empty signals error • Mutators and operations: (insert-queue q elt) returns a new queue with elt at the rear of the queue (delete-queue q) returns a new queue with the item at the (empty-queue? q) front of the queue removed tests if the queue is empty 5

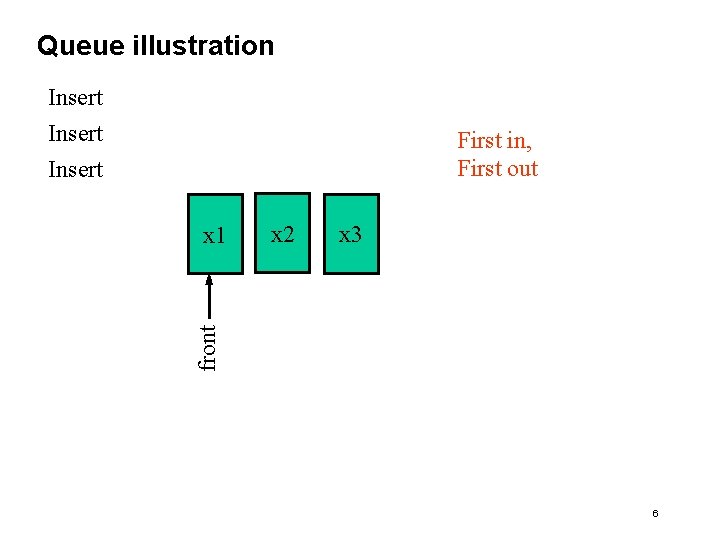
Queue illustration Insert First in, First out Insert x 2 x 3 front x 1 6

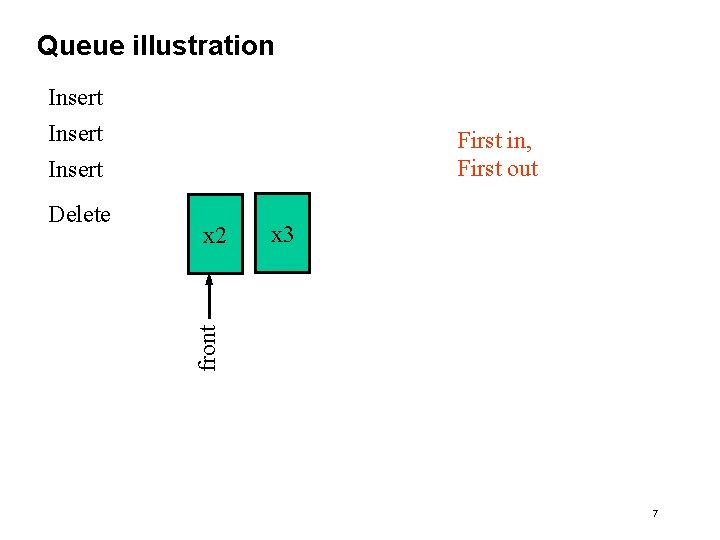
Queue illustration Insert First in, First out Insert x 2 x 3 front Delete 7

Queue Contract • If q is a queue, created by (make-queue) and subsequent queue procedures, where i is the number of insertions, j is the number of deletions, and xi is the ith item inserted into q , then • If j>i then it is an error • If j=i then (empty-queue? q) is true, and (front-queue q) and (delete-queue q) are errors. • If j<i then (front-queue q) = xj+1 8

Today: Tables -- get and put 9

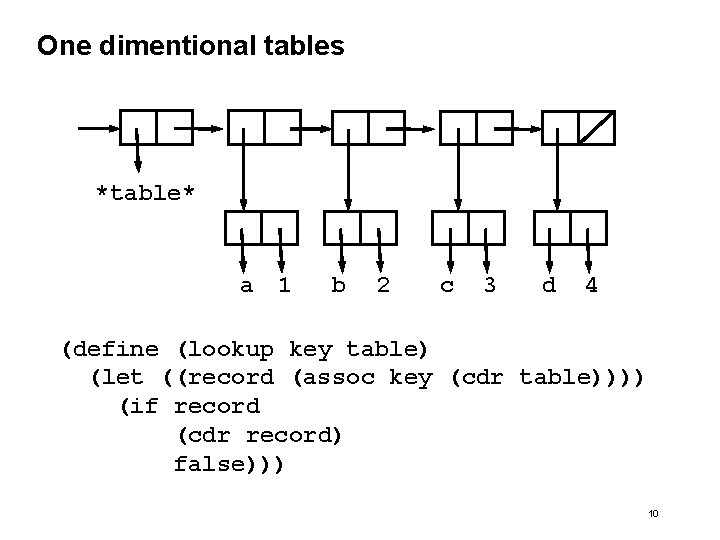
One dimentional tables *table* a 1 b 2 c 3 d 4 (define (lookup key table) (let ((record (assoc key (cdr table)))) (if record (cdr record) false))) 10

One dimentional tables (define (lookup key table) (let ((record (assoc key (cdr table)))) (if record (cdr record) false))) (define (assoc key records) (cond ((null? records) false) ((equal? key (caar records)) (car records)) (else (assoc key (cdr records))))) 11

One dimentional tables (define (insert! key value table) (let ((record (assoc key (cdr table)))) (if record (set-cdr! record value) (set-cdr! table (cons key value) (cdr table))))) 'ok) Example: (insert! ‘e 5 table) 12

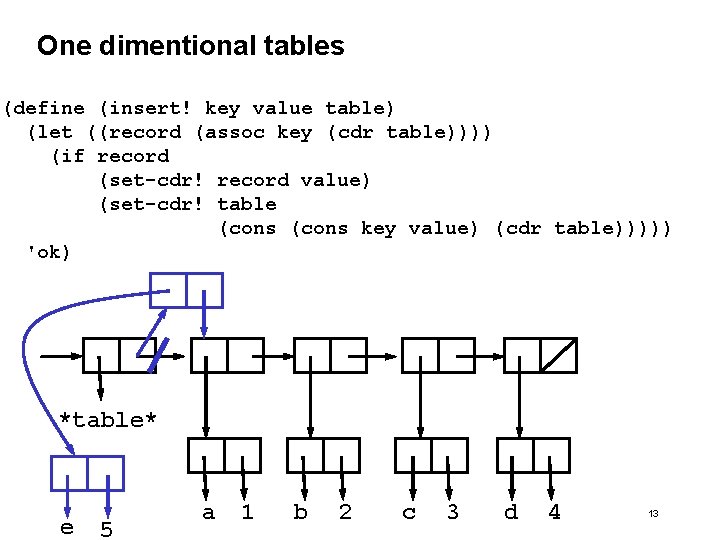
One dimentional tables (define (insert! key value table) (let ((record (assoc key (cdr table)))) (if record (set-cdr! record value) (set-cdr! table (cons key value) (cdr table))))) 'ok) *table* e 5 a 1 b 2 c 3 d 4 13

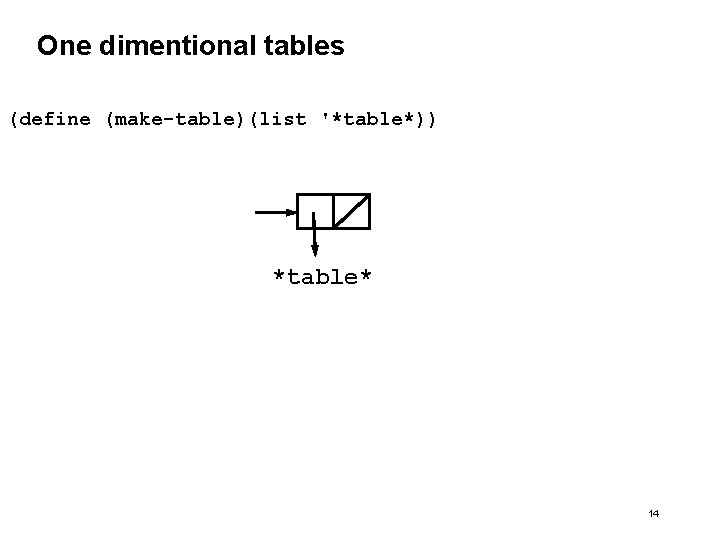
One dimentional tables (define (make-table)(list '*table*)) *table* 14

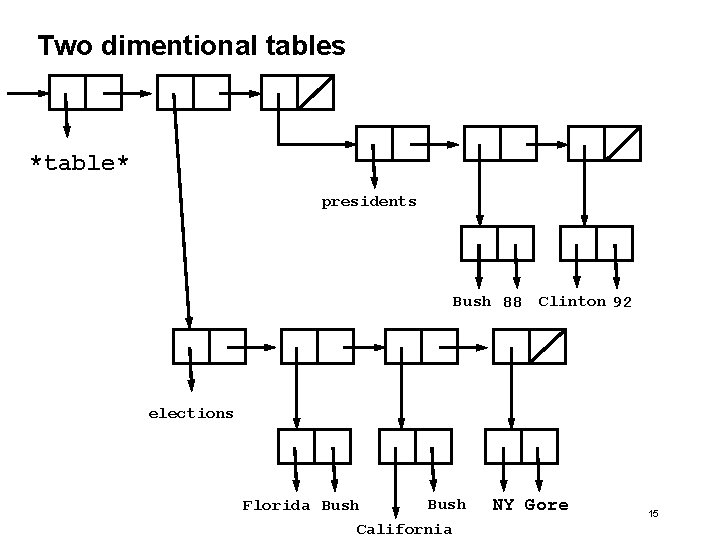
Two dimentional tables *table* presidents Bush 88 Clinton 92 elections Florida Bush California NY Gore 15

Two dimentional tables (define (lookup key-1 key-2 table) (let ((subtable (assoc key-1 (cdr table)))) (if subtable (let ((record (assoc key-2 (cdr subtable)))) (if record (cdr record) false))) Example: (lookup ‘elections ‘Florida table) ==> Bush 16

Two dimentional tables (define (insert! key-1 key-2 value table) (let ((subtable (assoc key-1 (cdr table)))) (if subtable (let ((record (assoc key-2 (cdr subtable)))) (if record (set-cdr! record value) (set-cdr! subtable (cons key-2 value) (cdr subtable))))) (set-cdr! table (cons (list key-1 (cons key-2 value)) (cdr table))))) 'ok) Example: (insert! ‘elections ‘California ‘Gore table) ==> okbb 17

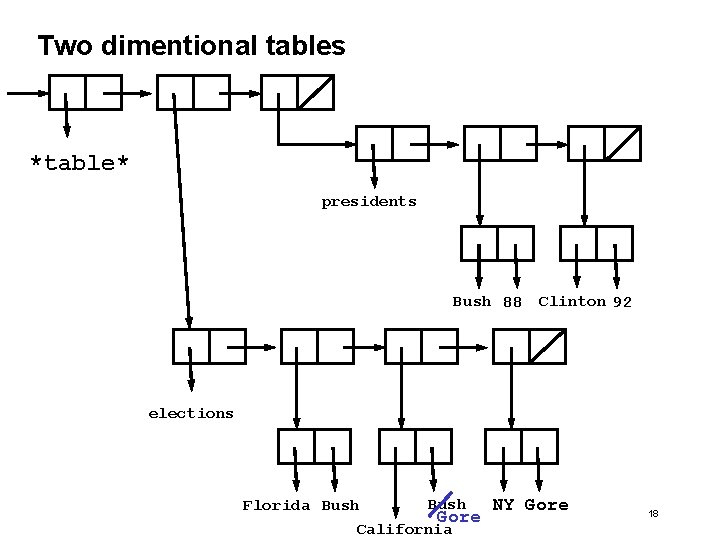
Two dimentional tables *table* presidents Bush 88 Clinton 92 elections Florida Bush Gore California NY Gore 18

Two dimentional tables Example: (insert! ‘singers ‘Madona ‘M table) ==> ok 19

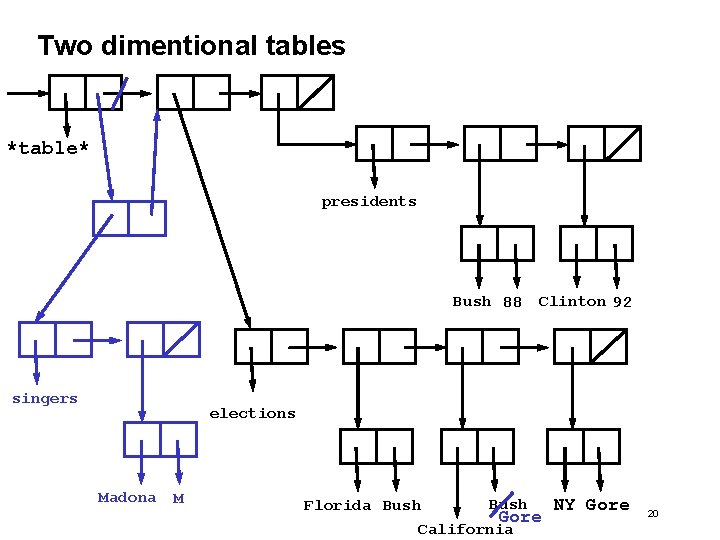
Two dimentional tables *table* presidents Bush 88 singers Clinton 92 elections Madona M Florida Bush Gore California NY Gore 20

Implement get and put (define oper-table (make-table)) (define (put x y v) (insert! x y v oper-table)) (define (get x y) (lookup x y oper-table)) 21

Introduction to Object Oriented Programming 22

One View of Data • Tagged data: • Some complex structure constructed from cons cells • Explicit tags to keep track of data types • Implement a data abstraction as set of procedures that operate on the data • "Generic" operations by looking at types: (define (real-part z) (cond ((rectangular? z) (real-part-rectangular (contents z))) ((polar? z) (real-part-polar (contents z))) (else (error "Unknown type -- REAL-PART" z)))) 23

An Alternative View of Data: Procedures with State • A procedure has • parameters and body as specified by l expression • environment (which can hold name-value bindings!) • Can use procedure to encapsulate (and hide) data, and provide controlled access to that data • constructor, accessors, mutators, predicates, operations • mutation: changes in the private state of the procedure 24

Example: Pair as a Procedure with State (define (cons x (lambda (msg) (cond ((eq? (else y) msg ‘CAR) x) msg ‘CDR) y) msg ‘PAIR? ) #t) (error "pair cannot" msg))))) (define (car p) (p ‘CAR)) (define (cdr p) (p ‘CDR)) (define (pair? p) (and (procedure? p) (p ‘PAIR? ))) 25

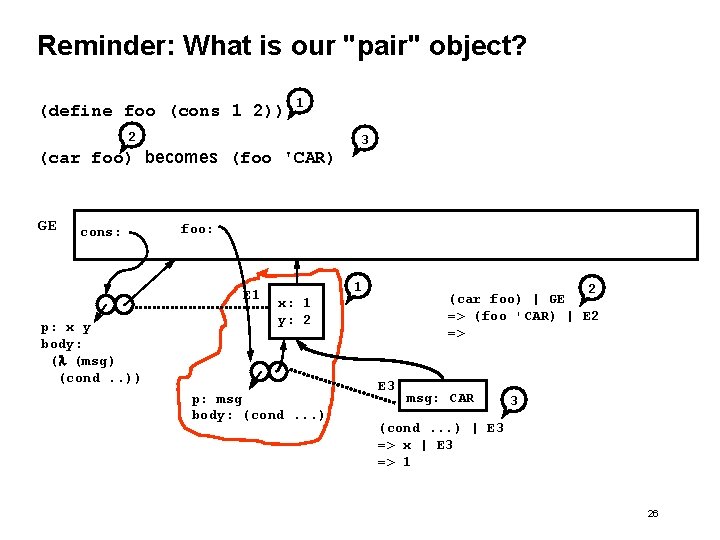
Reminder: What is our "pair" object? (define foo (cons 1 2)) 1 2 (car foo) becomes (foo 'CAR) GE cons: foo: E 1 p: x y body: (l (msg) (cond. . )) 3 1 2 (car foo) | GE => (foo 'CAR) | E 2 => x: 1 y: 2 p: msg body: (cond. . . ) E 3 msg: CAR 3 (cond. . . ) | E 3 => x | E 3 => 1 26

Pair Mutation as Change in State (define (cons x y) (lambda (msg) (cond ((eq? msg ‘CAR) x) ((eq? msg ‘CDR) y) ((eq? msg ‘PAIR? ) #t) ((eq? msg ‘SET-CAR!) (lambda (new-car) (set! x new-car))) ((eq? msg ‘SET-CDR!) (lambda (new-cdr) (set! y new-cdr))) (else (error "pair cannot" msg))))) (define (set-car! p new-car) ((p ‘SET-CAR!) new-car)) (define (set-cdr! p new-cdr) ((p ‘SET-CDR!) new-cdr)) 27

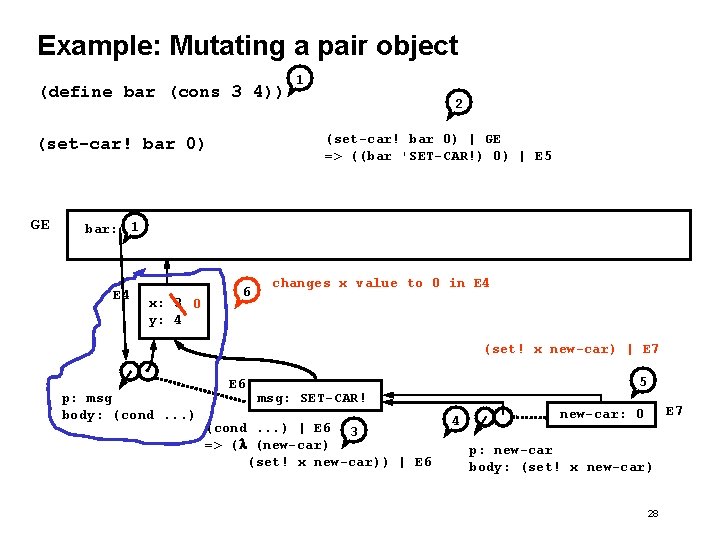
Example: Mutating a pair object (define bar (cons 3 4)) 2 (set-car! bar 0) | GE => ((bar 'SET-CAR!) 0) | E 5 (set-car! bar 0) GE 1 bar: 1 E 4 x: 3 0 y: 4 6 changes x value to 0 in E 4 (set! x new-car) | E 7 p: msg body: (cond. . . ) E 6 5 msg: SET-CAR! (cond. . . ) | E 6 3 => (l (new-car) (set! x new-car)) | E 6 4 E 7 new-car: 0 p: new-car body: (set! x new-car) 28

Message Passing Style - Refinements • lexical scoping for private state and private procedures (define (cons x y) (define (change-car new-car) (set! x new-car)) (define (change-cdr new-cdr) (set! y new-cdr)) (lambda (msg. args) (cond ((eq? msg ‘CAR) x) ((eq? msg ‘CDR) y) ((eq? msg ‘PAIR? ) #t) ((eq? msg ‘SET-CAR!) (change-car (car args))) ((eq? msg ‘SET-CDR!) (change-cdr (car args))) (else (error "pair cannot" msg))))) (define (car p) (define (set-car! p val) (p 'CAR)) (p 'SET-CAR! val)) 29

Message Passing Style - Refinements • lexical scoping for private state and private procedures (define (cons x y) (define (change-car new-car) (set! x new-car)) (define (change-cdr new-cdr) (set! y new-cdr)) (lambda (msg. args) (cond ((eq? msg ‘CAR) x) ((eq? msg ‘CDR) y) ((eq? msg ‘PAIR? ) #t) ((eq? msg ‘SET-CAR!) (change-car (car args))) ((eq? msg ‘SET-CDR!) (change-cdr (car args))) (else (error "pair cannot" msg))))) (define (car p) (define (set-car! p val) (p 'CAR)) (p 'SET-CAR! val)) 31

Programming Styles – Procedural vs. Object-Oriented • Procedural programming: • Organize system around procedures that operate on data (do-something <data> <arg>. . . ) (do-another-thing <data>) • Object-based programming: • Organize system around objects that receive messages (<object> 'do-something <arg>) (<object> 'do-another-thing) • An object encapsulates data and operations • Message passing and procedure are the means to write Object • Oriented code in scheme 32

Tables in OO style (define (make-table) (let ((local-table (list '*table*))) (define (lookup key-1 key-2). . . ) (define (insert! key-1 key-2 value). . . 'ok) (define (dispatch m) (cond ((eq? m 'lookup-proc) lookup) ((eq? m 'insert-proc!) insert!) (else (error "Unknown operation -- TABLE" m)))) dispatch)) 33

Table in OO style (define operation-table (make-table)) (define get (operation-table 'lookup-proc)) (define put (operation-table 'insert-proc!)) 34

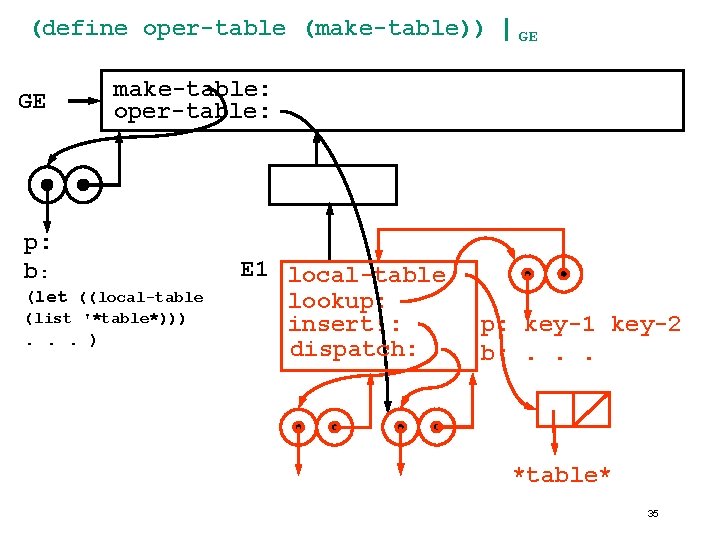
(define oper-table (make-table)) | GE make-table: oper-table: p: b: (let ((local-table (list '*table*))) . . . ) GE E 1 local-table lookup: insert!: dispatch: p: key-1 key-2 b: . . . *table* 35

Object-Oriented Programming Terminology • Class: • specifies the common behavior of entities • in scheme, a "maker" procedure • E. g. cons or make-table in our previous examples • Instance: • A particular object or entity of a given class • in scheme, an instance is a message-handling procedure made by the maker procedure • E. g. foo or bar or oper-table in our previous examples 36

Stacks in OO style (define (make-stack) (let ((top-ptr '())) (define (empty? ) (null? top-ptr)) (define (delete!) (if (null? top-ptr) (error. . . ) (set! top-ptr (cdr top-ptr))) top-ptr ) (define (insert! elmt) (set! top-ptr (cons elmt top-ptr)) top-ptr) (define (top) (if (null? top-ptr) (error. . . ) (car top-ptr))) (define (dispatch op) (cond ((eq? op 'empty? ) ((eq? op 'top) ((eq? op 'insert!) ((eq? op 'delete!))) dispatch)) 37

Stacks in OO style (define s (make-stack)) ==> undef ((s 'insert!) 'a) ==> (a) ((s 'insert!) 'b) ==> (b a) ((s 'top)) ==> b ((s 'delete!)) ==> (a) ((s 'top)) ==> a ((s 'delete!)) ==> () 38

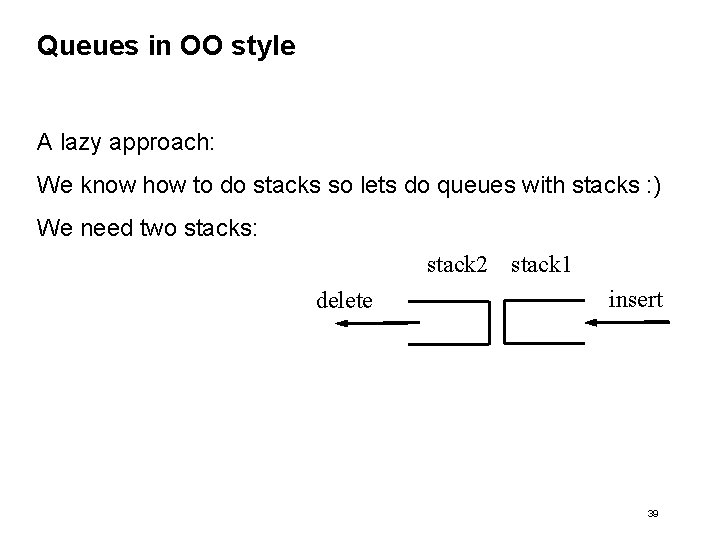
Queues in OO style A lazy approach: We know how to do stacks so lets do queues with stacks : ) We need two stacks: stack 2 stack 1 delete insert 39

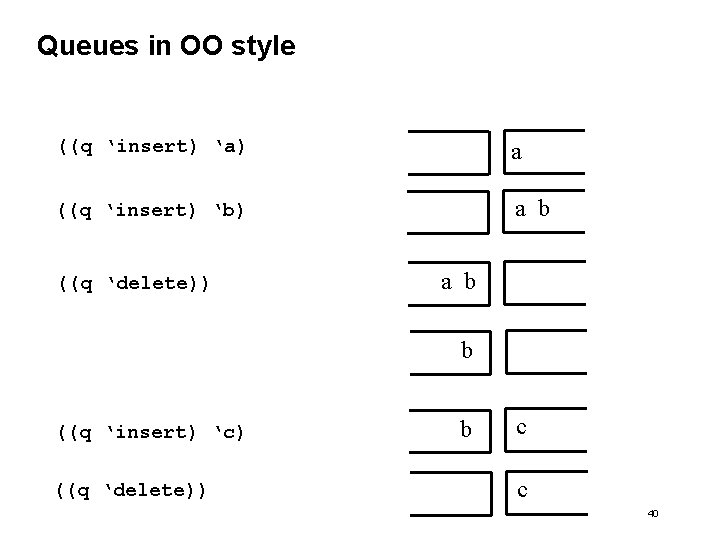
Queues in OO style ((q ‘insert) ‘a) a ((q ‘insert) ‘b) a b ((q ‘delete)) a b b ((q ‘insert) ‘c) ((q ‘delete)) b c c 40

Queues in OO style (define (make-queue) (let ((stack 1 (make-stack)) (stack 2 (make-stack))) (define (reverse-stack s 1 s 2) ________) (define (empty? ) (and ((stack 1 'empty? )) ((stack 2 'empty? )))) (define (delete!) (if ((stack 2 'empty? )) (reverse-stack 1 stack 2)) (if ((stack 2 'empty? )) (error. . . ) ((stack 2 'delete!)))) (define (first) (if ((stack 2 'empty? )) (reverse-stack 1 stack 2)) (if ((stack 2 'empty? )) (error. . . ) ((stack 2 'top)))) (define (dispatch op) (cond ((eq? op 'empty? ) ((eq? op 'first) ((eq? op 'delete!) (else (stack 1 op)))) 41 dispatch))

Queues in OO style Inheritance: One class is a refinement of another The queue class is a subclass of the stack class 42