Lecture 15 n n n Registers Counters Finite

Lecture 15 n n n Registers Counters Finite State Machine (FSM) design 1

Registers n Group of storage elements read/written as a unit ¡ n Collection of flip-flops with common control ¡ n Store related values (e. g. a binary word) Share clock, reset, set lines Example: ¡ ¡ ¡ Storage registers Shift registers Counters 2

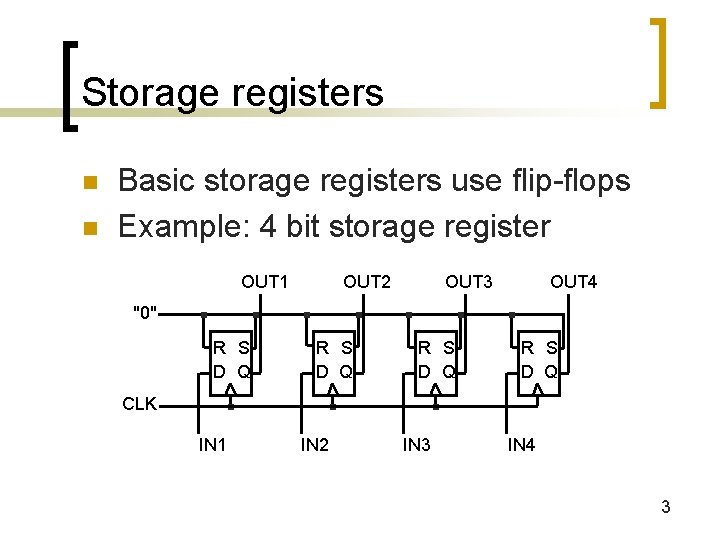
Storage registers n n Basic storage registers use flip-flops Example: 4 bit storage register OUT 1 OUT 2 OUT 3 OUT 4 "0" R S D Q CLK IN 1 IN 2 IN 3 IN 4 3

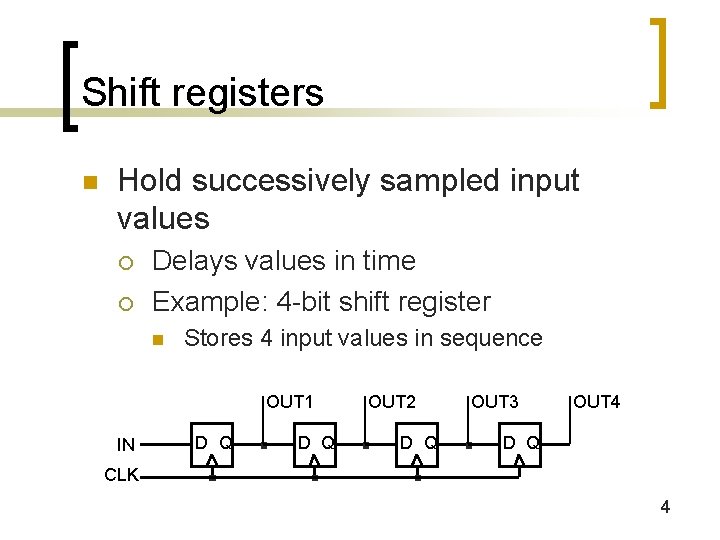
Shift registers n Hold successively sampled input values ¡ ¡ Delays values in time Example: 4 -bit shift register n Stores 4 input values in sequence OUT 1 IN D Q OUT 2 D Q OUT 3 OUT 4 D Q CLK 4

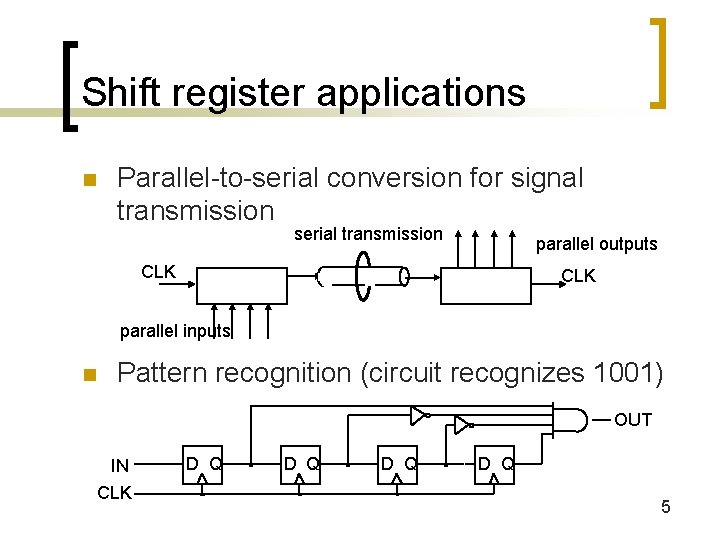
Shift register applications n Parallel-to-serial conversion for signal transmission serial transmission parallel outputs CLK parallel inputs n Pattern recognition (circuit recognizes 1001) OUT IN CLK D Q D Q 5

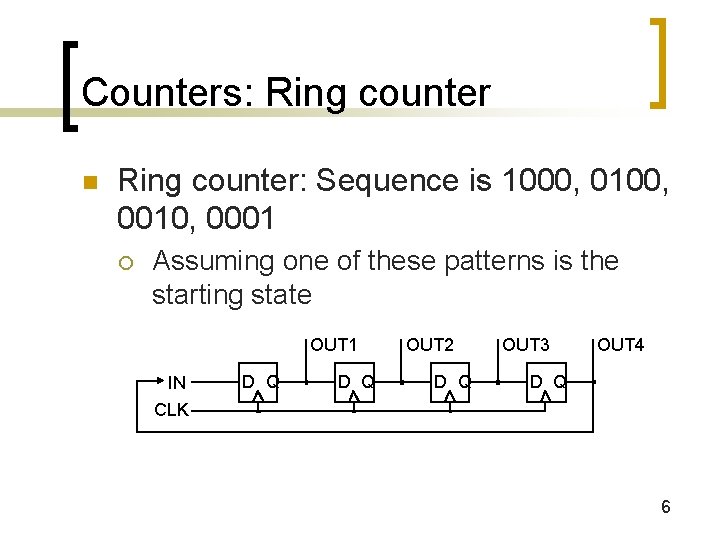
Counters: Ring counter n Ring counter: Sequence is 1000, 0100, 0010, 0001 ¡ Assuming one of these patterns is the starting state OUT 1 IN CLK D Q OUT 2 D Q OUT 3 OUT 4 D Q 6

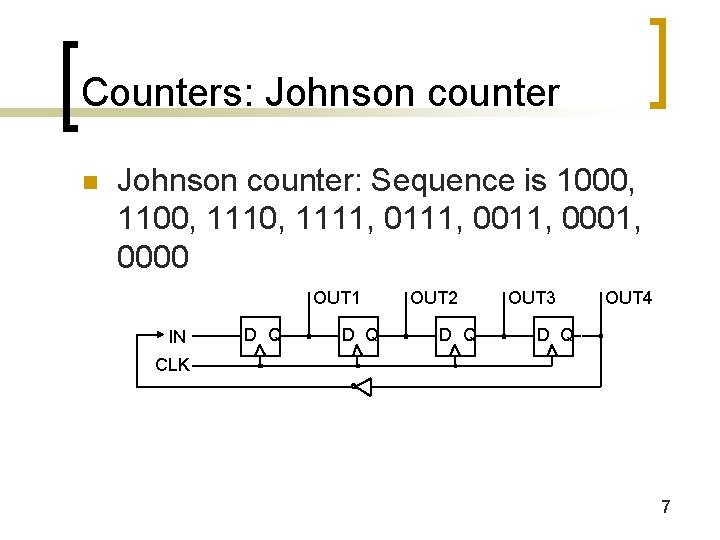
Counters: Johnson counter n Johnson counter: Sequence is 1000, 1110, 1111, 0011, 0000 OUT 1 IN D Q OUT 2 D Q OUT 3 OUT 4 D Q CLK 7

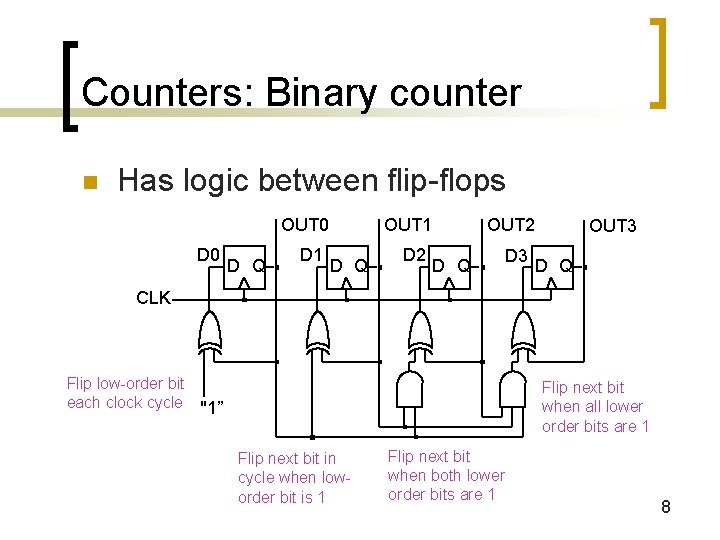
Counters: Binary counter n Has logic between flip-flops OUT 0 D Q D 1 OUT 1 D Q D 2 OUT 2 D Q D 3 OUT 3 D Q CLK Flip low-order bit each clock cycle "1” Flip next bit when all lower order bits are 1 Flip next bit in cycle when loworder bit is 1 Flip next bit when both lower order bits are 1 8

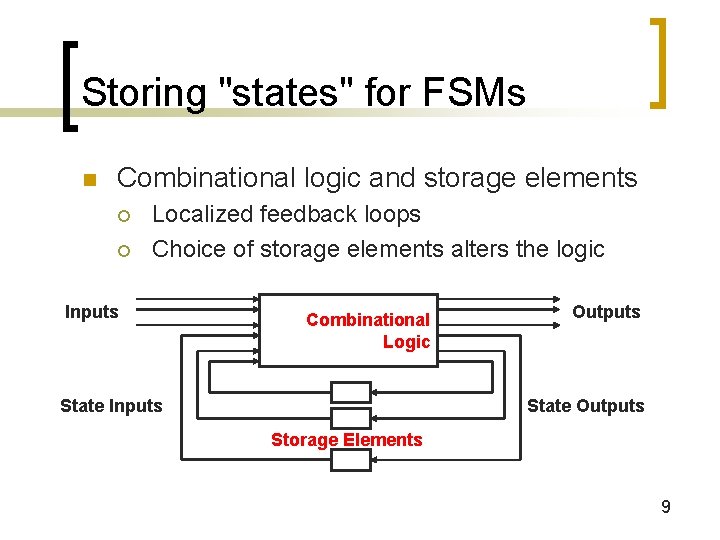
Storing "states" for FSMs n Combinational logic and storage elements ¡ ¡ Localized feedback loops Choice of storage elements alters the logic Inputs Combinational Logic State Inputs Outputs State Outputs Storage Elements 9

Finite-state machines (FSMs) n n States: Possible storage-element values Transitions: Changes in state ¡ n Clock synchronizes the state changes Sequential logic ¡ ¡ Sequences through a series of states Based on inputs and present state 10

FSM design example: Counters 1. 2. 3. Draw a state diagram Draw a state-transition table Encode the next-state functions ¡ 4. Minimize the logic using k-maps Implement the design 11

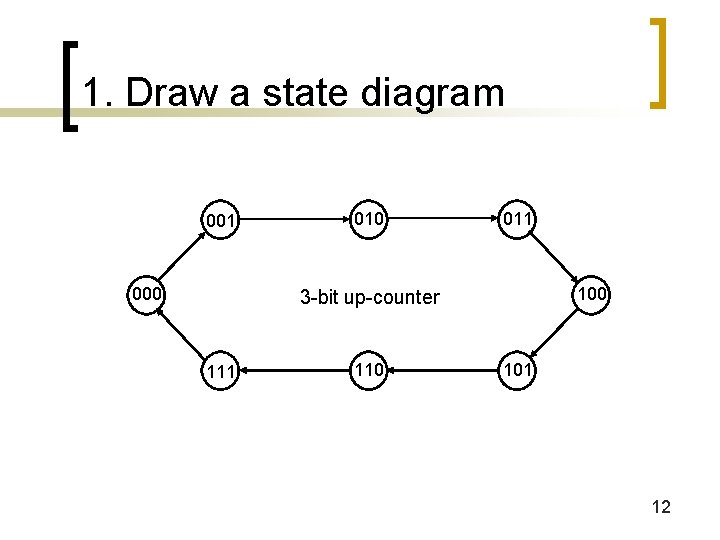
1. Draw a state diagram 001 000 011 100 3 -bit up-counter 111 110 101 12

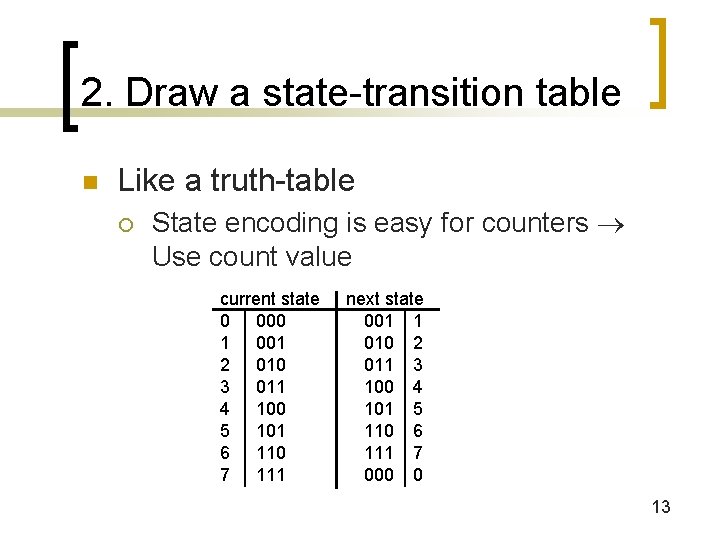
2. Draw a state-transition table n Like a truth-table ¡ State encoding is easy for counters Use count value current state 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 next state 001 1 010 2 011 3 100 4 101 5 110 6 111 7 000 0 13

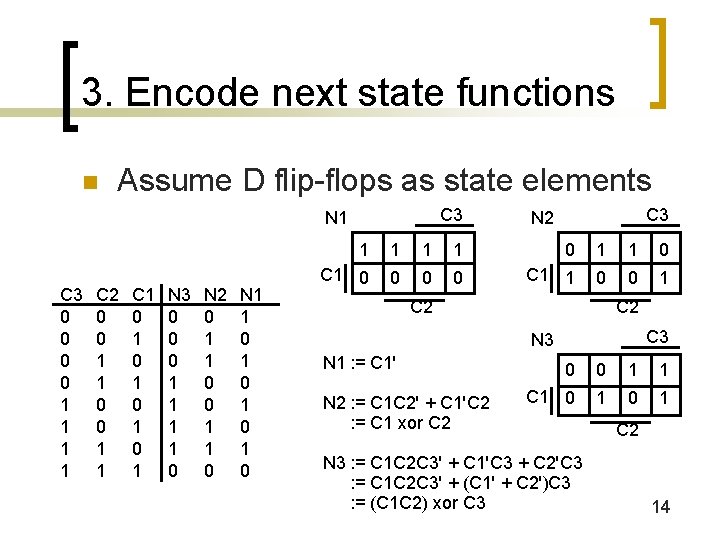
3. Encode next state functions n Assume D flip-flops as state elements C 3 N 1 C 3 0 0 1 1 C 2 0 0 1 1 C 1 0 1 0 1 N 3 0 0 0 1 1 0 N 2 0 1 1 0 N 1 1 0 1 0 C 3 N 2 1 1 0 C 1 0 0 C 1 1 0 0 1 C 2 C 3 N 1 : = C 1' N 2 : = C 1 C 2' + C 1'C 2 : = C 1 xor C 2 0 0 1 1 C 1 0 1 N 3 : = C 1 C 2 C 3' + C 1'C 3 + C 2'C 3 : = C 1 C 2 C 3' + (C 1' + C 2')C 3 : = (C 1 C 2) xor C 3 C 2 14

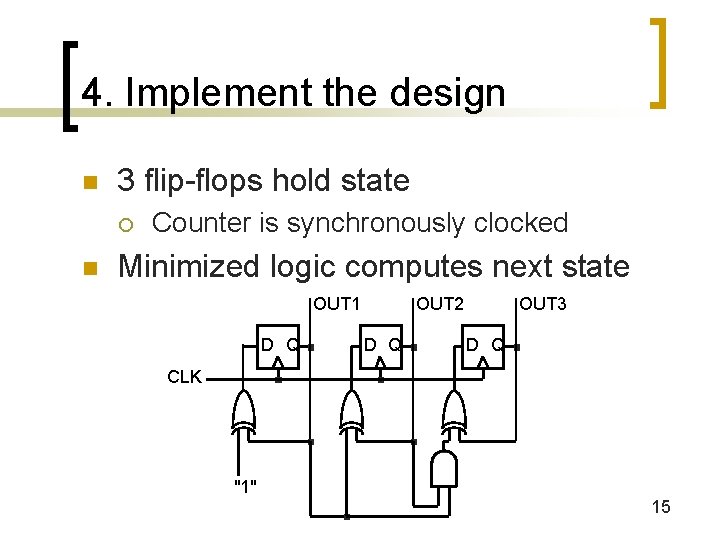
4. Implement the design n 3 flip-flops hold state ¡ n Counter is synchronously clocked Minimized logic computes next state OUT 1 D Q OUT 2 D Q OUT 3 D Q CLK "1" 15

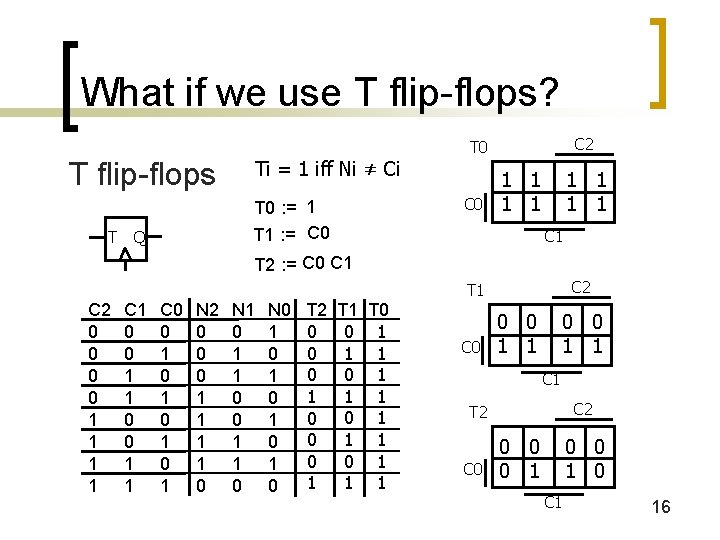
What if we use T flip-flops? T flip-flops T Ti = 1 iff Ni ≠ Ci C 0 T 0 : = 1 T 1 : = C 0 Q C 2 T 0 1 1 1 1 C 1 T 2 : = C 0 C 1 C 2 T 1 C 2 0 0 1 1 C 1 0 0 1 1 C 0 0 1 0 1 N 2 0 0 0 1 1 0 N 1 0 1 1 0 N 0 1 0 1 0 T 2 0 0 0 1 T 1 T 0 0 1 1 1 C 0 0 0 1 1 C 1 C 2 T 2 C 0 0 1 0 C 1 16

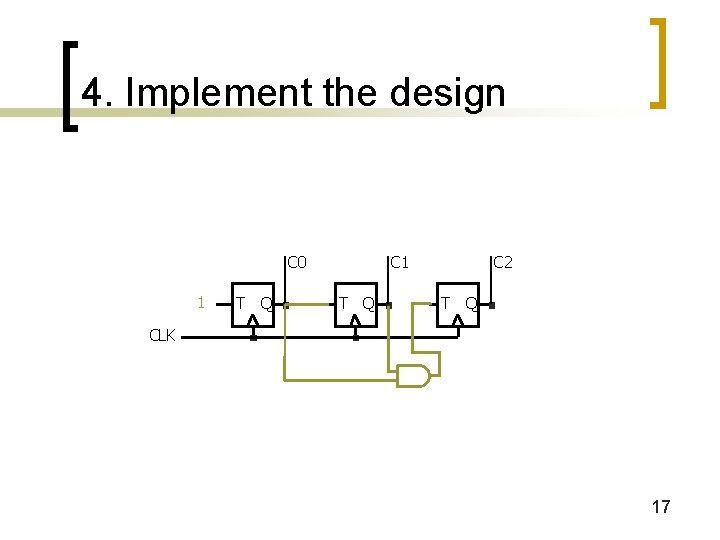
4. Implement the design C 0 1 T Q C 2 T Q CLK 17

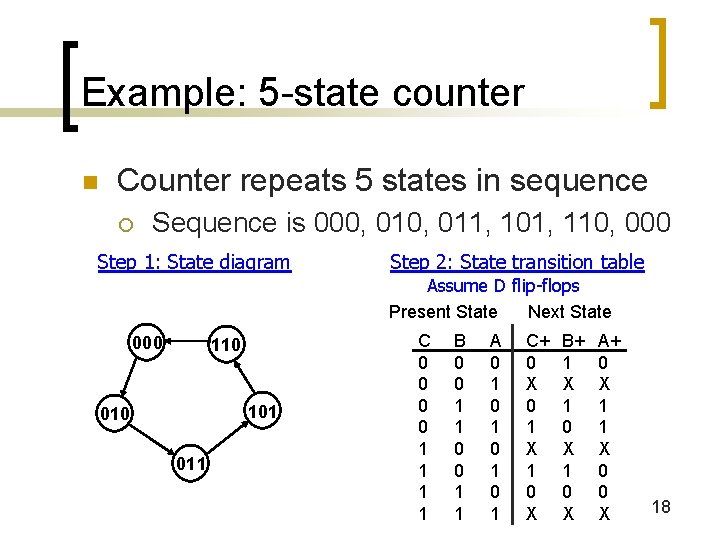
Example: 5 -state counter n Counter repeats 5 states in sequence ¡ Sequence is 000, 011, 101, 110, 000 Step 1: State diagram Step 2: State transition table Assume D flip-flops Present State Next State 000 110 101 010 011 C 0 0 1 1 B 0 0 1 1 A 0 1 0 1 C+ 0 X 0 1 X 1 0 X B+ 1 X 1 0 X A+ 0 X 1 1 X 0 0 X 18

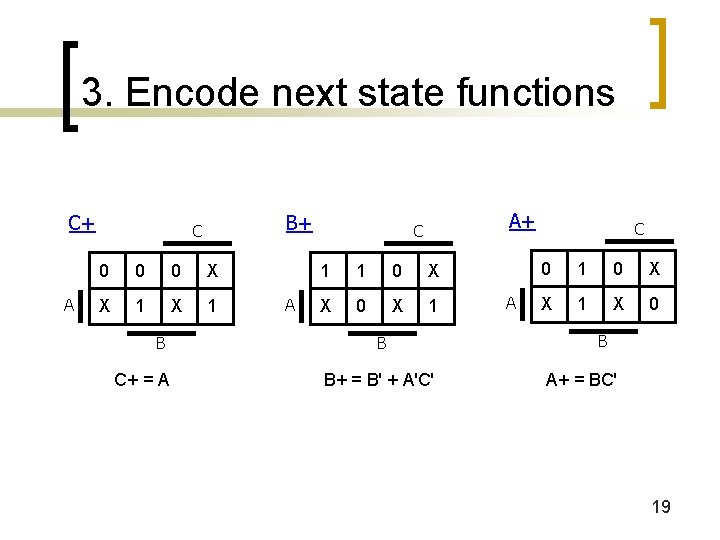
3. Encode next state functions C+ A B+ C 0 0 0 X X 1 B C+ = A A A+ C 1 1 0 X X 0 X 1 B B+ = B' + A'C' A C 0 1 0 X X 1 X 0 B A+ = BC' 19

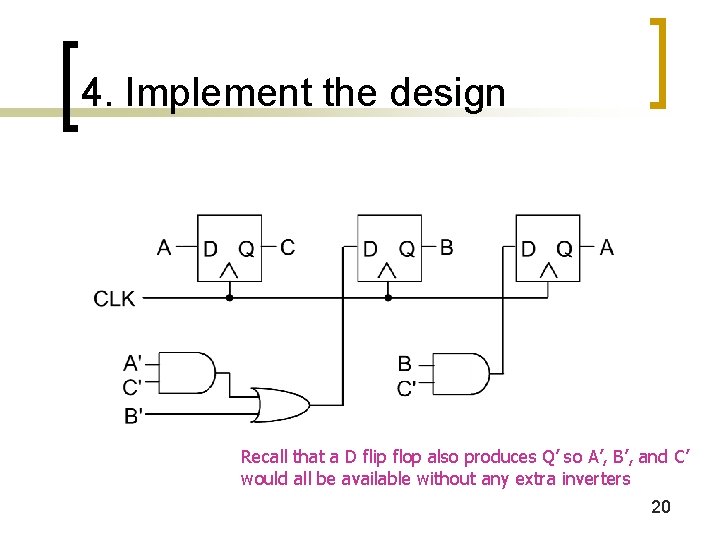
4. Implement the design Recall that a D flip flop also produces Q’ so A’, B’, and C’ would all be available without any extra inverters 20

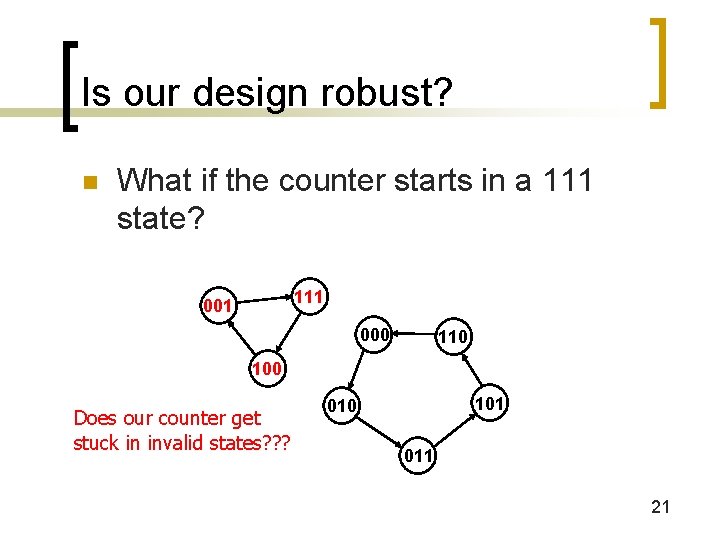
Is our design robust? n What if the counter starts in a 111 state? 111 000 110 100 Does our counter get stuck in invalid states? ? ? 101 010 011 21

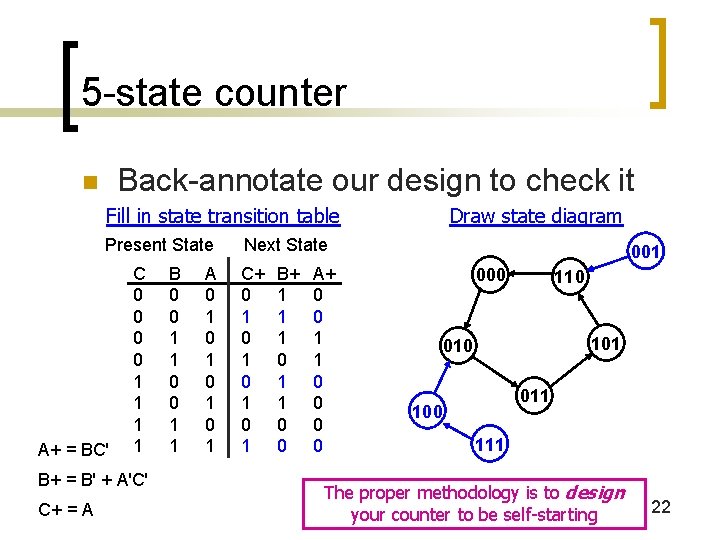
5 -state counter Back-annotate our design to check it n Fill in state transition table Present State A+ = BC' C 0 0 1 1 B+ = B' + A'C' C+ = A B 0 0 1 1 A 0 1 0 1 Draw state diagram Next State C+ 0 1 0 1 B+ 1 1 1 0 0 A+ 0 0 1 1 0 0 001 000 110 101 010 011 100 111 The proper methodology is to design your counter to be self-starting 22

Self-starting counters n Invalid states should always transition to valid states ¡ ¡ n Assures startup Assures bit-error tolerance Design your counters to be self-starting ¡ ¡ ¡ Draw all states in the state diagram Fill in the entire state-transition table May limit your ability to exploit don't cares n Choose startup transitions that minimize the logic 23