Lecture 15 Linear Transformation Eigenvalues and Eigenvectors Last

Lecture 15 Linear Transformation & Eigenvalues and Eigenvectors Last Time - Introduction to Linear Transformations - The Kernel and Range of a Linear Transformation Elementary Linear Algebra R. Larsen et al. (5 Edition) TKUEE翁慶昌-NTUEE SCC_01_2008

Lecture 15: Linear Transformation Today n Matrices for Linear Transformations n Transition Matrix and Similarity n Eigenvalues and Eigenvectors Reading Assignment: Secs 6. 3 -7. 1 Final Exam 2: 20 – 4: 20 Scope: Sections 4. 7 -7. 1 70% Sections 1. 1 – 4. 6 30% Tip: Practice your homework problems and really understand Makeup Lecture n Diagonalization n Symmetric Matrices and Orthogonal Diagonalization n Applications Reading Assignment: Secs 7. 2 -7. 4 15 - 2

What Have You Actually Learned about LT So Far? 15 - 3

Keywords in Section 6. 2: n kernel of a linear transformation T: 線性轉換T的核空間 n range of a linear transformation T: 線性轉換T的值域 n rank of a linear transformation T: 線性轉換T的秩 n nullity of a linear transformation T: 線性轉換T的核次數 n one-to-one: 一對一 n onto: 映成 n isomorphism(one-to-one and onto): 同構 n isomorphic space: 同構的空間 15 - 4

Today n Matrices for Linear Transformations n Transition Matrix and Similarity n Eigenvalues and Eigenvectors 15 - 5

6. 3 Matrices for Linear Transformations n Two representations of the linear transformation T: R 3→R 3 : n Three reasons for matrix representation of a linear transformation: n It is simpler to write. n It is simpler to read. n It is more easily adapted for computer use. 15 - 6

n Thm 6. 10: (Standard matrix for a linear transformation) 15 - 7

Pf: 15 - 8

15 - 9

n Ex 1: (Finding the standard matrix of a linear transformation) Sol: Vector Notation Matrix Notation 15 - 10

n Check: n Note: 15 - 11

n Ex 2: (Finding the standard matrix of a linear transformation) Sol: n Notes: (1) The standard matrix for the zero transformation from Rn into Rm is the m n zero matrix. (2) The standard matrix for the zero transformation from Rn into Rn is the n n identity matrix In 15 - 12

n Composition of T 1: Rn→Rm with T 2: Rm→Rp : n Thm 6. 11: (Composition of linear transformations) 15 - 13

Pf: n Note: 15 - 14

n Ex 3: (The standard matrix of a composition) Sol: 15 - 15

15 - 16

n n Inverse linear transformation: Note: If the transformation T is invertible, then the inverse is unique and denoted by T– 1. 15 - 17

n Ex 6. 12: (Existence of an inverse transformation) (1) T is invertible. (2) T is an isomorphism. (3) A is invertible. n Note: If T is invertible with standard matrix A, then the standard matrix for T– 1 is A– 1. 15 - 18

n Ex 4: (Finding the inverse of a linear transformation) Sol: Show that T is invertible, and find its inverse. 15 - 19

15 - 20

n the matrix of T relative to the bases B and B': Thus, the matrix of T relative to the bases B and B' is 15 - 21

n Transformation matrix for nonstandard bases: 15 - 22

15 - 23

n Ex 5: (Finding a matrix relative to nonstandard bases) Sol: 15 - 24

n Ex 6: Sol: n Check: 15 - 25

n Notes: 15 - 26

Keywords in Section 6. 3: n standard matrix for T: T 的標準矩陣 n composition of linear transformations: 線性轉換的合成 n inverse linear transformation: 反線性轉換 n n matrix of T relative to the bases B and B' : T對應於基底B到 B'的矩陣 matrix of T relative to the basis B: T對應於基底B的矩陣 15 - 27

Today n Matrices for Linear Transformations n Transition Matrix and Similarity n Eigenvalues and Eigenvectors 15 - 28

6. 4 Transition Matrices and Similarity 15 - 29

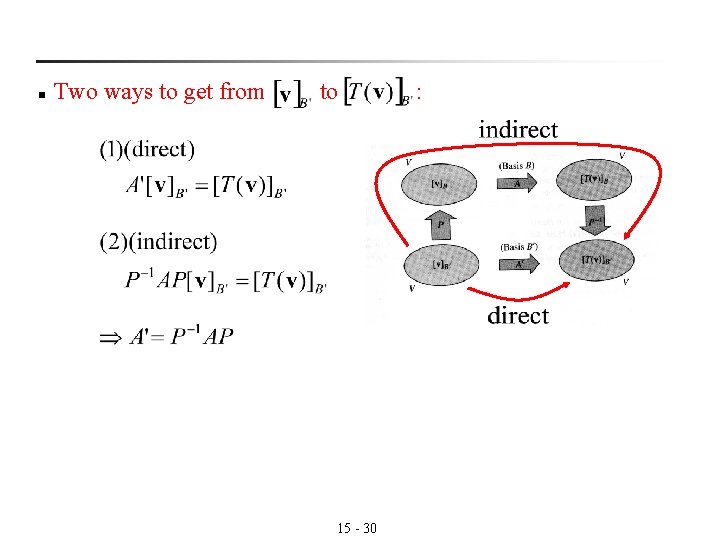
n Two ways to get from to 15 - 30 :

n Ex 1: (Finding a matrix for a linear transformation) Sol: 15 - 31

15 - 32

n Ex 2: (Finding a matrix for a linear transformation) Sol: 15 - 33

n Ex 3: (Finding a matrix for a linear transformation) Sol: 15 - 34

n n Similar matrix: For square matrices A and A‘ of order n, A‘ is said to be similar to A if there exist an invertible matrix P s. t. Thm 6. 13: (Properties of similar matrices) Let A, B, and C be square matrices of order n. Then the following properties are true. (1) A is similar to A. (2) If A is similar to B, then B is similar to A. (3) If A is similar to B and B is similar to C, then A is similar to C. Pf: 15 - 35

n Ex 4: (Similar matrices) 15 - 36

n Ex 5: (A comparison of two matrices for a linear transformation) Sol: 15 - 37

15 - 38

n Notes: Computational advantages of diagonal matrices: 15 - 39

Today n Matrices for Linear Transformations n Transition Matrix and Similarity n Eigenvalues and Eigenvectors 15 - 40

Chapter 7 Eigenvalues and Eigenvectors 7. 1 Eigenvalues and Eigenvectors 7. 2 Diagonalization 7. 3 Symmetric Matrices and Orthogonal Diagonalization Elementary Linear Algebra R. Larsen et al. (5 Edition) TKUEE翁慶昌-NTUEE SCC_01_2008 15 - 41

7. 1 Eigenvalues and Eigenvectors n Eigenvalue problem: If A is an n n matrix, do there exist nonzero vectors x in Rn such that Ax is a scalar multiple of x？ n Eigenvalue and eigenvector: A：an n n matrix ：a scalar x： a nonzero vector in Rn Eigenvalue Eigenvector 15 - 42 n Geometrical Interpretation

n Ex 1: (Verifying eigenvalues and eigenvectors) Eigenvalue Eigenvector 15 - 43

n Thm 7. 1: (The eigenspace of A corresponding to ) If A is an n n matrix with an eigenvalue , then the set of all eigenvectors of together with the zero vector is a subspace of Rn. This subspace is called the eigenspace of . Pf: x 1 and x 2 are eigenvectors corresponding to 15 - 44

n Ex 3: (An example of eigenspaces in the plane) Find the eigenvalues and corresponding eigenspaces of Sol: If For a vector on the x-axis Eigenvalue 15 - 45

For a vector on the y-axis Eigenvalue Geometrically, multiplying a vector (x, y) in R 2 by the matrix A corresponds to a reflection in the y-axis. The eigenspace corresponding to is the x-axis. The eigenspace corresponding to is the y-axis. 15 - 46

n Thm 7. 2: (Finding eigenvalues and eigenvectors of a matrix A Mn n ) Let A is an n n matrix. (1) An eigenvalue of A is a scalar such that . (2) The eigenvectors of A corresponding to are the nonzero n Note: If solutions of . (homogeneous system) has nonzero solutions iff n Characteristic polynomial of A Mn n: n Characteristic equation of A: 15 - 47 .

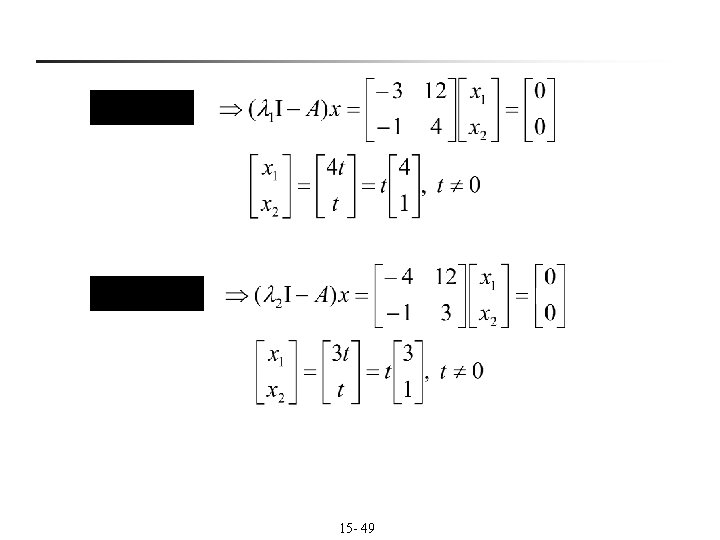
n Ex 4: (Finding eigenvalues and eigenvectors) Sol: Characteristic equation: Eigenvalue: 15 - 48

15 - 49

n Ex 5: (Finding eigenvalues and eigenvectors) Find the eigenvalues and corresponding eigenvectors for the matrix A. What is the dimension of the eigenspace of each eigenvalue? Sol: Characteristic equation: Eigenvalue: 15 - 50

The eigenspace of A corresponding to Thus, the dimension of its eigenspace is 2. 15 - 51 :

n Notes: (1) If an eigenvalue 1 occurs as a multiple root (k times) for the characteristic polynominal, then 1 has multiplicity k. (2) The multiplicity of an eigenvalue is greater than or equal to the dimension of its eigenspace. 15 - 52

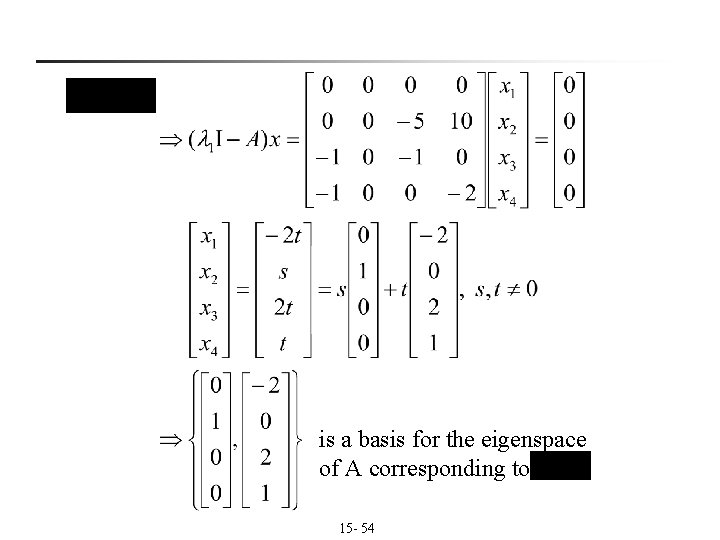
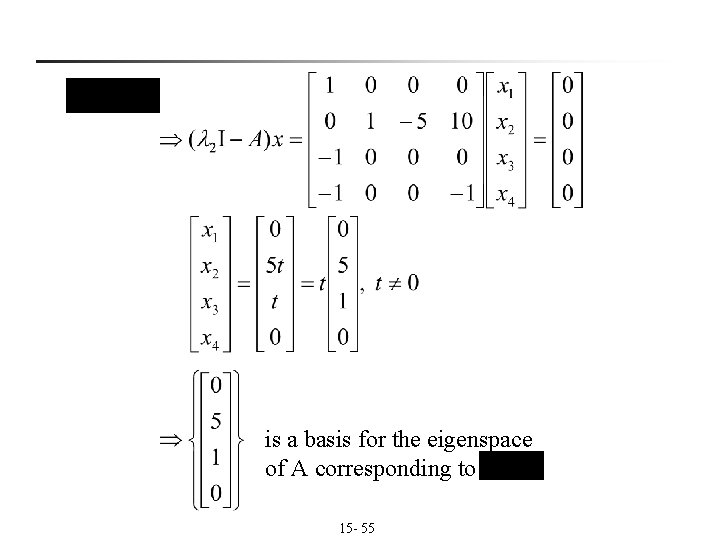
n Ex 6：Find the eigenvalues of the matrix A and find a basis for each of the corresponding eigenspaces. Sol: Characteristic equation: Eigenvalue: 15 - 53

is a basis for the eigenspace of A corresponding to 15 - 54

is a basis for the eigenspace of A corresponding to 15 - 55

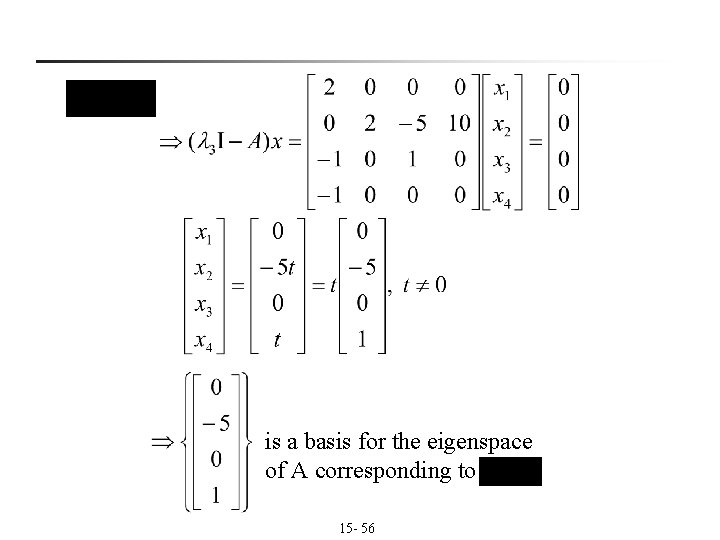
is a basis for the eigenspace of A corresponding to 15 - 56

n n Thm 7. 3: (Eigenvalues for triangular matrices) If A is an n n triangular matrix, then its eigenvalues are the entries on its main diagonal. Ex 7: (Finding eigenvalues for diagonal and triangular matrices) Sol: 15 - 57

n Eigenvalues and eigenvectors of linear transformations: 15 - 58

n Ex 8: (Finding eigenvalues and eigenspaces) Sol: 15 - 59

n Notes: 15 - 60

Keywords in Section 7. 1: n eigenvalue problem: 特徵值問題 n eigenvalue: 特徵值 n eigenvector: 特徵向量 n characteristic polynomial: 特徵多項式 n characteristic equation: 特徵方程式 n eigenspace: 特徵空間 n multiplicity: 重數 15 - 61

Lecture 15: Linear Transformation Today n Matrices for Linear Transformations n Transition Matrix and Similarity n Eigenvalues and Eigenvectors Reading Assignment: Secs 6. 3 -7. 1 Final Exam 2: 20 – 4: 20 Scope: Sections 4. 7 -7. 1: 70%, Sections 1. 1 – 4. 6: 30% Tip: Practice your homework problems and really understand Makeup Lecture n Diagonalization n Symmetric Matrices and Orthogonal Diagonalization n Applications Reading Assignment: Secs 7. 2 -7. 4 15 - 62