Lecture 14 Linear Transformation Last Time Mathematical Models

Lecture 14 Linear Transformation Last Time - Mathematical Models and Least Square Analysis - Inner Product Space Applications - Introduction to Linear Transformations Elementary Linear Algebra R. Larsen et al. (5 Edition) TKUEE翁慶昌-NTUEE SCC_01_2008

Lecture 14: Linear Transformation Today n The Kernel and Range of a Linear Transformation n Matrices for Linear Transformations n Transition Matrix and Similarity Reading Assignment: Secs 6. 2 -6. 4 Next Time n Applications of Linear Transformations n Eigenvalues and Eigenvectors n Diagonalization Reading Assignment: Secs 6. 5 -7. 2 14 - 2

What Have You Actually Learned about LSPs So Far? 14 - 3

Keywords in Section 6. 1: n function: 函數 n domain: 論域 n codomain: 對應論域 n image of v under T: 在T映射下v的像 n range of T: T的值域 n preimage of w: w的反像 n linear transformation: 線性轉換 n linear operator: 線性運算子 n zero transformation: 零轉換 n identity transformation: 相等轉換 14 - 4

Today n The Kernel and Range of a Linear Transformation n Matrices for Linear Transformations n Transition Matrix and Similarity 14 - 5

6. 2 The Kernel and Range of a Linear Transformation n Kernel of a linear transformation T: Let be a linear transformation Then the set of all vectors v in V that satisfy called the kernel of T and is denoted by ker(T). n Ex 1: (Finding the kernel of a linear transformation) Sol: 14 - 6 is

n Ex 2: (The kernel of the zero and identity transformations) (a) T(v)=0 (the zero transformation (b) T(v)=v (the identity transformation n ) ) Ex 3: (Finding the kernel of a linear transformation) Sol: 14 - 7

n Ex 5: (Finding the kernel of a linear transformation) Sol: 14 - 8

14 - 9

n Thm 6. 3: (The kernel is a subspace of V) The kernel of a linear transformation is a subspace of the domain V. Pf: n Note: The kernel of T is sometimes called the nullspace of T. 14 - 10

n Ex 6: (Finding a basis for the kernel) Find a basis for ker(T) as a subspace of R 5. 14 - 11

Sol: 14 - 12

n Corollary to Thm 6. 3: n Range of a linear transformation T: 14 - 13

n Thm 6. 4: (The range of T is a subspace of W) Pf: 14 - 14

n Notes: n Corollary to Thm 6. 4: 14 - 15

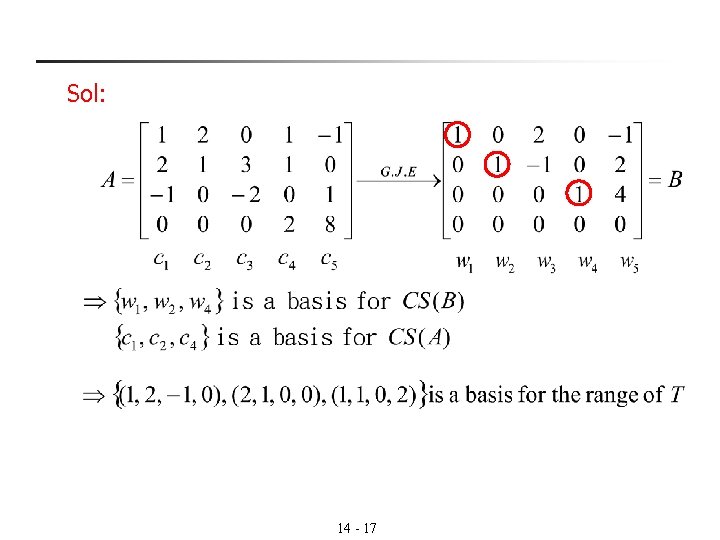
n Ex 7: (Finding a basis for the range of a linear transformation) Find a basis for the range of T. 14 - 16

Sol: 14 - 17

n Rank of a linear transformation T: V→W: n Nullity of a linear transformation T: V→W: n Note: 14 - 18

n Thm 6. 5: (Sum of rank and nullity) Pf: 14 - 19

n Ex 8: (Finding the rank and nullity of a linear transformation) Sol: 6 - 20

n Ex 9: (Finding the rank and nullity of a linear transformation) Sol: 14 - 21

n One-to-one: one-to-one not one-to-one 14 - 22

n Onto: (T is onto W when W is equal to the range of T. ) 14 - 23

n Thm 6. 6: (One-to-one linear transformation) Pf: 14 - 24

n Ex 10: (One-to-one and not one-to-one linear transformation) 14 - 25

n Thm 6. 7: (Onto linear transformation) n Thm 6. 8: (One-to-one and onto linear transformation) Pf: 14 - 26

n Ex 11: Sol: T: Rn→Rm dim(domain of T) (a)T: R 3→R 3 3 3 (b)T: R 2→R 3 2 (c)T: R 3→R 2 (d)T: R 3→R 3 rank(T) nullity(T) 1 -1 onto 0 Yes 2 0 Yes No 3 2 1 No Yes 3 2 1 No No 14 - 27

n n Isomorphism: Thm 6. 9: (Isomorphic spaces and dimension) Two finite-dimensional vector space V and W are Pf: isomorphic if and only if they are of the same dimension. 14 - 28

It can be shown that this L. T. is both 1 -1 and onto. Thus V and W are isomorphic. 14 - 29

n Ex 12: (Isomorphic vector spaces) The following vector spaces are isomorphic to each other. 14 - 30

Keywords in Section 6. 2: n kernel of a linear transformation T: 線性轉換T的核空間 n range of a linear transformation T: 線性轉換T的值域 n rank of a linear transformation T: 線性轉換T的秩 n nullity of a linear transformation T: 線性轉換T的核次數 n one-to-one: 一對一 n onto: 映成 n isomorphism(one-to-one and onto): 同構 n isomorphic space: 同構的空間 14 - 32