Lecture 14 Graph Theory I Discrete Mathematical Structures

Lecture 14: Graph Theory I Discrete Mathematical Structures: Theory and Applications

Learning Objectives 10 q Learn the basic properties of graph theory q Learn about walks, trails, paths, circuits, and cycles in a graph q Explore how graphs are represented in computer memory q Learn about Euler and Hamilton circuits q Learn about isomorphism of graphs q Explore various graph algorithms q Examine planar graphs and graph coloring Discrete Mathematical Structures: Theory and Applications 2

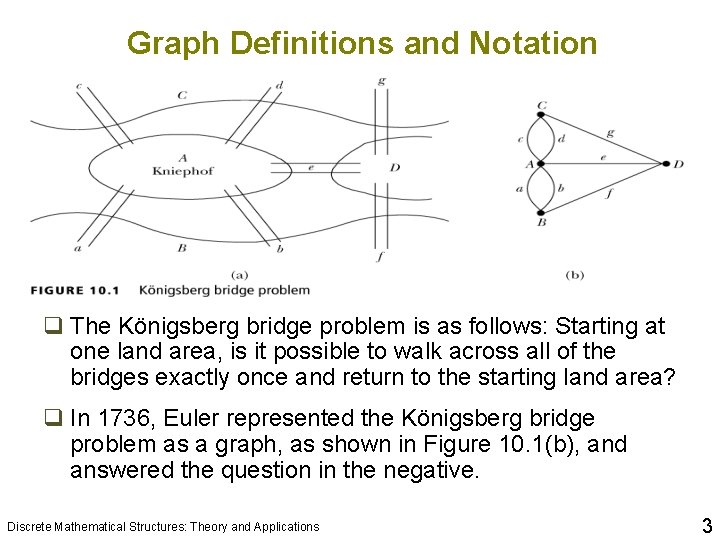
Graph Definitions and Notation 10 q The Königsberg bridge problem is as follows: Starting at one land area, is it possible to walk across all of the bridges exactly once and return to the starting land area? q In 1736, Euler represented the Königsberg bridge problem as a graph, as shown in Figure 10. 1(b), and answered the question in the negative. Discrete Mathematical Structures: Theory and Applications 3

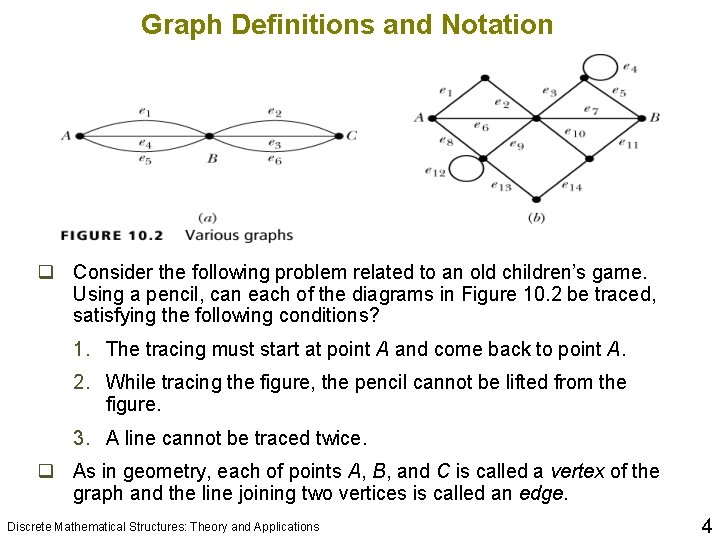
Graph Definitions and Notation 10 q Consider the following problem related to an old children’s game. Using a pencil, can each of the diagrams in Figure 10. 2 be traced, satisfying the following conditions? 1. The tracing must start at point A and come back to point A. 2. While tracing the figure, the pencil cannot be lifted from the figure. 3. A line cannot be traced twice. q As in geometry, each of points A, B, and C is called a vertex of the graph and the line joining two vertices is called an edge. Discrete Mathematical Structures: Theory and Applications 4

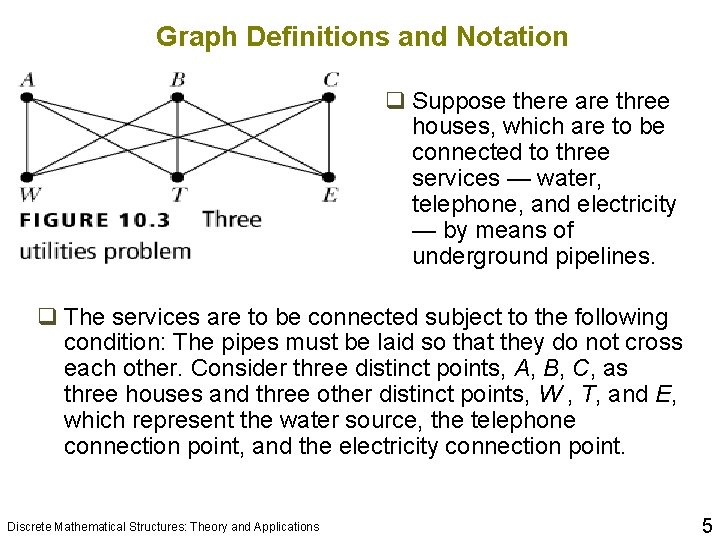
Graph Definitions and Notation 10 q Suppose there are three houses, which are to be connected to three services — water, telephone, and electricity — by means of underground pipelines. q The services are to be connected subject to the following condition: The pipes must be laid so that they do not cross each other. Consider three distinct points, A, B, C, as three houses and three other distinct points, W , T, and E, which represent the water source, the telephone connection point, and the electricity connection point. Discrete Mathematical Structures: Theory and Applications 5

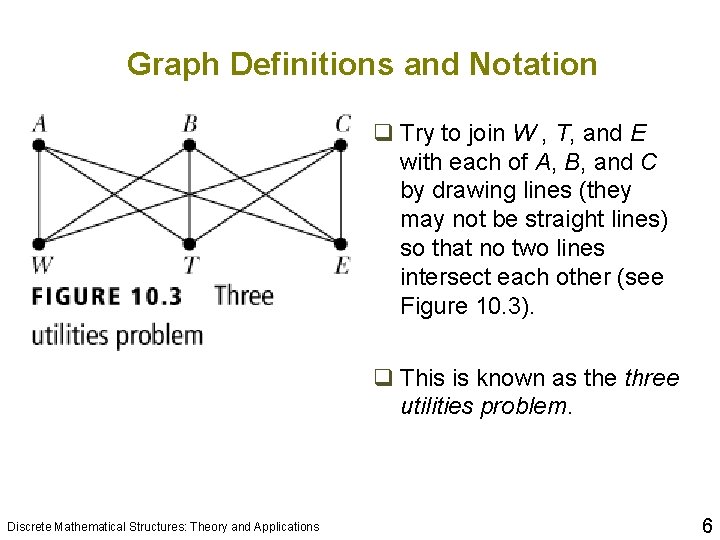
Graph Definitions and Notation 10 q Try to join W , T, and E with each of A, B, and C by drawing lines (they may not be straight lines) so that no two lines intersect each other (see Figure 10. 3). q This is known as the three utilities problem. Discrete Mathematical Structures: Theory and Applications 6

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 7

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 8

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 9

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 10

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 11

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 12

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 13

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 14

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 15

Graph Definitions and Notation 10 Discrete Mathematical Structures: Theory and Applications 16

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 17

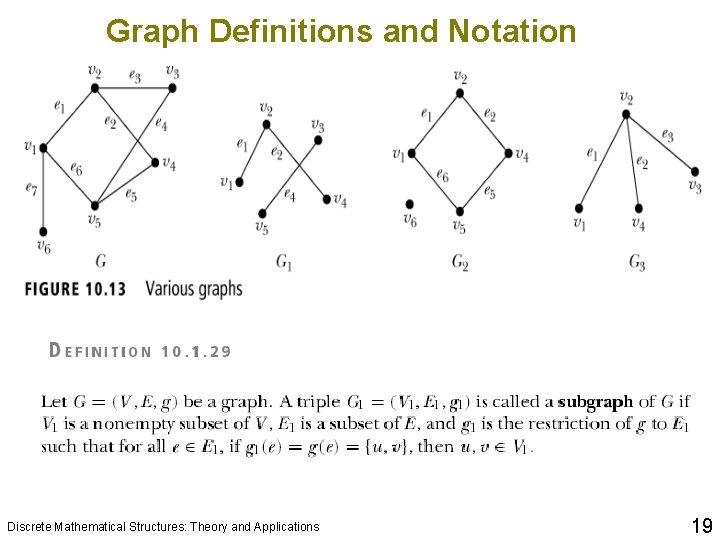
Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 18

Graph Definitions and Notation Discrete Mathematical Structures: Theory and Applications 10 19

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 20

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 21

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 22

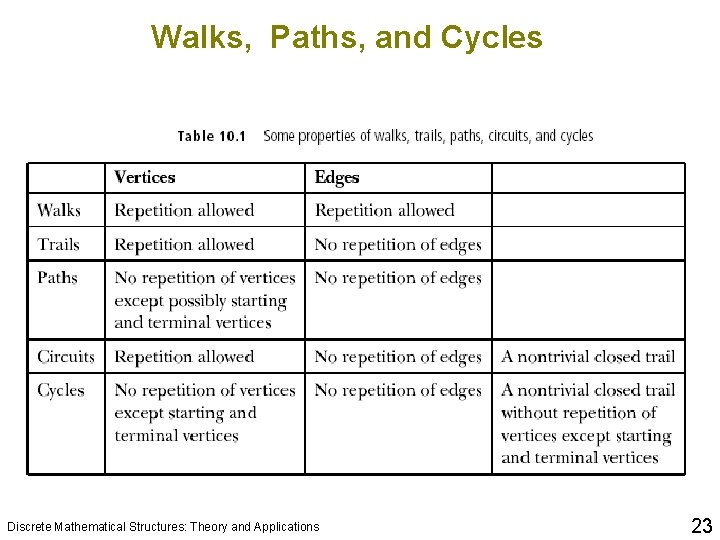
Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 23

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 24

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 25

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 26

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 27

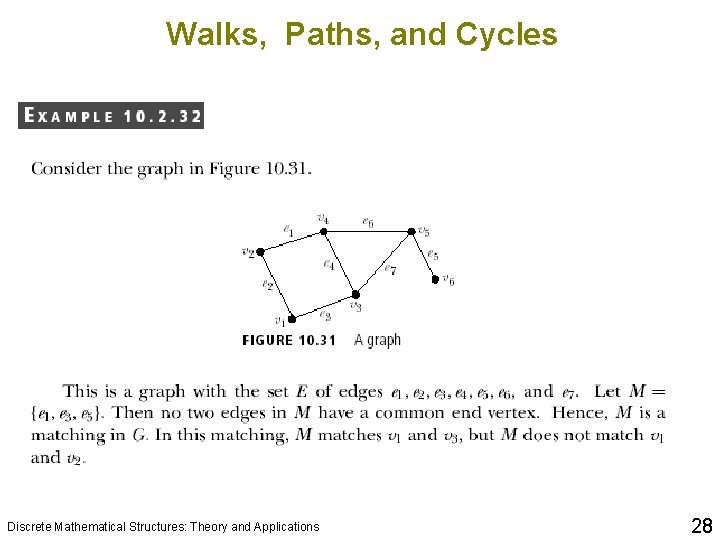
Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 28

Walks, Paths, and Cycles Discrete Mathematical Structures: Theory and Applications 10 29