Lecture 14 Example circuits Zener diodes dependent sources

Lecture #14 Example circuits, Zener diodes, dependent sources, basic amplifiers Reading: 4. 10, 5. 1, 5. 8 Next: transistors (chapter 6 and 14) 10/1/2004 EE 42 fall 2004 lecture 14 1

Topics Today: Examples, circuit applications: • Diode circuits, Zener diode • Use of dependent sources • Basic Amplifier Models 10/1/2004 EE 42 fall 2004 lecture 14 2

Notes on Use of Models • Most of the diode models are piecewise defined: – – One function for reverse bias Another forward bias • You will need to: – “Guess” which diode or diodes are reverse (or forward) biased – Solve for V, I according to your guess – If result is impossible, guess again • Rarely, both guesses may lead to impossibility. – 10/1/2004 Then you must use a more detailed model EE 42 fall 2004 lecture 14 3

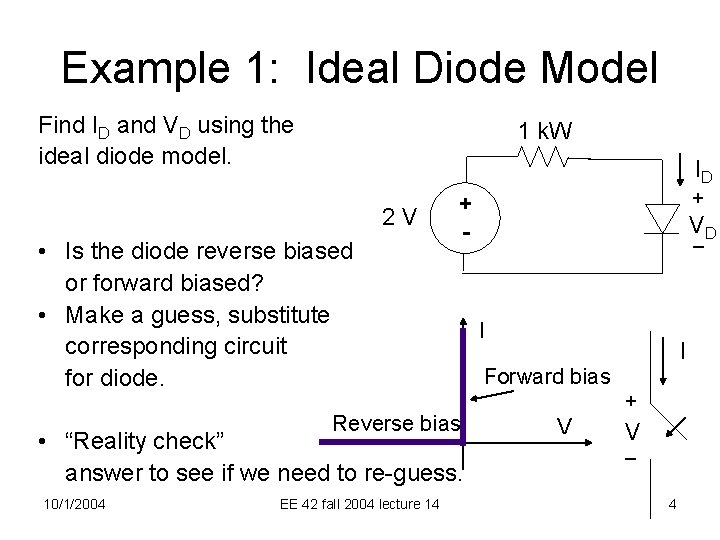
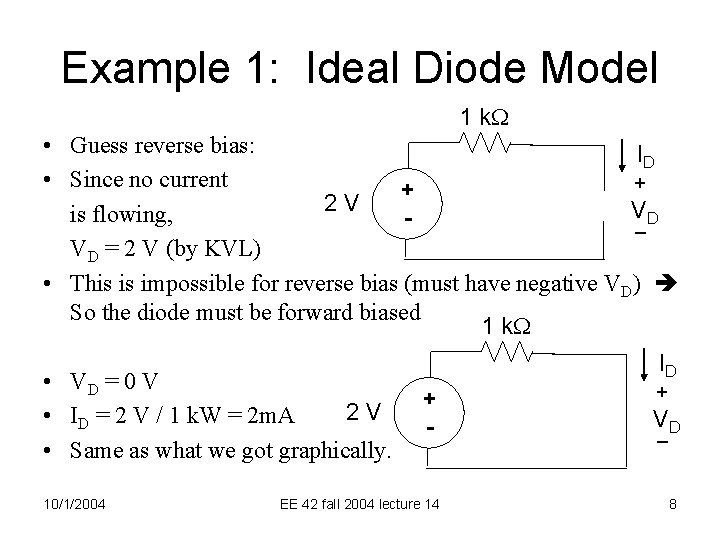
Example 1: Ideal Diode Model Find ID and VD using the ideal diode model. 1 k. W ID 2 V • Is the diode reverse biased or forward biased? • Make a guess, substitute corresponding circuit for diode. Reverse bias • “Reality check” answer to see if we need to re-guess. 10/1/2004 EE 42 fall 2004 lecture 14 + + - V _D I I Forward bias + V V _ 4

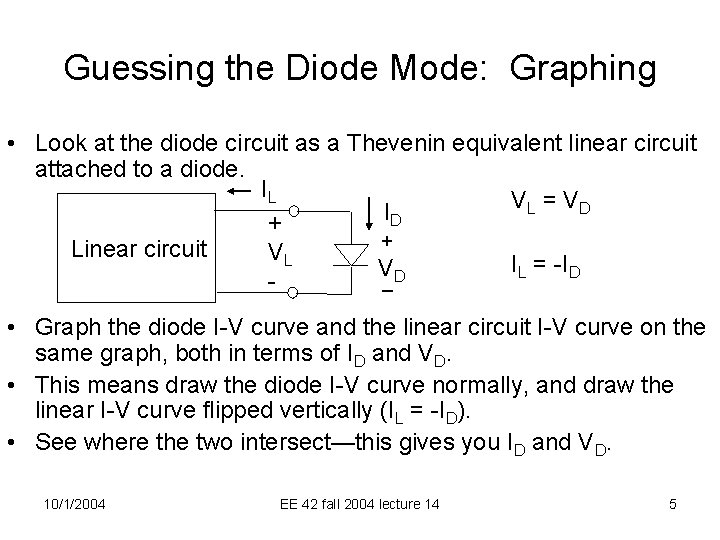
Guessing the Diode Mode: Graphing • Look at the diode circuit as a Thevenin equivalent linear circuit attached to a diode. IL VL = V D I D + + Linear circuit VL IL = -ID V D _ • Graph the diode I-V curve and the linear circuit I-V curve on the same graph, both in terms of ID and VD. • This means draw the diode I-V curve normally, and draw the linear I-V curve flipped vertically (IL = -ID). • See where the two intersect—this gives you ID and VD. 10/1/2004 EE 42 fall 2004 lecture 14 5

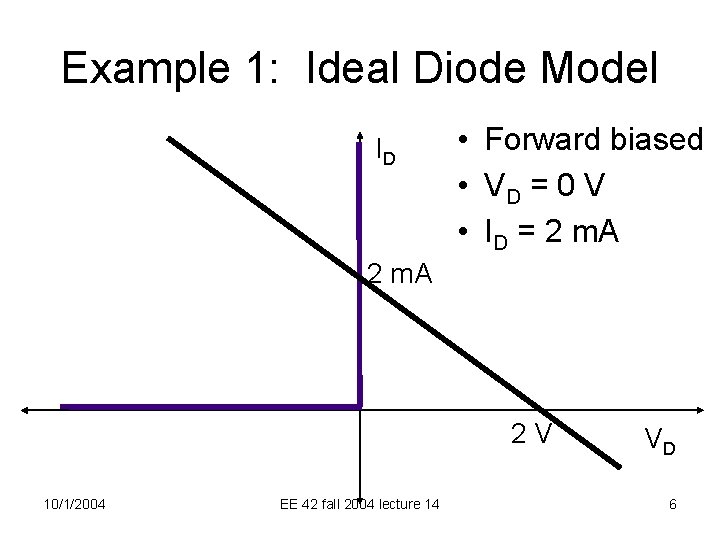
Example 1: Ideal Diode Model ID • Forward biased • VD = 0 V • ID = 2 m. A 2 V 10/1/2004 EE 42 fall 2004 lecture 14 VD 6

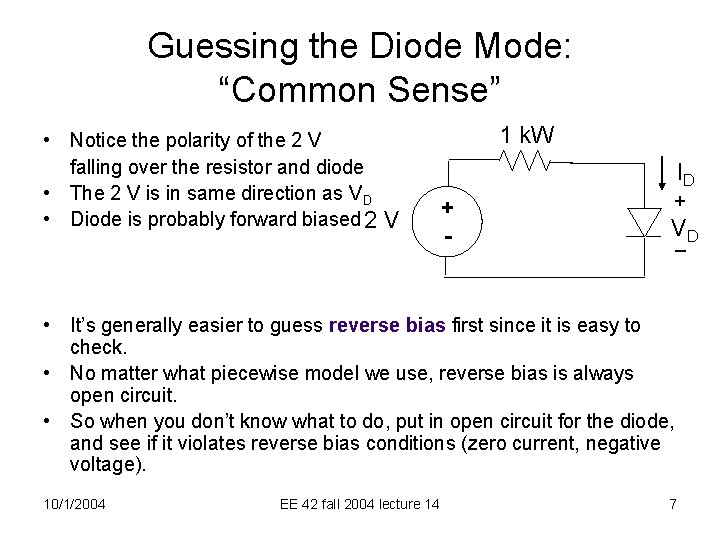
Guessing the Diode Mode: “Common Sense” • Notice the polarity of the 2 V falling over the resistor and diode • The 2 V is in same direction as VD • Diode is probably forward biased 2 V 1 k. W ID + - + V _D • It’s generally easier to guess reverse bias first since it is easy to check. • No matter what piecewise model we use, reverse bias is always open circuit. • So when you don’t know what to do, put in open circuit for the diode, and see if it violates reverse bias conditions (zero current, negative voltage). 10/1/2004 EE 42 fall 2004 lecture 14 7

Example 1: Ideal Diode Model 1 k. W • Guess reverse bias: ID • Since no current + + 2 V V is flowing, _D VD = 2 V (by KVL) • This is impossible for reverse bias (must have negative VD) So the diode must be forward biased 1 k. W • VD = 0 V 2 V • ID = 2 V / 1 k. W = 2 m. A • Same as what we got graphically. 10/1/2004 ID + + - V _D EE 42 fall 2004 lecture 14 8

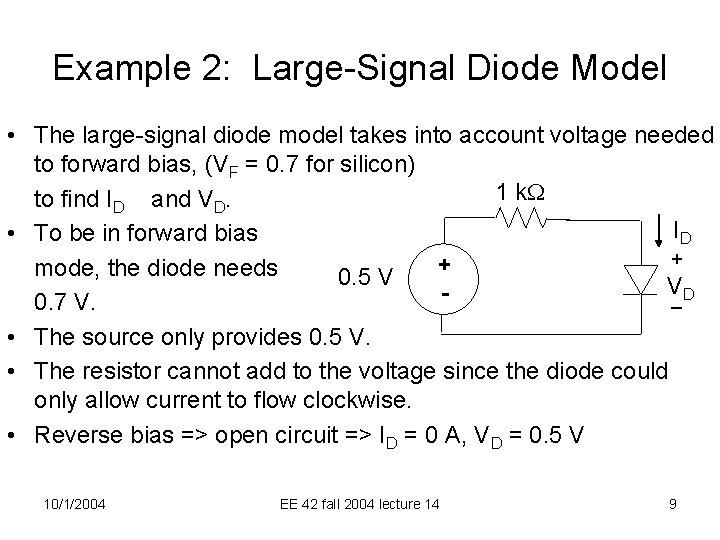
Example 2: Large-Signal Diode Model • The large-signal diode model takes into account voltage needed to forward bias, (VF = 0. 7 for silicon) 1 k. W to find ID and VD. ID • To be in forward bias + + mode, the diode needs 0. 5 V V _D 0. 7 V. • The source only provides 0. 5 V. • The resistor cannot add to the voltage since the diode could only allow current to flow clockwise. • Reverse bias => open circuit => ID = 0 A, VD = 0. 5 V 10/1/2004 EE 42 fall 2004 lecture 14 9

Zener diodes • A Zener diode is the name commonly used for a diode which is designed for use in reverse breakdown • Since the diode breaks down sharply, at accurate voltage, it can be used as a voltage reference • The symbol for a Zener diode: 10/1/2004 EE 42 fall 2004 lecture 14 10

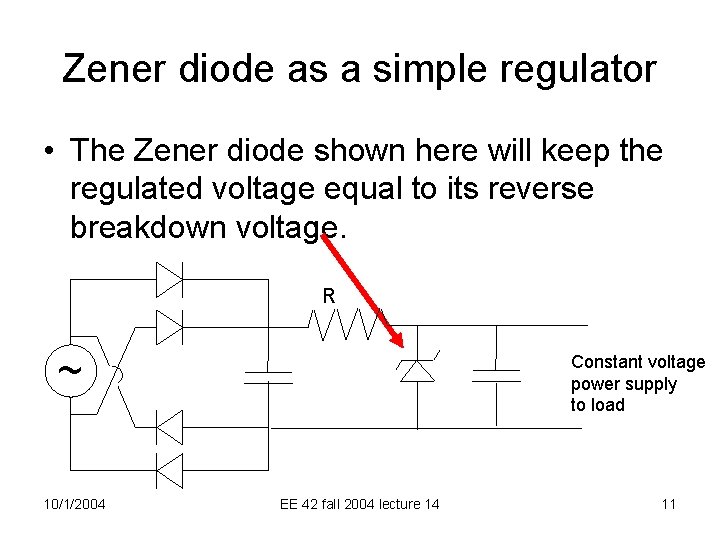
Zener diode as a simple regulator • The Zener diode shown here will keep the regulated voltage equal to its reverse breakdown voltage. R ~ 10/1/2004 Constant voltage power supply to load EE 42 fall 2004 lecture 14 11

Resistor sizing • How big should R be in the regulator shown? • If the load draws a current I, then the resistor must carry that current when the unregulated voltage is at the lowest point, without letting the regulated voltage drop. • Lets say the load draws 10 milliamps, the regulated voltage is 2 volts, and the minimum unregulated voltage (low point of ripple) is 2. 5 volts) • The resistor must be • R=(2. 5 v-2 v)/10 milliamps=500 ohms. 10/1/2004 EE 42 fall 2004 lecture 14 12

Ripple calculation • How much ripple will be observed on the unregulated supply? • The maximum current will be: • And we can estimate the amount of charge lost: • So the ripple will be 10/1/2004 EE 42 fall 2004 lecture 14 13

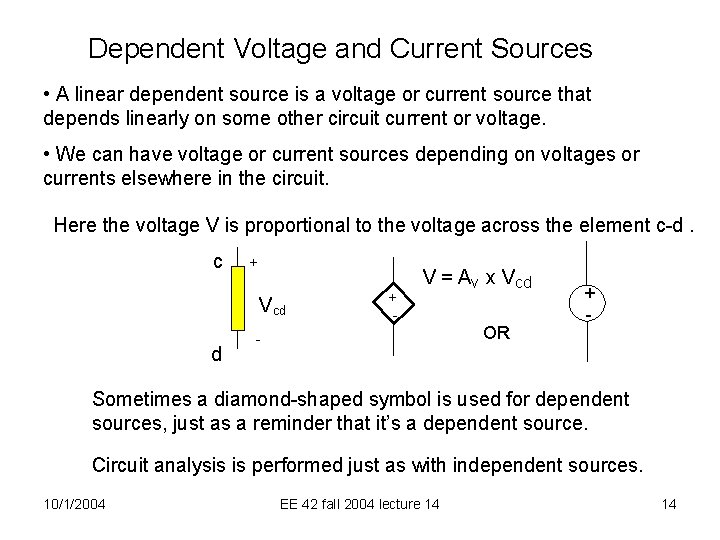
Dependent Voltage and Current Sources • A linear dependent source is a voltage or current source that depends linearly on some other circuit current or voltage. • We can have voltage or current sources depending on voltages or currents elsewhere in the circuit. Here the voltage V is proportional to the voltage across the element c-d. c + Vcd d + - V = Av x Vcd OR - + - Sometimes a diamond-shaped symbol is used for dependent sources, just as a reminder that it’s a dependent source. Circuit analysis is performed just as with independent sources. 10/1/2004 EE 42 fall 2004 lecture 14 14

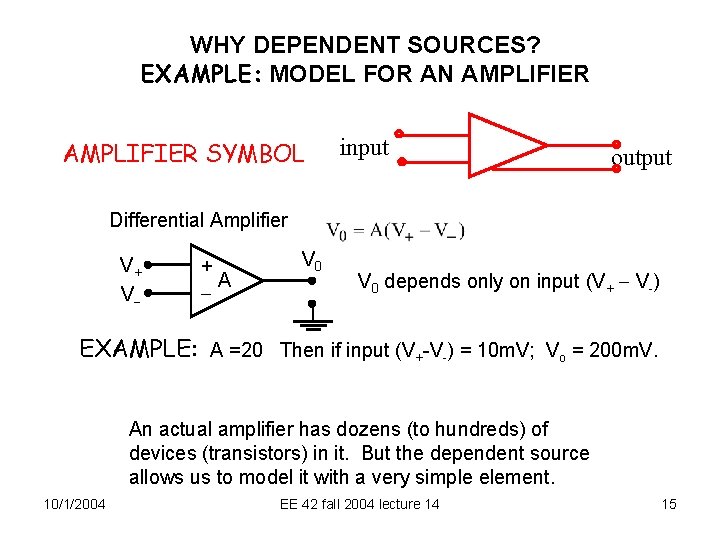
WHY DEPENDENT SOURCES? EXAMPLE: MODEL FOR AN AMPLIFIER SYMBOL input output Differential Amplifier V+ V + A V 0 depends only on input (V+ V-) EXAMPLE: A =20 Then if input (V+-V-) = 10 m. V; Vo = 200 m. V. An actual amplifier has dozens (to hundreds) of devices (transistors) in it. But the dependent source allows us to model it with a very simple element. 10/1/2004 EE 42 fall 2004 lecture 14 15

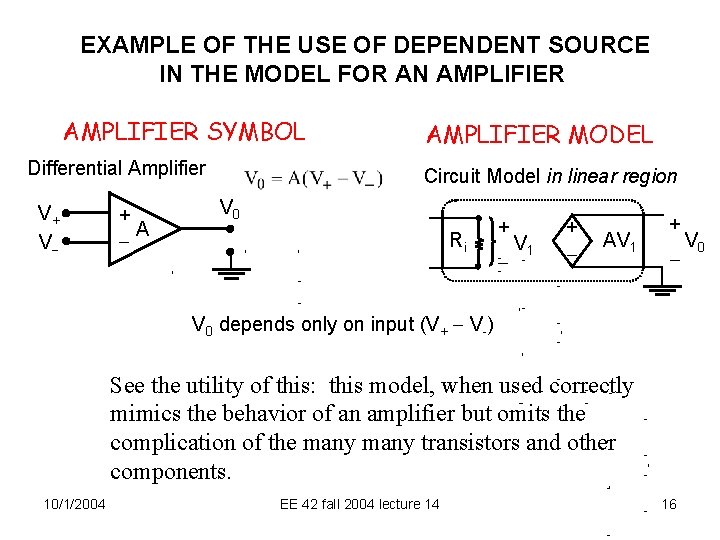
EXAMPLE OF THE USE OF DEPENDENT SOURCE IN THE MODEL FOR AN AMPLIFIER SYMBOL Differential Amplifier V+ V + A AMPLIFIER MODEL Circuit Model in linear region V 0 Ri + V 1 + AV 1 + V 0 depends only on input (V+ V-) See the utility of this: this model, when used correctly mimics the behavior of an amplifier but omits the complication of the many transistors and other components. 10/1/2004 EE 42 fall 2004 lecture 14 16 V 0

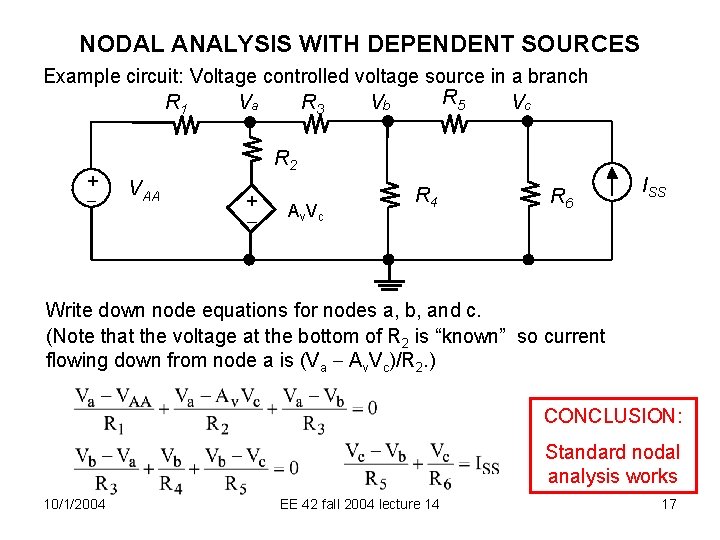
NODAL ANALYSIS WITH DEPENDENT SOURCES Example circuit: Voltage controlled voltage source in a branch R 1 + R 3 Va R 5 Vb Vc R 2 VAA + Av Vc R 4 R 6 ISS Write down node equations for nodes a, b, and c. (Note that the voltage at the bottom of R 2 is “known” so current flowing down from node a is (Va Av. Vc)/R 2. ) CONCLUSION: Standard nodal analysis works 10/1/2004 EE 42 fall 2004 lecture 14 17

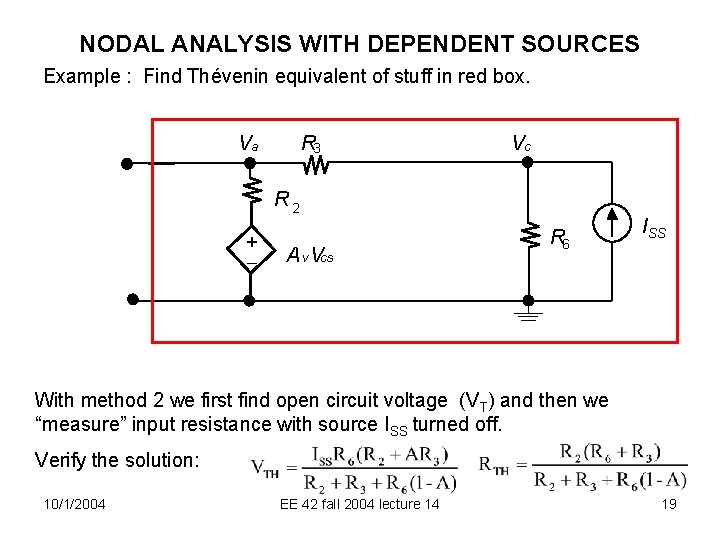
NODAL ANALYSIS WITH DEPENDENT SOURCES Finding Thévenin Equivalent Circuits with Dependent Sources Present Method 1: Use Voc and Isc as usual to find VT and RT (and IN as well) Method 2: To find RT by the “ohmmeter method” turn off only the independent sources; let the dependent sources just do their thing. See examples in text (such as Example 4. 3) and in discussion sections. Pay most attention to voltage-dependent voltage sources and voltage-dependent current sources. We will use these only. 10/1/2004 EE 42 fall 2004 lecture 14 18

NODAL ANALYSIS WITH DEPENDENT SOURCES Example : Find Thévenin equivalent of stuff in red box. R 3 Va Vc R 2 + A v Vcs R 6 ISS With method 2 we first find open circuit voltage (VT) and then we “measure” input resistance with source ISS turned off. Verify the solution: 10/1/2004 EE 42 fall 2004 lecture 14 19

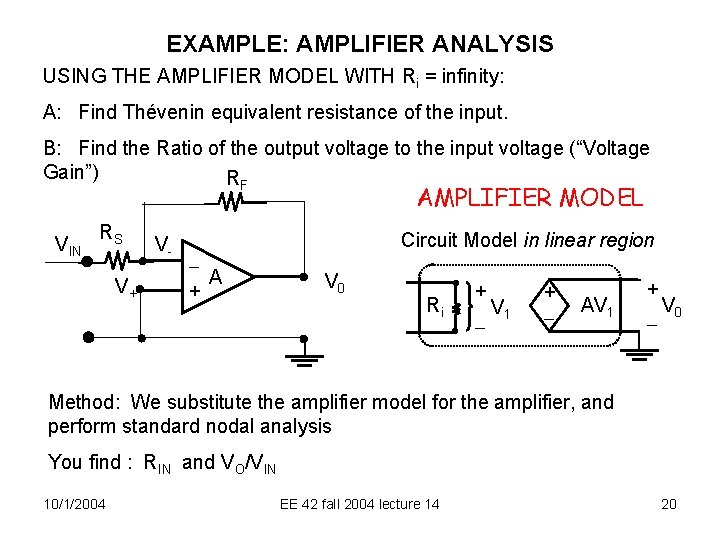
EXAMPLE: AMPLIFIER ANALYSIS USING THE AMPLIFIER MODEL WITH Ri = infinity: A: Find Thévenin equivalent resistance of the input. B: Find the Ratio of the output voltage to the input voltage (“Voltage Gain”) R F VIN RS V+ V- AMPLIFIER MODEL Circuit Model in linear region A + V 0 Ri + V 1 + AV 1 + V 0 Method: We substitute the amplifier model for the amplifier, and perform standard nodal analysis You find : RIN and VO/VIN 10/1/2004 EE 42 fall 2004 lecture 14 20

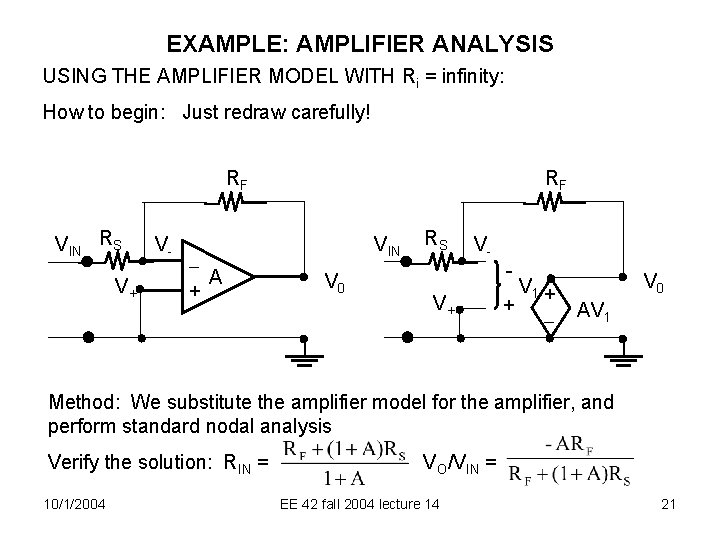
EXAMPLE: AMPLIFIER ANALYSIS USING THE AMPLIFIER MODEL WITH Ri = infinity: How to begin: Just redraw carefully! RF VIN RS V+ V- A + RF VIN V 0 RS V- V+ + V 1 + V 0 AV 1 Method: We substitute the amplifier model for the amplifier, and perform standard nodal analysis Verify the solution: RIN = 10/1/2004 VO/VIN = EE 42 fall 2004 lecture 14 21