Lecture 13 Rotational Kinetic Energy and Rotational Inertia

Lecture 13: Rotational Kinetic Energy and Rotational Inertia Review: Rotational Kinematics l Rotational Kinetic Energy l Rotational Inertia l Torque l Rotational Dynamics l Equilibrium l

Recall: Rotational Kinematics Angular Linear And for a point at a distance R from the rotation axis: x. T = R v. T= R a. T = R

Comment on Axes and Signs (i. e. what is positive and negative) l. Whenever we talk about rotation, it is implied that there is a rotation “axis”. l. This is usually called the “z” axis (we usually omit the z subscript for simplicity). l. Counter-clockwise called positive. (increasing ) is usually z (decreasing ) is usually called negative. l. Clockwise +

Rotational Kinetic Energy l Consider a mass M on the end of a string being spun around in a circle with radius R and angular frequency . èMass has speed v = R èMass has kinetic energy » K = ½ M v 2 » K = ½ M 2 r 2 l Rotational Kinetic Energy is energy due to circular motion of object. M

Kinetic Energy of Rotating Disk l Consider a disk with radius R and mass M, spinning with angular frequency . èEach “piece” of disk has speed vi= ri èEach “piece” has kinetic energy » Ki = ½ mi v 2 » = ½ m i 2 ri èCombine all the pieces » Ki = ½ mi 2 r 2 » = ½ ( mi ri 2) 2 » = ½ I 2 I is called the Rotational Inertia

Rotational Inertia I l Tells how much “work” is required to get object spinning. Just like mass tells you how much “work” is required to get object moving. èKtran = ½ m v 2 Linear Motion èKrot = ½ I 2 l I m i ri 2 l Note! Rotational Motion (units kg-m 2) Rotational Inertia depends on what axis you are spinning about (the ri in the equation).

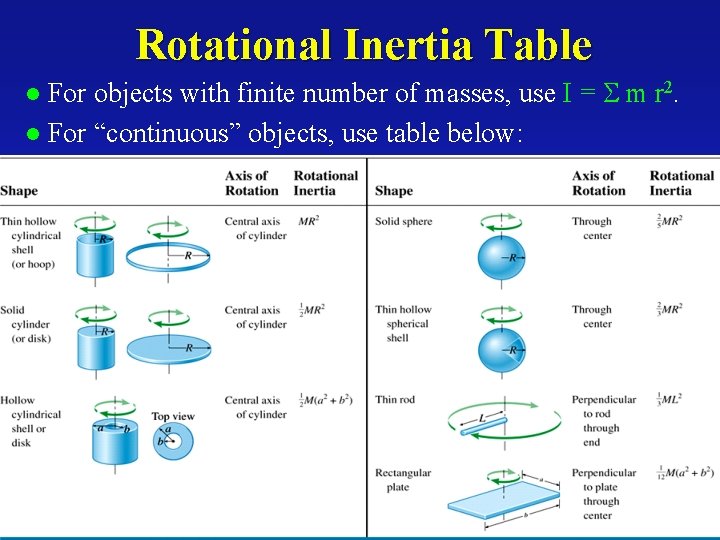
Rotational Inertia Table For objects with finite number of masses, use I = m r 2. l For “continuous” objects, use table below: l

Summary l Rotational Kinetic Energy Krot = ½ I 2 l Rotational Inertia I = miri 2 l Energy is Still Conserved!

Pulley Example l A solid disk wheel is fixed at its center and has a string wrapped around it and then attached to a block. The mass of the pulley is 5 kg, the radius of the pulley is 0. 2 m, and the mass of the block is 8 kg. After the block has fallen 1. 5 m, how fast is the block moving and how fast is the disk rotating? èWe will use conservation of energy: 5 kg èRemember: » Ktrans = ½ m v 2 » Krot= ½ I 2 » U=mgy 8 kg 1. 5 m

Pulley Example l A solid disk wheel is fixed at its center and has a string wrapped around it and then attached to a block. The mass of the pulley is 5 kg, the radius of the pulley is 0. 2 m, and the mass of the block is 8 kg. After the block has fallen 1. 5 m, how fast is the block moving and how fast is the disk rotating? èInitial Krot and Ktran is zero. 5 kg èFinal U is zero. 8 kg 1. 5 m

Pulley Example l A solid disk wheel is fixed at its center and has a string wrapped around it and then attached to a block. The mass of the pulley is 5 kg, the radius of the pulley is 0. 2 m, and the mass of the block is 8 kg. After the block has fallen 1. 5 m, how fast is the block moving and how fast is the disk rotating? èRemember: 5 kg » I = ½ m R 2 for a disk » v = R so = v/R 8 kg 1. 5 m

Pulley Example l A solid disk wheel is fixed at its center and has a string wrapped around it and then attached to a block. The mass of the pulley is 5 kg, the radius of the pulley is 0. 2 m, and the mass of the block is 8 kg. After the block has fallen 1. 5 m, how fast is the block moving and how fast is the disk rotating? èR 2 cancels from the last term. 5 kg 8 kg èSimplify: 1. 5 m

Pulley Example l A solid disk wheel is fixed at its center and has a string wrapped around it and then attached to a block. The mass of the pulley is 5 kg, the radius of the pulley is 0. 2 m, and the mass of the block is 8 kg. After the block has fallen 1. 5 m, how fast is the block moving and how fast is the disk rotating? 5 kg èSolve: vf = 4. 73 m/s 8 kg 1. 5 m

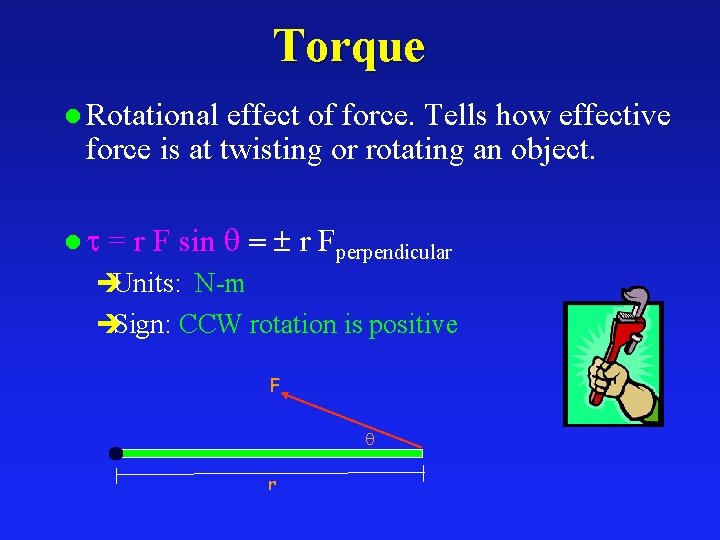
Torque l Rotational effect of force. Tells how effective force is at twisting or rotating an object. l = r F sin = r Fperpendicular èUnits: N-m èSign: CCW rotation is positive F r

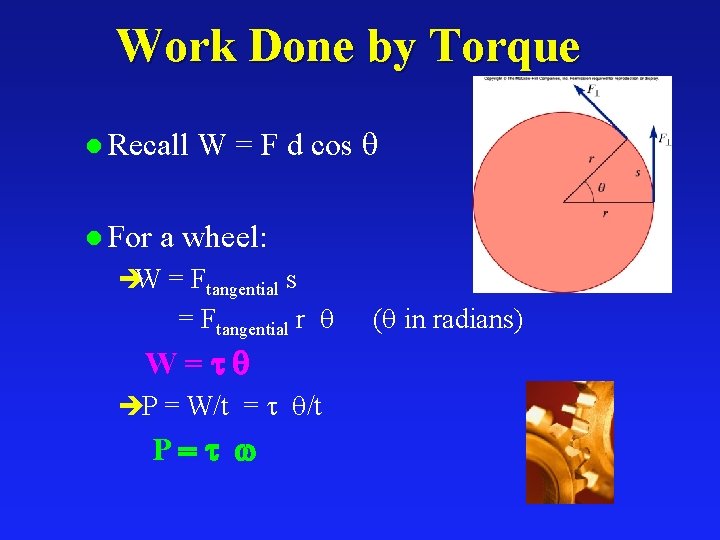
Work Done by Torque l Recall l For W = F d cos a wheel: èW = Ftangential s = Ftangential r W=tq è P = W/t = /t P = t w ( in radians)

Equilibrium l Conditions è F = 0 for Equilibrium: Translational Equilibrium (Center of Mass) Rotational Equilibrium è = 0 » May choose any axis of rotation…. But Choose Wisely!

Equilibrium Example l A 50 kg diver stands at the end of a 4. 6 m diving board. Neglecting the weight of the board, what is the force each pivot exerts on the diving board? èFirst, draw a FBD: F 1 F 2 Fg

Equilibrium Example l A 50 kg diver stands at the end of a 4. 6 m diving board. Neglecting the weight of the board, what is the force each pivot exerts on the diving board? èWrite down F = 0: -F 1 + F 2 – Fg = 0 -F 1 + F 2 – (50 kg)(9. 8 m/s 2) = 0 Note: there are two unknowns so we need another equation…

Equilibrium Example l A 50 kg diver stands at the end of a 4. 6 m diving board. Neglecting the weight of the board, what is the force each pivot exerts on the diving board? èPick a pivot point: F 1 F 2 Fg

Equilibrium Example l A 50 kg diver stands at the end of a 4. 6 m diving board. Neglecting the weight of the board, what is the force each pivot exerts on the diving board? èWrite down = 0: F 1 (0 m) + F 2 (1. 2 m) – (50 kg)(9. 8 m/s 2)(4. 6 m) = 0

Equilibrium Example l A 50 kg diver stands at the end of a 4. 6 m diving board. Neglecting the weight of the board, what is the force each pivot exerts on the diving board? èSolve: F 2 (1. 2 m) – (50 kg)(9. 8 m/s 2)(4. 6 m) = 0 F 2 = 1878 N -F 1 + F 2 – (50 kg)(9. 8 m/s 2) = 0 -F 1 + (1878 N) – (50 kg)(9. 8 m/s 2) = 0 F 1 = 1388 N

Summary l Torque is a Force that causes rotation è = F r sin èWork done by torque: W = l Equilibrium è F = 0 è = 0 » May choose any axis.