Lecture 13 Introduction to Minimum Cost Flows A

  • Slides: 44
Download presentation
Lecture 13 Introduction to Minimum Cost Flows

Lecture 13 Introduction to Minimum Cost Flows

A feasible flow x is optimal for the minimum cost flow problem if and

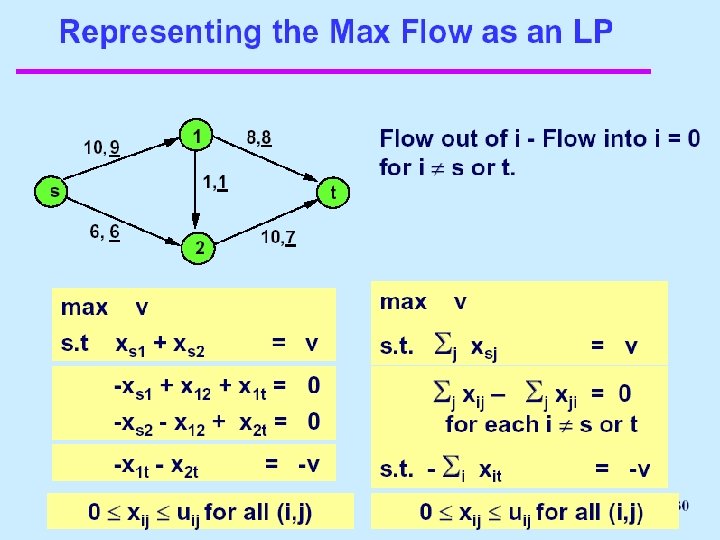
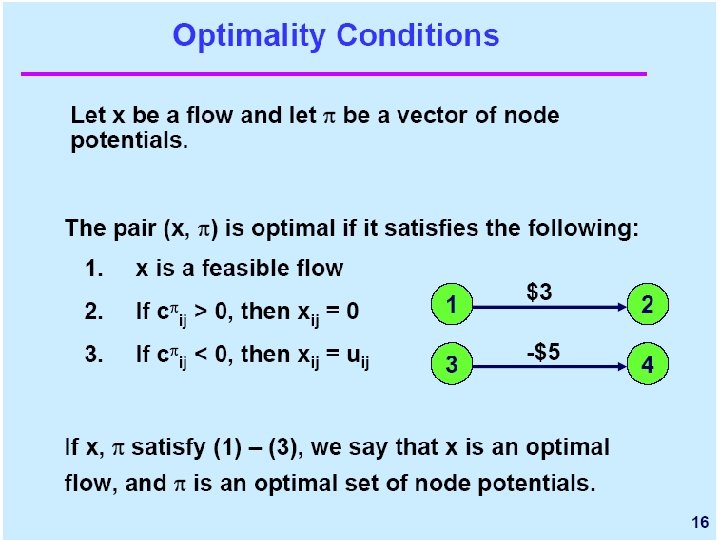
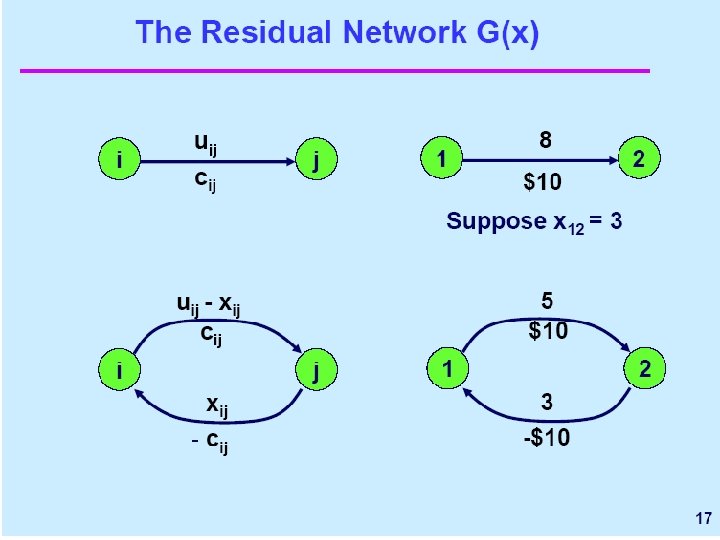
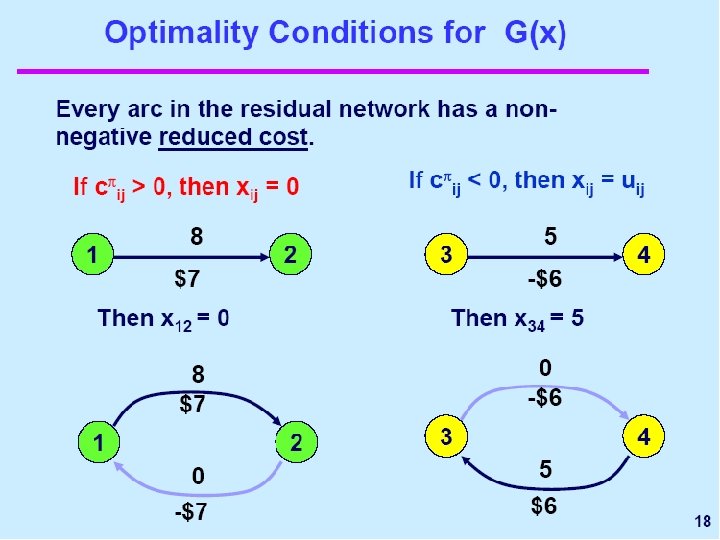
A feasible flow x is optimal for the minimum cost flow problem if and only if some set of node potentials satisfy the following reduced cost optimality conditions: for every arc (i, j) in G(x),

Cycle Canceling Algorithm

Cycle Canceling Algorithm

A minimum cost flow problem 0 2 10, $4 0 4 30, $7 25

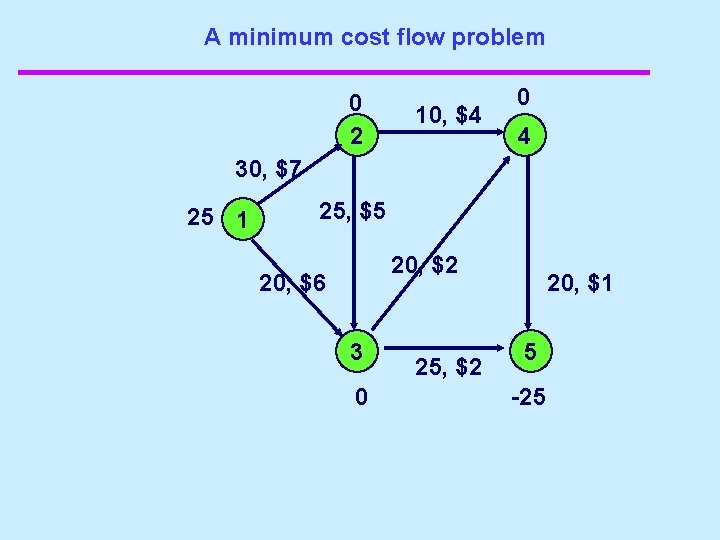
A minimum cost flow problem 0 2 10, $4 0 4 30, $7 25 1 25, $5 20, $2 20, $6 3 0 25, $2 20, $1 5 -25

The Original Capacities and Feasible Flow 0 2 0 10, 10 4 30, 25

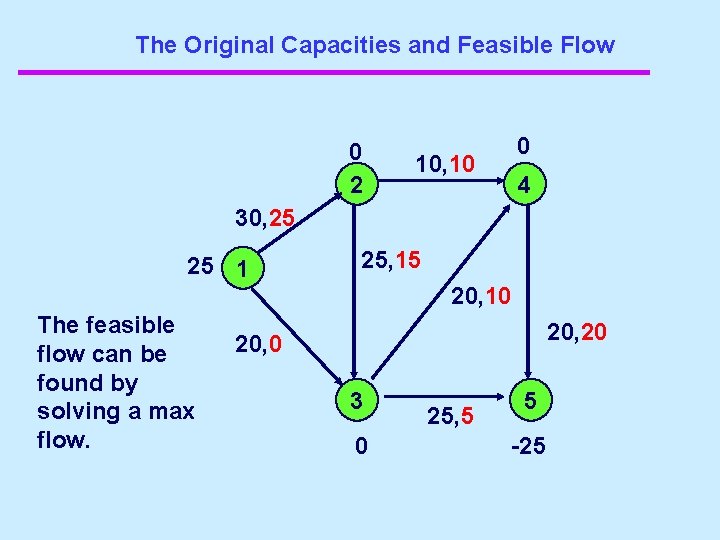
The Original Capacities and Feasible Flow 0 2 0 10, 10 4 30, 25 25 1 25, 15 20, 10 The feasible flow can be found by solving a max flow. 20, 20 20, 0 3 0 25, 5 5 -25

Capacities on the Residual Network 2 10 4 5 1 25 15 10 20

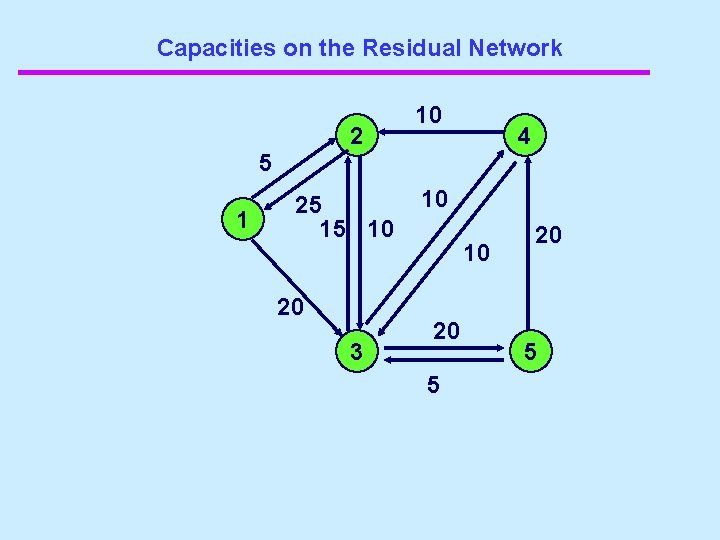
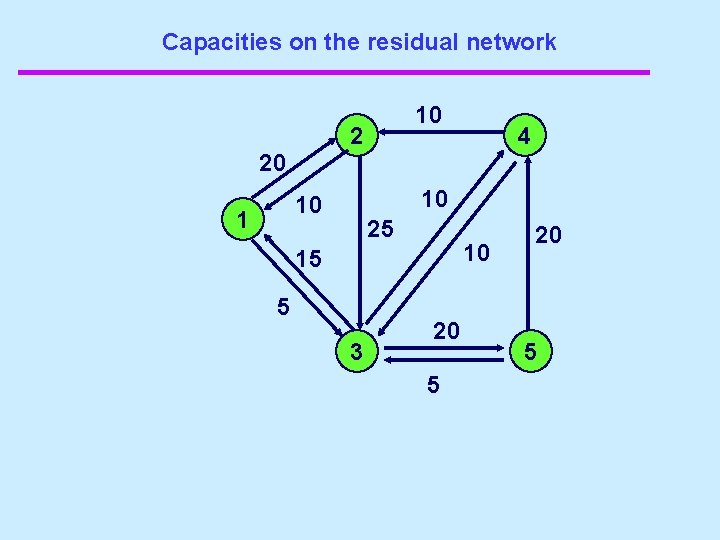
Capacities on the Residual Network 2 10 4 5 1 25 15 10 20 3 10 10 20 5

Costs on the Residual Network 2 -4 7 -7 1 5 -5 6 3

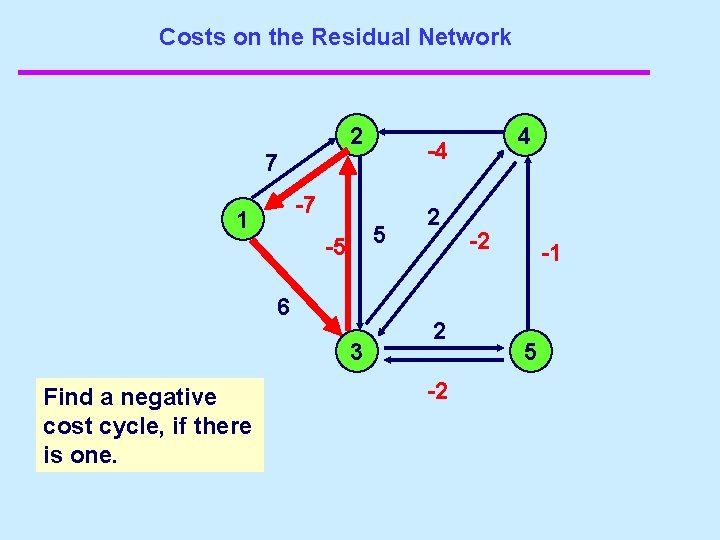
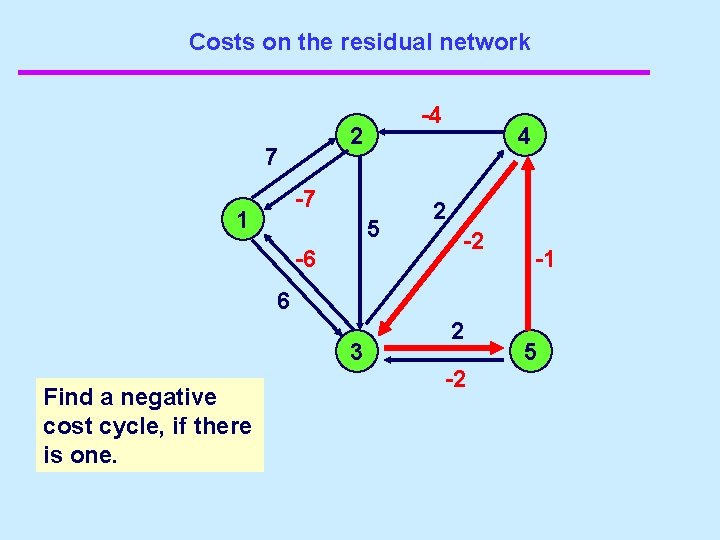
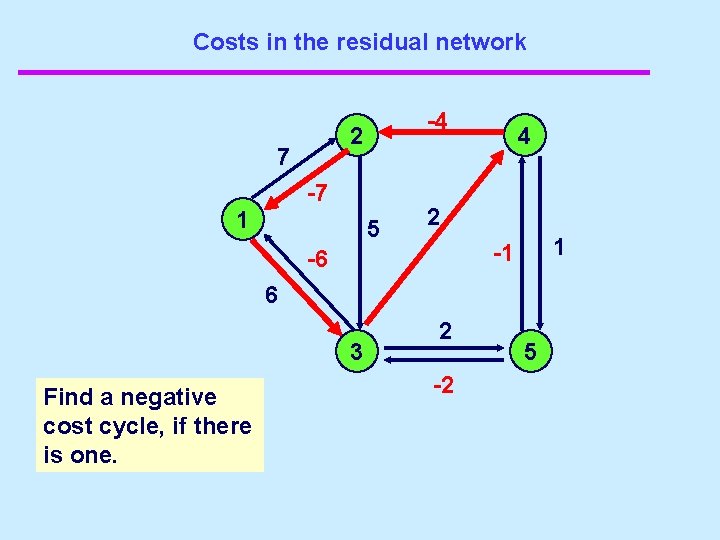
Costs on the Residual Network 2 -4 7 -7 1 5 -5 6 3 Find a negative cost cycle, if there is one. 4 2 2 -2 -2 -1 5

Send flow around the cycle Send flow around the negative cost cycle 1 2

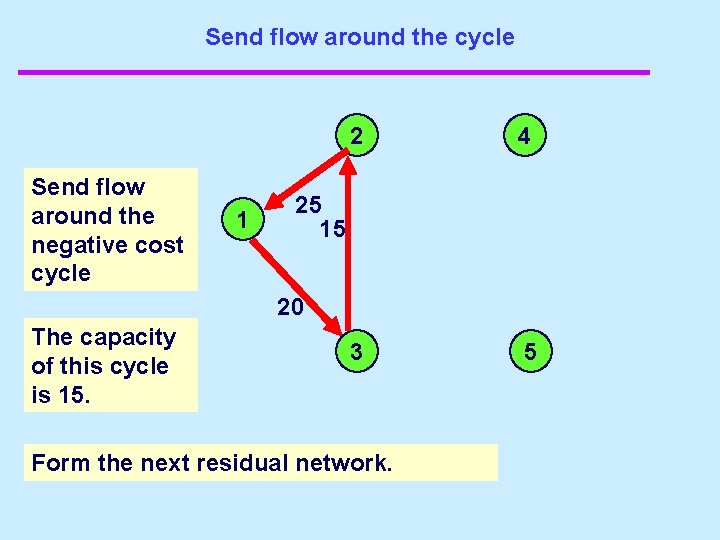
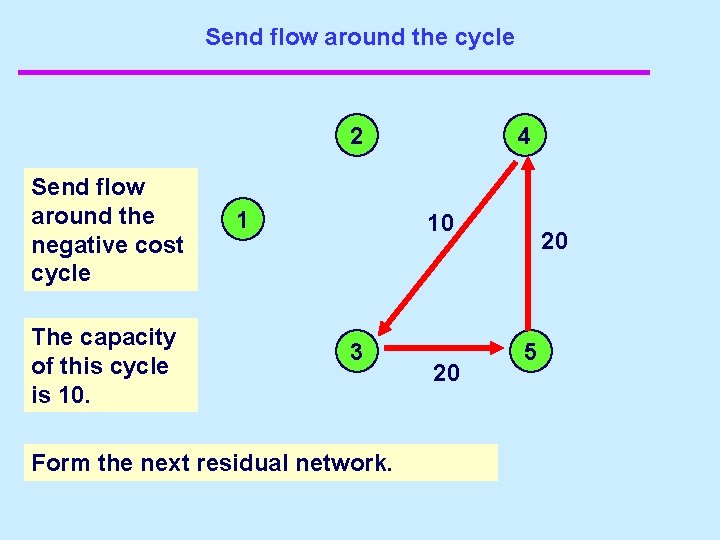
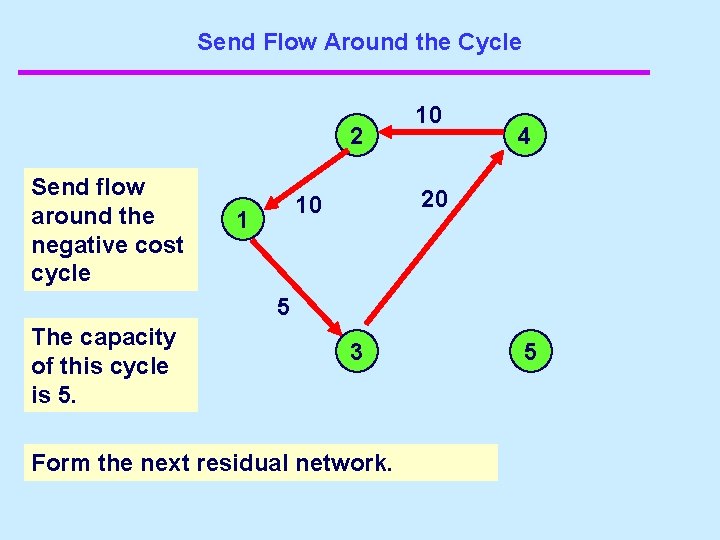
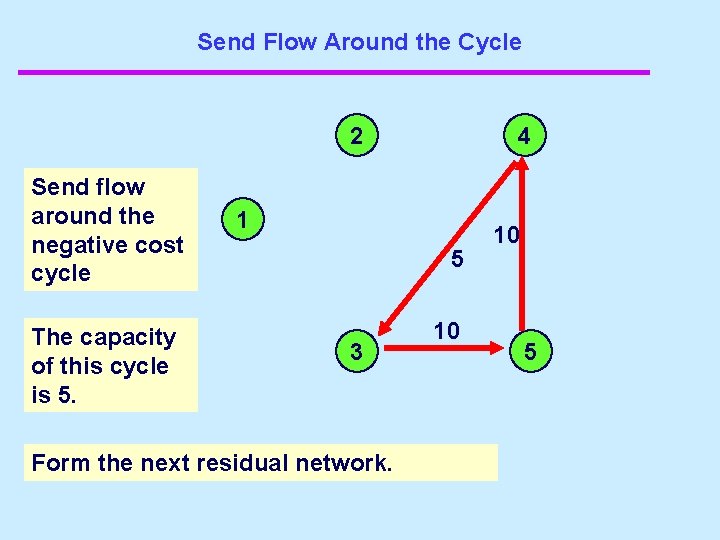
Send flow around the cycle Send flow around the negative cost cycle 1 2 4 3 5 25 15 20 The capacity of this cycle is 15. Form the next residual network.

Capacities on the residual network 10 2 4 20 10 10 1 25 10

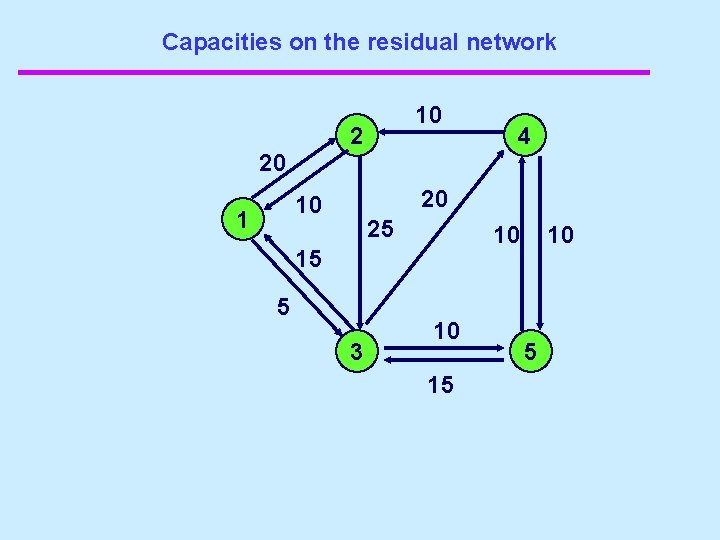
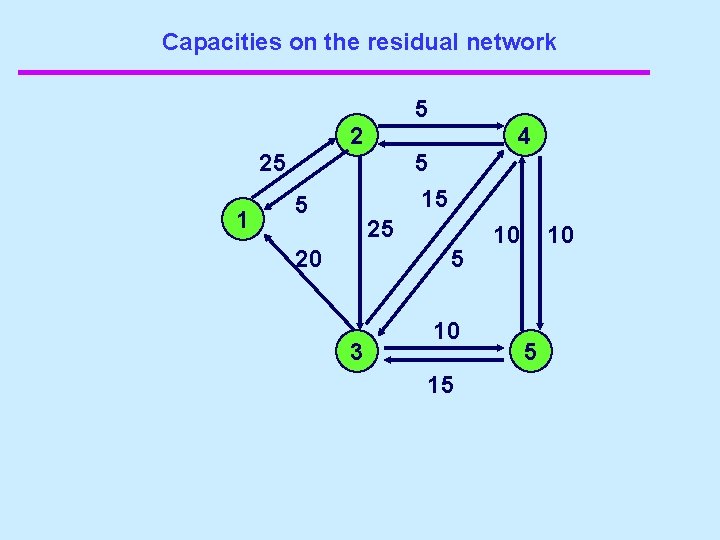
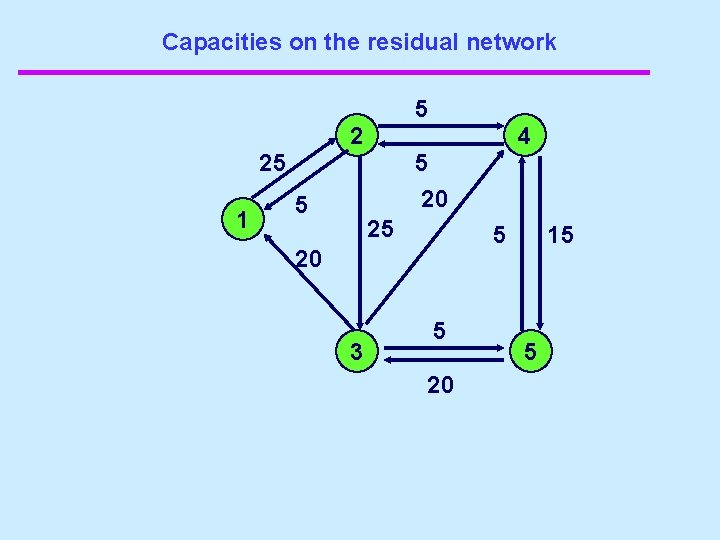
Capacities on the residual network 10 2 4 20 10 10 1 25 10 15 5 3 20 5

Costs on the residual network -4 2 7 -7 1 5 -6 4 2

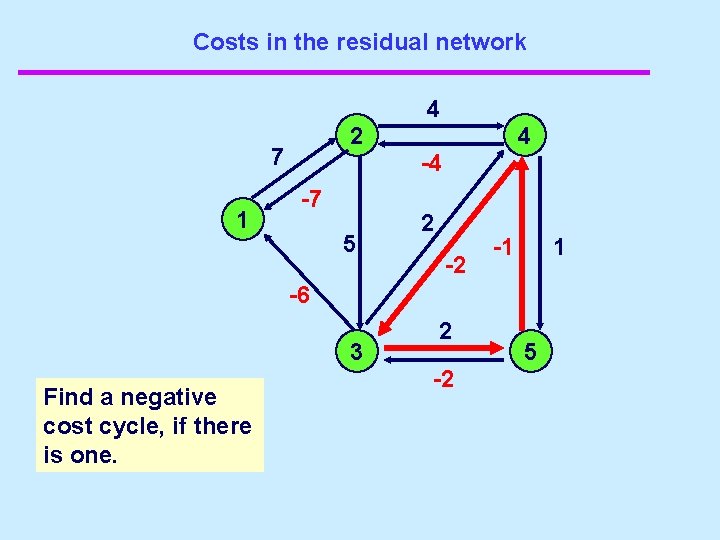
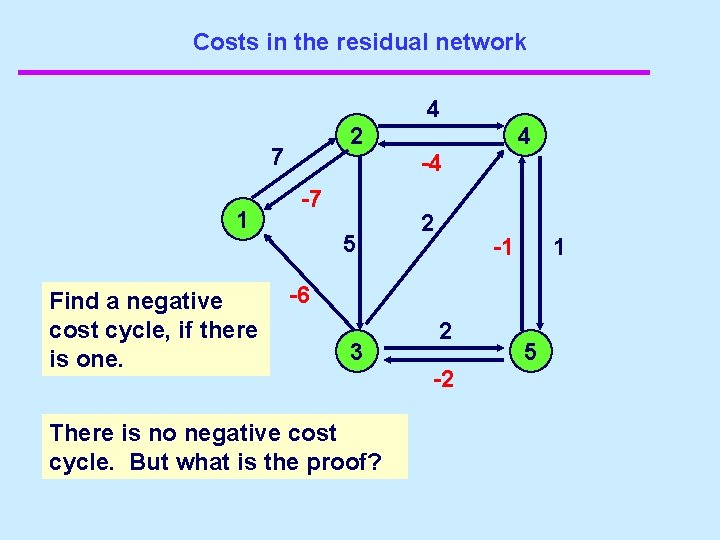
Costs on the residual network -4 2 7 -7 1 5 -6 4 2 -2 -1 6 3 Find a negative cost cycle, if there is one. 2 -2 5

Send flow around the cycle 2 Send flow around the negative cost cycle The

Send flow around the cycle 2 Send flow around the negative cost cycle The capacity of this cycle is 10. 1 4 10 3 Form the next residual network. 20 20 5

Capacities on the residual network 10 2 4 20 20 10 1 25 10

Capacities on the residual network 10 2 4 20 20 10 1 25 10 15 5 3 10 15 10 5

Costs in the residual network -4 2 7 -7 1 5 4 2 1

Costs in the residual network -4 2 7 -7 1 5 4 2 1 -1 -6 6 3 Find a negative cost cycle, if there is one. 2 -2 5

Send Flow Around the Cycle 2 Send flow around the negative cost cycle 4

Send Flow Around the Cycle 2 Send flow around the negative cost cycle 4 20 10 1 10 5 The capacity of this cycle is 5. 3 Form the next residual network. 5

Capacities on the residual network 5 2 4 25 1 5 15 5 25

Capacities on the residual network 5 2 4 25 1 5 15 5 25 20 5 3 10 15 10 10 5

Costs in the residual network 4 2 7 1 4 -4 -7 5 2

Costs in the residual network 4 2 7 1 4 -4 -7 5 2 -2 -1 1 -6 3 Find a negative cost cycle, if there is one. 2 -2 5

Send Flow Around the Cycle 2 Send flow around the negative cost cycle The

Send Flow Around the Cycle 2 Send flow around the negative cost cycle The capacity of this cycle is 5. 4 1 5 3 Form the next residual network. 10 10 5

Capacities on the residual network 5 2 4 25 1 5 20 5 25

Capacities on the residual network 5 2 4 25 1 5 20 5 25 5 20 3 5 20 15 5

Costs in the residual network 4 2 7 1 Find a negative cost cycle,

Costs in the residual network 4 2 7 1 Find a negative cost cycle, if there is one. 4 -4 -7 5 2 -1 1 -6 3 There is no negative cost cycle. But what is the proof? 2 -2 5

Compute shortest distances in the residual network 7 Let d(j) be the shortest path

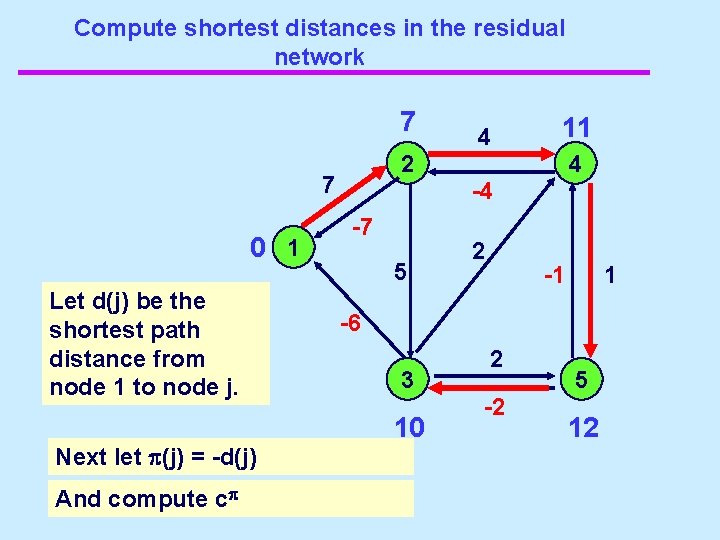
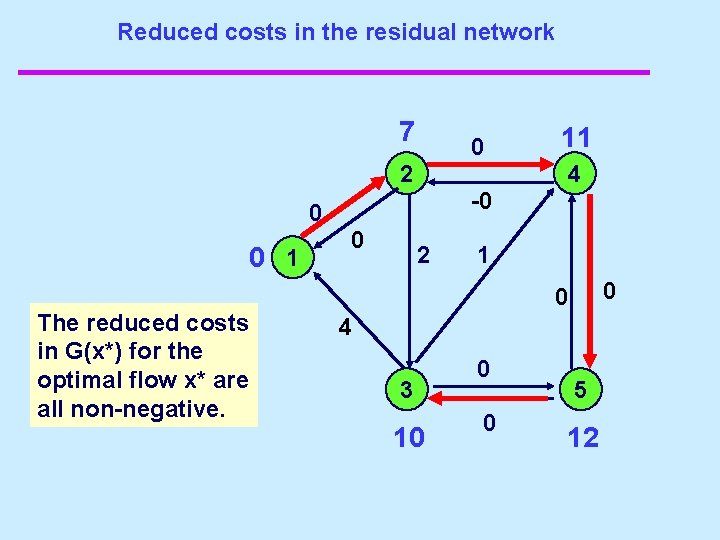
Compute shortest distances in the residual network 7 Let d(j) be the shortest path distance from node 1 to node j. Next let p(j) = -d(j) And compute cp 11 2 7 0 1 4 4 -4 -7 5 2 -1 1 -6 3 10 2 -2 5 12

Reduced costs in the residual network 7 0 2 4 -0 0 0 1

Reduced costs in the residual network 7 0 2 4 -0 0 0 1 The reduced costs in G(x*) for the optimal flow x* are all non-negative. 11 0 2 1 0 0 4 3 10 0 0 5 12

Assignments Reading 9. 1 --9. 6 Exercises 9. 16(a)(b) 9. 18

Assignments Reading 9. 1 --9. 6 Exercises 9. 16(a)(b) 9. 18