Lecture 13 Graphs Introduction to Graphs l Examples

Lecture 13 Graphs

Introduction to Graphs l Examples of Graphs – Airline Route Map l l – What is the fastest way to get from Pittsburgh to St Louis? What is the cheapest way to get from Pittsburgh to St Louis? Electric Circuits l l Circuit elements - transistors, resistors, capacitors is everything connected together? – Depends on interconnections (wires) l If this circuit is built will it work? – Depends on wires and objects they connect. – Job Scheduling l l l Interconnections indicate which jobs to be performed before others When should each task be performed All these questions can be answered using a mathematical object named a “graph” – – what are graphs? what are their basic properties?

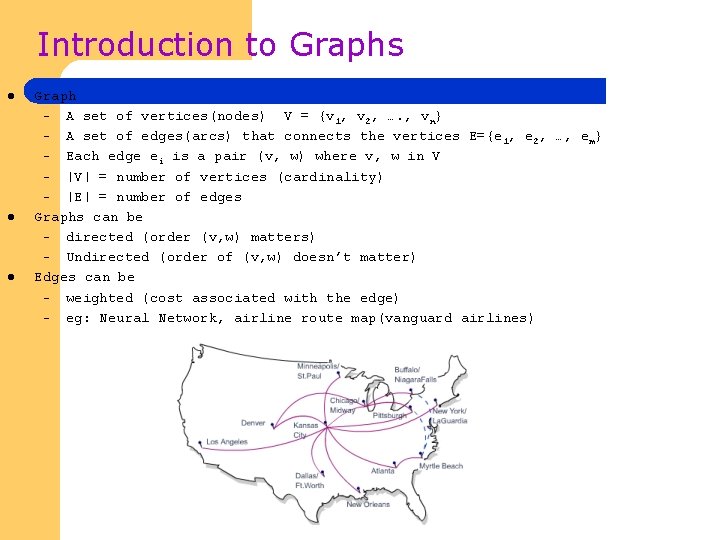
Introduction to Graphs l l l Graph – A set of vertices(nodes) V = {v 1, v 2, …. , vn} – A set of edges(arcs) that connects the vertices E={e 1, e 2, …, em} – Each edge ei is a pair (v, w) where v, w in V – |V| = number of vertices (cardinality) – |E| = number of edges Graphs can be – directed (order (v, w) matters) – Undirected (order of (v, w) doesn’t matter) Edges can be – weighted (cost associated with the edge) – eg: Neural Network, airline route map(vanguard airlines)

Paths and Graphs – – – A path is a sequence of edges from one node to another A length of a path is the number of edges l If w 1, w 2, …, wn is a sequence of vertices such that (wi, wi+1) in E, then there is a path of length n-1 from w 1 to wn. l what are paths of length 2 in vanguard airlines map? A simple path is a path where no vertex is repeated l first and last vertices can be the same l what is an example of a simple path in the vanguard map? l What is an example of a non-simple path? A cycle (in a directed graph) is a path that begins and ends in the same vertex. i. e. S = {w 1, w 2, …, wn} is a sequence such that w 1 = wn and |S| >1 A directed acyclic graph (DAG) is a directed graph having no cycles.

More Graph Definitions l Connected Graph – – – l Complete Graph – l A graph with all nodes connected to each other directly Maximal Edge count – – l A undirected graph is connected if for all (u, v) in V, there exists a path from u to v. A directed graph is strongly connected if for all (u, v) in V, there exists a path from u to v. A directed graph is weakly connected if for all (u, v) in V, either (u, v) is in E or (v, u) is in E. undirected graph |E|max = (n-1) + (n-2) + … + 2 + 1 = n(n 1)/2 directed graph |E|max = n(n-1) Degree – – number of edges incident to a vertex in a directed graph l l in-degree(sink) - number of edges into vertex out-degree(source) - number of edges from vertex

Some Cardinality Relations l l For most graphs |E| |V|2 A dense graph when most edges are present – – l E = (|V|2) A dense graph large number of edges (quadratic) Also |E| > |V| log |V| can be considered dense A sparse graph is a graph with relatively few edges – – – no clear definition metric for sparsity |E| < |V| log |V| eg: ring computer network

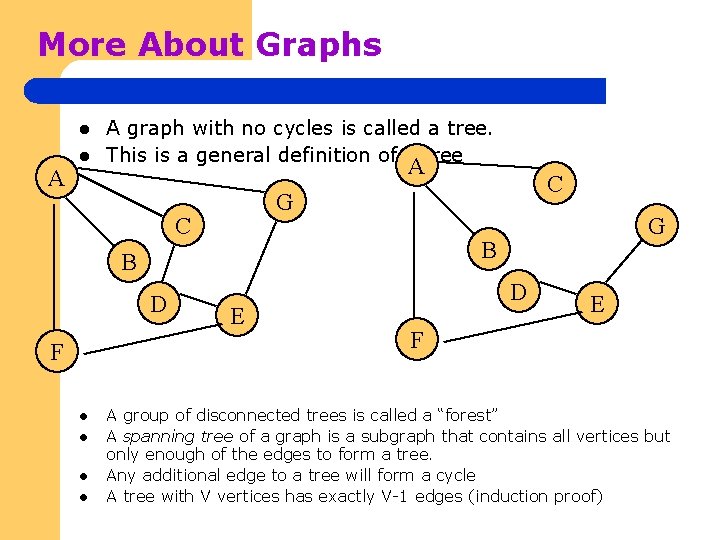
More About Graphs l A graph with no cycles is called a tree. This is a general definition of a tree A G C F l l G B B D C E D E F A group of disconnected trees is called a “forest” A spanning tree of a graph is a subgraph that contains all vertices but only enough of the edges to form a tree. Any additional edge to a tree will form a cycle A tree with V vertices has exactly V-1 edges (induction proof)

Graph Algorithms l Graphs depend on two parameters – – l edges (E) Vertices (V) Graph algorithms can be complicated to analyze – One algorithm might be order (V 2) l – Another might be order((E+V)log E) l l for dense graphs for sparse graphs Depth First Search – – – Is the graph connected? If not what are their connected components? Does the graph have a cycle? How do we examine (visit) every node and every edge systematically? First select a vertex, set all vertices connected to that vertex to nonzero Find a vertex that has not been visited and repeat the step above Repeat above until all zero vertices are examined.