Lecture 13 Dynamic Programming Steps The seven steps

Lecture 13

Dynamic Programming: Steps • The seven steps in the development of a dynamic programming algorithm are as follows: 1. Establish a recursive property that gives the solution to an instance of the problem. Develop a recursive algorithm as per recursive property See if same instance of the problem is being solved again an again in recursive calls Develop a memoized recursive algorithm See the pattern in storing the data in the memory Convert the memoized recursive algorithm into iterative algorithm Optimize the iterative algorithm by using the storage as required (storage optimization) 2. 3. 4. 5. 6. 7.

Exercise 1 • Initialise a two dimensional array A[1. . n, 1. . n] using following definition with an efficient algorithm. • A[i, j] = i + j if i = j • A[i, j] = Min(A[i, j-1], A[i+1, j])+ (i+j) if i < j • A[i, j] = Max(A[i-1, j], A[i, j+1])+ (i *j) if i > j • Where i is for row index and j is for column index.

Quiz Develop a recursive algorithm for the following definition, where P[] is a onedimensional array having indices from i-1 to j, and m is a two-dimensional array of size ixj

Solution for the Quiz • • • RMC(p, i, j) { if i = j return 0 m[i, j] = for(k = i; k <= j-1; k++) { q = RMC(p, i, k) + RMC(p, k+1, j) + pi-1 pkpj if(q < m[i, j]) m[i, j] = q } return m[i, j]; }

Quiz Convert the algorithm of the previous Quiz into an iterative algorithm

Quiz Develop a recursive algorithm for the following definition, C(i, j) = 0 c(i-1, j-1) + 1 max (c(i, j-1), c(i-1, j)) if i = 0 or j = 0 if i, j > 0 and xi = yj if i, j > 0 and xi yj X = <x 1, x 2, x 3, …. . , xm> Y = <y 1, y 2, y 3, …. . , yn> i varies from m to 0 and j varies from n to 0

Quiz • Develop a memoized recursive algorithm for the following definition C(i, j) = 0 c(i-1, j-1) + 1 max (c(i, j-1), c(i-1, j)) if i = 0 or j = 0 if i, j > 0 and xi = yj if i, j > 0 and xi yj X = <x 1, x 2, x 3, …. . , xm> Y = <y 1, y 2, y 3, …. . , yn> i varies from m to 0 and j varies from n to 0

Quiz Convert the algorithm of the previous Quiz into an iterative algorithm

Third Practice Problem – Quiz Develop a recursive and memoized recursive algorithm for the following recursive definition P is an array of j elements A[i, i] = Pi A[i, i-1] and A[j+1, j] are defined to be 0

Home Exercise • Convert the iterative algorithm of the quizzes into one which consume memory as per requirement of the problem

Matrix Multiplications • We can multiply two matrices A and B if Columns of A = Rows of B I. e. order of A = p * q and order of B = q * r void Matrix_Multiply(A, B) { If (columns of A != Rows of B) error else {for(I = 1; I <= n; I++) for(j = 1; j <= N; j++) {C[ I ][ j ] = 0; for(k = 1; k <= N; k++) C[ I ][ j ] += A[ I ][k ] * B[ k ][ j ] } } } No. of Scalar Multiplications = p * q * r

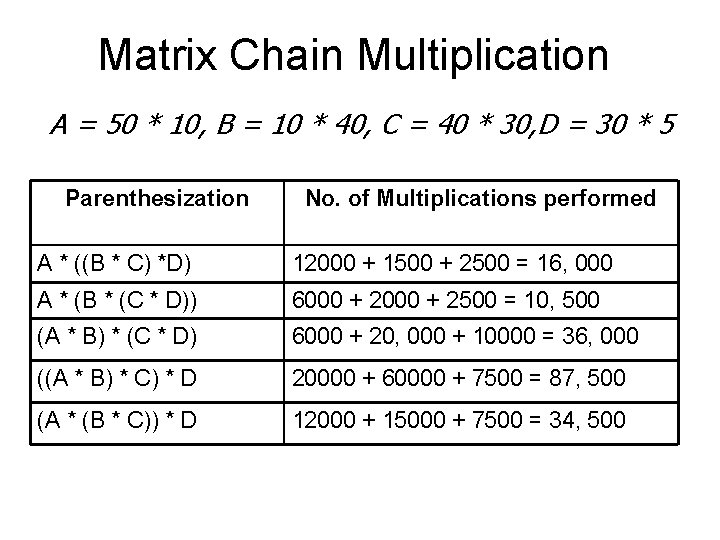
Matrix Chain Multiplication • Problem arises when we want to multiply a chain of matrices. For example A = 50 * 10 B = 10 * 40 C = 40 * 30 D = 30 * 5 • We want to compute A * B * C * D. • In which sequence should we call matrix multiply? • Matrix multiplication is associative.

Matrix Chain Multiplication A = 50 * 10, B = 10 * 40, C = 40 * 30, D = 30 * 5 Parenthesization No. of Multiplications performed A * ((B * C) *D) 12000 + 1500 + 2500 = 16, 000 A * (B * (C * D)) 6000 + 2500 = 10, 500 (A * B) * (C * D) 6000 + 20, 000 + 10000 = 36, 000 ((A * B) * C) * D 20000 + 60000 + 7500 = 87, 500 (A * (B * C)) * D 12000 + 15000 + 7500 = 34, 500

Matrix Chain Multiplication Problem • Given a chain <A 1, A 2, …. , An> of n matrices. • Multiply all the matrices with minimum cost • First Compute the order in which matrices should be multiplied • Or in other words • We have to find an optimum sequence or an optimum parenthesization of matrix chain multiplication. • Then by using that order multiply the matrices.

Matrix Chain Multiplication Problem Bottom Up Approach with Memoization Matrix-Chain-Multiply(A [ ] , s[ ], i, j) // A is an array of matrices // s is an array of order, s[i, j] represents parenthesization position for // matrix i to j { if (j > i){ X = Matrix-Chain-Multiply(A, s, i, s[i, j]); Y = Matrix-Chain-Multiply(A, s, s[i, j]+1, j); return Matrix-Multiply(X, Y); } else return Ai } The problem is to compute s[i, j] for a given chain of matrices from i to j.

Formulation of the problem • Fully parenthesize the product A 1 * A 2…. An in a way that minimizes the number of scalar multiplications.

Matrix Chain Multiplication Problem • • • Ai. . j is a notation for the matrix that results from evaluating the product Ai. Ai+1…Aj. An optimal parenthesization of the product A 1 A 2…. An splits the product between Ak and Ak+1 for some integer k in the range 1<=k<n For some value of k we first Compute the matrices A 1. . k and Ak+1. . n and then Multiply them together to produce the final product A 1. . n.

Matrix Chain Multiplication Problem • The cost of this optimal parenthesization is thus the – Cost of computing the matrix A 1. . k, plus – The cost of computing Ak+1. . n, plus – The cost of multiplying them together.

Matrix Chain Multiplication Problem • • Parenthesization of the “prefix” sub chain A 1 A 2…Ak within this optimal parenthesization of A 1 A 2…An must be – An optimal parenthesization of A 1 A 2…Ak. Why? A similar observation holds for the parenthesization of the sub chain Ak+1 Ak+2…An Thus, an optimal solution to an instance of the matrix-chain multiplication problem contains within it optimal solutions to sub problem instances.

Matrix Chain Multiplication Problem A Recursive Solution • • • Define the value of an optimal solution recursively in terms of the optimal solutions to subproblems. For this problem, we pick as our subproblems the problems of determining the minimum cost of a parenthesization of Ai. Ai+1…. Aj, for 1 <= i <= j <=n

A Recursive Solution • Let m[i, j] be the minimum number of scalar multiplications needed to compute the matrix Ai. . j; • The cost of cheapest way to compute A 1. . n would thus be m[1, n]

A Recursive Solution • • We can define m[i, j] recursively as follows: If i = j, the chain consists of just one matrix Ai. . i=Ai, so – No scalar multiplications are necessary to compute the product. Thus – m[i, i] = 0 for i = 1, 2, …. . , n. To compute m[i, j] when i < j, we take advantage of the structure of an optimal solution from step 1. Assume that optimal parenthesization splits the product Ai, Ai+1, …. Aj between Ak and Ak+1, where i<=k < j.

A Recursive Solution • Now m[i, j] is equal to the minimum cost for – Computing the subproducts A 1. . k, and – Computing the subproducts Ak+1. . j, plus – The cost of multiplying these two matrices together. • For i = 1, 2, …. . , n, matrix Ai has dimensions Pi-1*Pi • Since computing the matrix product A 1. . k. Ak+1. . j takes pi-1 pkpj scalar multiplications, we obtain • m[i, j] = m[i, k] + m[k+1, j] + pi-1 pkpj • But we don’t know the value of k for an optimum solution. • There are only j-1 possible values for k, namely k=i, i+1, …j-1.

A Recursive Solution • Since, the optimal parenthesization must use one of these values for k, we need only check them all to find the best. • Thus, our recursive definition for the minimum cost of parenthesizing the product Ai, Ai+1, … Aj becomes

Matrix Chain Multiplication Problem • Based on this recurrence, we can easily write the recursive algorithm to compute the minimum cost m[1. . n] for multiplying A 1, A 2, …. , An. Recursive-Matrix-Chain(p, i, j) { 1. if i = j 2. return 0 3. Min. Cost = 4. for(k = i; k <= j-1; k++) { q = Recursive-Matrix-Chain(p, i, k) + Recursive-Matrix. Chain(p, k+1, j) + pi-1 pkpj if(q < Min. Cost) 5. Min. Cost = q 6. } 8. return Min. Cost; }

Matrix Chain Multiplication Problem • • A recursive algorithm may encounter each sub problem many times in different branches of its recursion tree. Instead of computing the same solution again and again, we can use the memoization strategy.

Matrix Chain Multiplication Problem Top Down Recursive Approach with Memoization Memoized-Matrix-Chain(p) { n = length[p] – 1; for(i= 1; i <= n; i++) for(j = i; j <= n; j++) m[i, j] = return Look. Up-Chain(p, 1, n); }

Matrix Chain Multiplication Problem Top Down Recursive Approach with Memoization Look. Up-Chain(p, i, j) { if( m[i, j] < ) return m[i, j] if(i == j) m[i, j] = 0; else { for(k = i; k <= j-1; k++) { q = Look. Up-Chain(p, I, k) + Look. Up-Chain(p, k+1, j) + pi-1 pkpj if(q < m[i, j]) { m[i, j] = q; s[i, j] = k; } } }

Matrix Chain Multiplication Problem Bottom Up Heuristic Approach To keep track of how to construct an optimal solution, let us define – s[i, j] to be a value of k at which we can split the product Ai, Ai+1, … Aj to obtain an optimal parenthesization. i. e. – s[i, j] equals a value k such that m[i, j] = m[i, k] + m[k+1, j] + p i 1 pkpj.

Matrix Chain Multiplication Problem Bottom Up Approach with Memoization Matrix-Chain-Order(p) 1. { n = length(p) – 1 2. for(i = 1; i <= n; i++) 3. for(l = 2; l <= n; l ++) m[i, i] = 0; 4. for(i = l; i<=n-l+1; i++) 5. { j = i + l – 1; m[i, j] = 6. for(k = i; k<= j-1; k++) 7. { q = m[i, k] + m[k+1, j] + pi-1 pkpj 8. if (q < m[i, j]) 9. { 10. 11. 12. 13. 14. } m[i, j] = q; s[i, j] = k; } } } return m and s;

Matrix Chain Multiplication Problem Bottom Up Approach with Memoization Matrix-Chain-Multiply(A , s, i, j) { if (j > i) { X = Matrix-Chain-Multiply(A, s, i, s[i, j]); Y = Matrix-Chain-Multiply(A, s, s[i, j]+1, j); return Matrix-Multiply(X, Y); } else return Ai }

Next Lecture

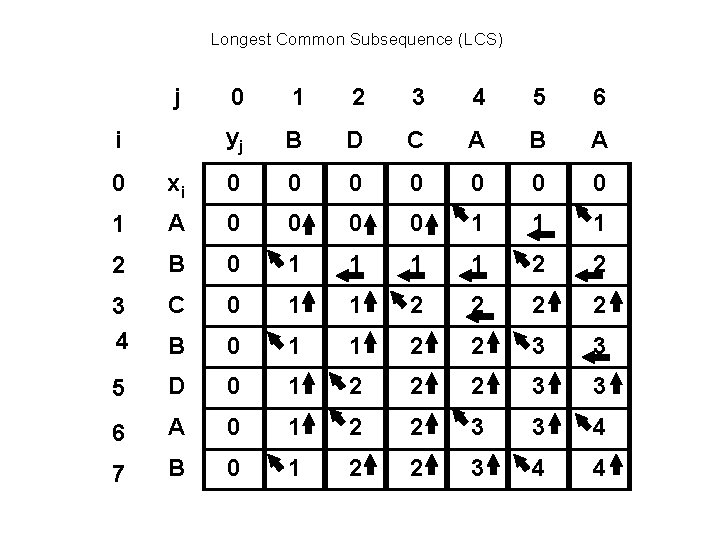
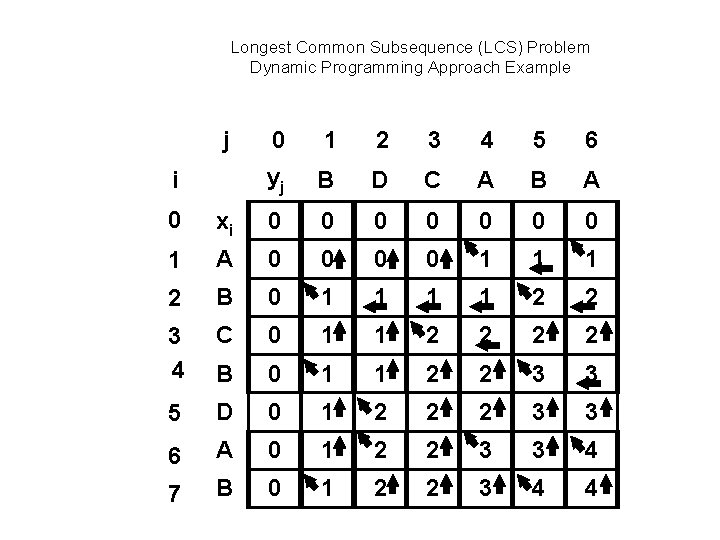
Longest Common Subsequence (LCS) Problem • Given two sequences of symbols, X and Y, determine the longest subsequence of symbols that appears in both X and Y. • Example: X = <A, B, C, B, D, A, B> Y = <B, D, C, A, B, A> • LCS of X, Y? <B, C, B, A> <B, D, A, B>

Longest Common Subsequence (LCS) Problem Brute Force Approach 1. Enumerate all subsequences of X. 2. Each subsequence of X corresponds to a subset of indices {1, 2, …. , m} of X. 3. There are 2 m subsequences of X, so this approach requires exponential time.

Longest Common Subsequence (LCS) j 0 1 2 3 4 5 6 i yj B D C A B A 0 xi 0 0 0 0 1 A 0 0 1 1 1 2 B 0 1 1 2 2 3 4 C 0 1 1 2 2 B 0 1 1 2 2 3 3 5 D 0 1 2 2 2 3 3 6 A 0 1 2 2 3 3 4 7 B 0 1 2 2 3 4 4

l l l LCS – Algorithm: Constructing an LCS Table b[1. . m, 1. . n] can be used to construct an LCS. Initial invocation is Print_LCS(b, X, length[X], length[Y]). Print_LCS(b[], X[], i, j) { if(i = = 0 or j = = 0) return 0; if(b[i, j] = = “ ” // common elements { Print_LCS(b, X, I-1, j-1); print xi; } else if (b[I, j] = = “ ”) Print_LCS(b, X, I-1, j); else Print_LCS(b, X, I, j-1); } l Devise a memoized version of LCS_Length();

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach I. Characterize the LCS problem • The LCS problem has an optimal substructure property. • Can we formulate optimal substructure? • ith preifx of a sequence X is Xi, e. g. , • X 4 of sequence X = <A, B, C, B, D, A, B> is <A, B, C, B>

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach Optimal Substructure of an LCS: Let X = <x 1, x 2, x 3, …. . , xm> and Y = <y 1, y 2, y 3, …. . , yn> and let Z = <z 1, z 2, z 3, …. zk> be any LCS of X and Y 1. If xm = yn then zk = xm = yn and zk-1 is an LCS of Xm-1 and Yn-1. 2. If xm yn then zk xm implies that Z is an LCS of Xm-1 and Y. 3. If xm yn then zk yn implies that Z is an LCS of X and Yn-1

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach Step 1: Characterizing an LCS • LCS problem has an optimal substructure property. I. e. • There are either one or two subproblems to examine when finding an LCS of X = <x 1, x 2, …. . , xm>, Y = <y 1, y 2, …. . , yn> • if xm = yn – If xm yn • • find an LCS of Xm-1 and Yn-1 appending xm and yn (xm = yn) to this LCS yields an LCS of X and Y. – solve two subproblems: I. Finding an LCS of Xm-1 and Y II. Finding an LCS of X and Yn-1 – Longer of I and II is an LCS of X and Y. This shows overlapping subproblmes property in LCS.

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach Step II: Define a recursive solution • Establish a recurrence for the cost of an optimal solution. • Let c[i, j] to be the length of the longest subsequences (LCS) of Xi and Yj. c[i, j] = 0 if i = 0 or j = 0 c[i-1, j-1] + 1 if i, j > 0 and xi = yj max(c[i, j-1], c[i-1, j]) if i, j > 0 and xi yj ¨ Write a recursive algorithm to compute the length of an LCS of two sequences?

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach Step III: Devise an algorithm to compute the length of an LCS and then construct the LCS. • Development of an algorithm • Input two sequences X and Y and a two dimensional table c[0. . m, 0. . n] • According to the definition for(i = 1; I <= m; I++) { for(j = 1; j <= n; j++) { if (X[i] = = Y[j]) c[i, j] = c[i-1, j-1] + 1 else if (c[i-1, j] >= c[i, j-1]) else } } /* It means to compute c[i, j] = c[i-1, j]; We need to know c[i, j] = c[i, j-1]; c[i-1, j-1], c[i, j-1] and c[i-1, j] */

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach Example j 0 1 2 3 4 5 6 i yj B D C A B A 0 xi 0 0 0 0 1 A 0 0 1 1 1 2 B 0 1 1 2 2 3 4 C 0 1 1 2 2 B 0 1 1 2 2 3 3 5 D 0 1 2 2 2 3 3 6 A 0 1 2 2 3 3 4 7 B 0 1 2 2 3 4 4

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach Example • LCS – Algorithm: Computing the length LCS-Length(X, Y) { m = length[X]; n = length[Y]; for(i = 1; i <= m; i++) c[i, 0] = 0; for(j = 0; j <= n; j++) c[0, j] = 0; for(i = 1; i <= m; I++) { for(j = 1; j <= n; j++) { if(X[i] = = Y[i] { c[i, j] = c[i-1, j-1] + 1; b[I, j] = “ ” else if(c[i-1, j] >= c[i, j-1]) { c[i, j] = c[i-1, j]; b[I, j] = “ ” else { c[i, j] = c[i, j-1]; b[I, j] = “ ” } } return c and b; } Complexity: O(m*n) } } }

Longest Common Subsequence (LCS) Problem Dynamic Programming Approach Example • LCS – Algorithm: Constructing an LCS • Table b[1. . m, 1. . n] returned by LCS-length() can be used to construct an LCS. • Initial invocation is Print_LCS(b, X, length[X], length[Y]). Print_LCS(b, X, i, j) { if(i = = 0 or j = = 0) return 0; if(b[i, j] = = “ ” { Print_LCS(b, X, I-1, j-1); print xi; } else if (b[I, j] = = “ ”) Print_LCS(b, X, I-1, j); else Print_LCS(b, X, I, j-1); } • Devise a memoized version of LCS_Length();