Lecture 13 Cox PHM Part II Basic Cox

Lecture 13: Cox PHM Part II Basic Cox Model Parameter Estimation Hypothesis Testing

Recall Basic Cox PHM • Model • Linear form • Proportional hazards because

Likelihood • Full likelihood • Log-likelihood

Partial Likelihood • The partial likelihood is defined as • Where – j = 1, 2, …, n – No ties – t 1 < t 2 < … < t. D – Z(i)k is the kth covariate associated with the individual whose failure time is ti – R(ti) is the risk set at time ti

Estimation • We can use the log of the likelihood to obtain and MLE for b • Maximize log-likelihood to solve for estimates of b • Score equations and information matrices are found using standard approaches • Solving for estimates can be done numerically (e. g. Newton-Raphson)

Tests of the Model • Testing that bk = 0 for all k = 1, 2, …, p • Three main tests – Chi-square/ Wald test – Likelihood ratio test – Score test • All three have chi-square distribution with p degrees of freedom

Score Equations an Information Matrix • MLE found by Uh(b) = 0 using Newton-Raphson (need Uh(b) and I(b)). • Start with an initial guess for b • After ith step of the algorithm the updated guess is • Repeat this process until convergence achieved

Developing the Tests • In order to develop the tests, we must be able to define – Log-likelihood for the partial likelihood expression – The score equation(s) Uh(b) – The information matrix I(b) • A simple example… – 3 observed times: ti = t 1 < t 2 < t 3 – Event indicators: di = 1, 1, 0 – 1 covariate: zi = z 1, z 2, z 3

Log-likelihood

Score Equation

Information (Matrix)

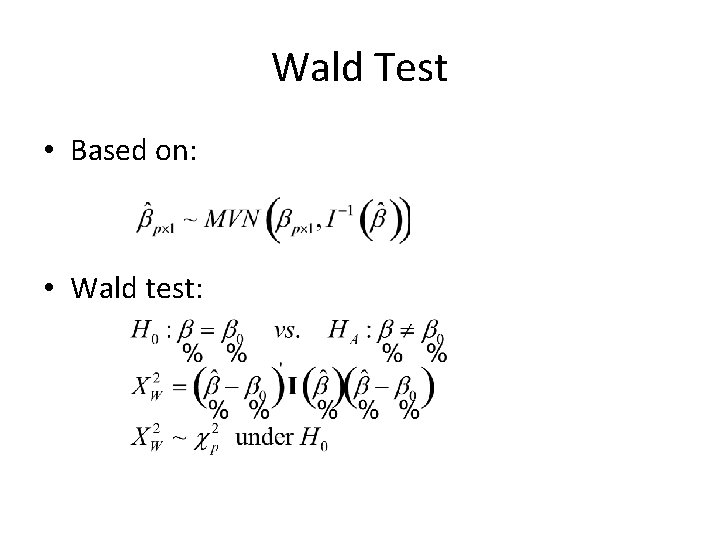
Wald Test • Based on: • Wald test:

Score Test • Based on: • Score test:

Likelihood Ratio Test

Partial Likelihood for Ties? • The previous partial likelihood only applies when there are no ties • Three primary approaches – Breslow – Efron – Cox • When ties are few, all three perform similarly

Breslow (1974) • si is the sum of the vectors Zj over all individuals who die at time ti • Consider each of the di events at a given time as distinct

Efron (1977) • Di is the set of individuals who have the event at time ti • Closer to the correct partial likelihood score based on a discrete hazard model than Breslow’s

Cox (1972) • Based on discrete time, hazard-rate model • Assumes logistic model for hazard rate – Let h(t | Z) be the conditional event probability in (t, t + 1) given survival to time t – Assume

Cox (1972)- Discrete • This is the “proper” partial likelihood • Where – Qi = a di – tuple of individuals who could have been one of the di failures at ti – q = {q 1, q 2, …, qdi } is one of the elements of Qi –.

Why Not Use Cox Every Time? • Consider the computation • Denominator of Cox partial likelihood is more complicated • Efron and Breslow approaches are less intensive to calculate • R can do all three

“Local” Tests • Testing individual coefficients • But, more interestingly, testing a set of coefficients • Examples – Testing treatment variables (3 categories) – Testing extent spread (4 categories) • Same as previous – Wald test – Score test – Likelihood ratio test

Wald test •

Wald test • The Wald test is then • Where I 11(b) is the upper qxq submatrix of I(b) • This statistics is distributed ~c 2 with q degrees of freedom

Score Test • Define • This is the vector of q scores for • The score test is then , evaluated at • This statistics is distributed ~c 2 with q degrees of freedom

Likelihood Ratio Test • Define b 2(b 10) be the partial maximum likelihood estimates of b 2 based on the model with b 1 set to b 10 • The LRT is • Where LL = log-likelihood • LRT has ~ chi-square distribution with p degrees of freedom under H 0

Example • Study examining impact of cancer stage and age at diagnosis on survival in men with larynx cancer. • 90 subjects • Outcome = time to death from diagnosis • Variables – Age at diagnosis – Stage (I-IV)

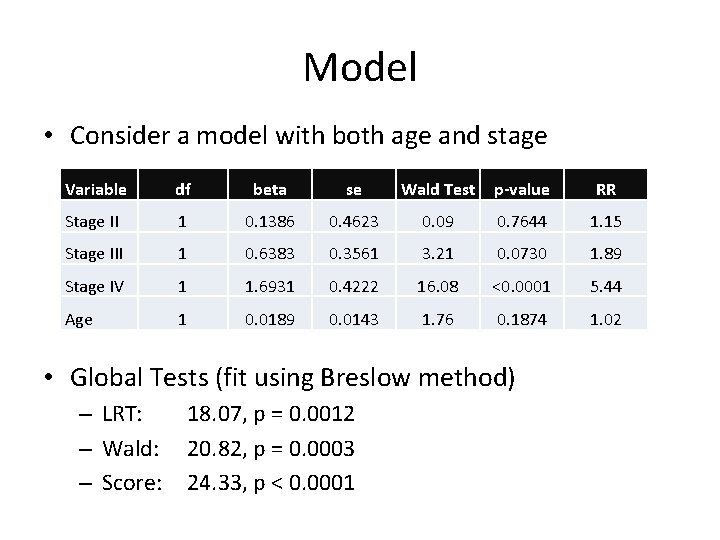
Model • Consider a model with both age and stage Variable df beta se Wald Test p-value RR Stage II 1 0. 1386 0. 4623 0. 09 0. 7644 1. 15 Stage III 1 0. 6383 0. 3561 3. 21 0. 0730 1. 89 Stage IV 1 1. 6931 0. 4222 16. 08 <0. 0001 5. 44 Age 1 0. 0189 0. 0143 1. 76 0. 1874 1. 02 • Global Tests (fit using Breslow method) – LRT: – Wald: – Score: 18. 07, p = 0. 0012 20. 82, p = 0. 0003 24. 33, p < 0. 0001

Local Test • Say we want to test whether or not the beta’s for stage are all 0… • H 0 : • Necessary info depends on the test we want to use – LRT: need log(L(b)) for “full” and “null” models – Wald: need b 1 and I 11 – Score: need U 1[b 10, b 2(b 10)] and I 11(b 10, b 2(b 10))

Local Test: LRT • Null Model: • Full Model: • log(L(b)) for full model: -188. 18 • log(L(b)) for null model: -195. 91

Local Test: Wald Test • Information Matrix: • Test:

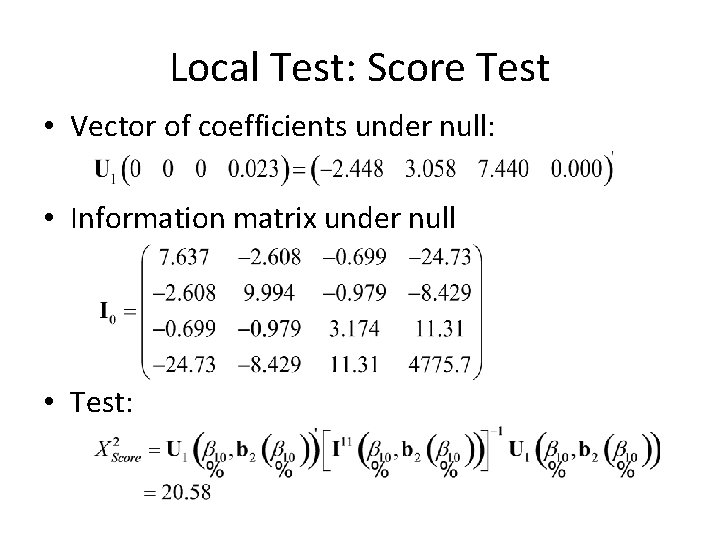
Local Test: Score Test • Vector of coefficients under null: • Information matrix under null • Test:

Contrasts • Recall test for H 0: c’b = c’b 0 • When a covariate is a factor (e. g. stage), we can test contrasts – Stage II vs. Stage III – Stage II vs. Stage IV – Stage III vs. Stage IV • Define scalar contrast matrix, c, and test H 0: c’b = 0

Fitting Models In R • coxph function for fitting CPHMs – Coefficient estimates – Global tests (LRT, Wald, and Score) – Local test for each individual covariate • We can also easily conduct local tests ant contrasts using – LRT – Wald • Score not so easy…

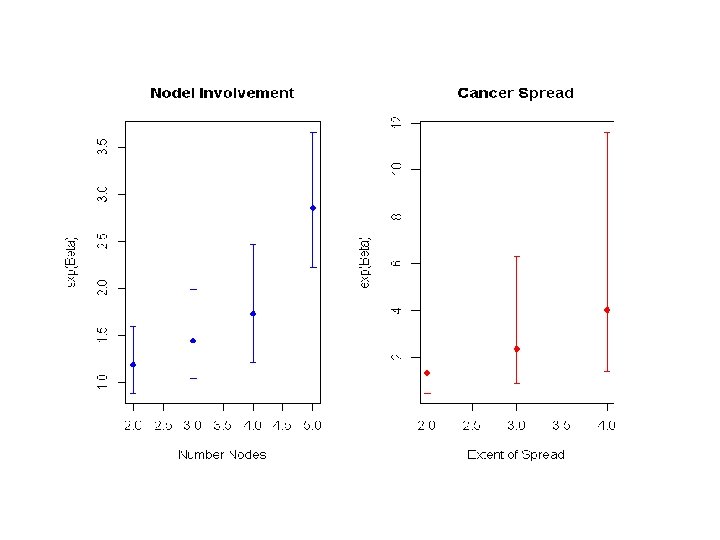
Example: Colon Cancer • Trial of adjuvant chemotherapy for colon cancer. • 929 subject – Main variable of interest is treatment • Placebo • Levamisiole • Levamisole + 5 -FU – Other variables • • • Demographics (gender, age) Tumor obstruction (yes/no) Number of lymph nodes involved (number with detectable cancer) Extent of local spread (submucosa, muscle, serosa, more) Adherence to other organs (yes/no) • Outcome: Time to cancer recurrence

Some of the Covariates

Fitting in R • Treating factors as ordinal reg 2<-coxph(st~sex+rx+perfor+obstruct+adhere+nodes 2+ extent, data=coln) • Treating factors as nominal reg 3<coxph(st~sex+rx+perfor+obstruct+adhere+factor(nodes 2)+ factor(extent), data=coln)

Cox PHM Approach > data(colon) > coln<-colon[2*(1: 929), ] > st<-Surv(coln$time, coln$status) > reg 1<-coxph(st~coln$rx) > attributes(reg 1) $names [1] "coefficients" "var" "loglik" "score" "iter" "linear. predictors" [7] "residuals" "means" "concordance" "method" "nevent" [13] "terms" "assign" "wald. test" "y" "formula" "xlevels" [19] "contrasts" "call" $class [1] "coxph" > reg 1$coef coln$rx. Lev+5 FU -0. 01512329 -0. 51209312

Results > summary(reg 1) Call: coxph(formula = st ~ coln$rx) n= 929, number of events= 468 coef exp(coef) se(coef) z Pr(>|z|) coln$rx. Lev -0. 01512 0. 98499 0. 10708 -0. 141 0. 888 coln$rx. Lev+5 FU -0. 51209 0. 59924 0. 11863 -4. 317 1. 58 e-05 *** --Signif. codes: 0 ‘***’ 0. 001 ‘**’ 0. 01 ‘*’ 0. 05 ‘. ’ 0. 1 ‘ ’ 1 exp(coef) coln$rx. Lev 0. 9850 coln$rx. Lev+5 FU 0. 5992 exp(-coef) lower. 95 1. 015 0. 7985 1. 669 0. 4749 Likelihood ratio test = 24. 34 on 2 df, p=5. 175 e-06 Wald test = 22. 58 on 2 df, p=1. 247 e-05 Score (logrank) test = 23. 07 on 2 df, p=9. 804 e-06 upper. 95 1. 2150 0. 7561

Multiple Regression Results > summary(reg 2) Call: coxph(formula = st ~ sex + rx + perfor + obstruct + adhere + nodes 2 + extent, data = coln) n= 911, number of events= 456 (18 observations deleted due to missingness) coef exp(coef) sex -0. 12256 0. 88465 0. 09410 rx. Lev -0. 04272 0. 95818 0. 10833 rx. Lev+5 FU -0. 52460 0. 59179 0. 12077 perfor 0. 07865 1. 08182 0. 25567 obstruct 0. 14509 1. 15614 0. 11649 adhere 0. 25080 1. 28505 0. 12656 nodes 2 0. 26254 1. 30023 0. 02995 extent 0. 53403 1. 70579 0. 11632 --Likelihood ratio test= 140. 7 on 8 df, p=0 Wald test = 134. 3 on 8 df, p=0 Score (logrank) test = 139. 1 on 8 df, p=0 z -1. 303 -0. 394 -4. 344 0. 308 1. 245 1. 982 8. 765 4. 591 Pr(>|z|) 0. 1927 0. 6933 1. 40 e-05 *** 0. 7584 0. 2130 0. 0475 * < 2 e-16 *** 4. 41 e-06 ***

Multiple Regression Results > summary(reg 3) Call: coxph(formula = st ~ sex + rx + perfor + obstruct + adhere + factor(nodes 2) + factor(extent), data = coln) sex rx. Lev+5 FU perfor obstruct adhere factor(nodes 2)2 factor(nodes 2)3 factor(nodes 2)4 factor(nodes 2)5 factor(extent)2 factor(extent)3 factor(extent)4 coef -0. 11420 -0. 04064 -0. 52281 0. 12790 0. 16688 0. 23380 0. 17549 0. 36671 0. 54757 1. 04969 0. 28810 0. 84962 1. 39427 exp(coef) 0. 89208 0. 96017 0. 59285 1. 13643 1. 18162 1. 26339 1. 19183 1. 44299 1. 72904 2. 85676 1. 33389 2. 33876 4. 03201 se(coef) 0. 09475 0. 10890 0. 12106 0. 25665 0. 11726 0. 12818 0. 15009 0. 16319 0. 18054 0. 12654 0. 53106 0. 50643 0. 53974 z -1. 205 -0. 373 -4. 319 0. 498 1. 423 1. 824 1. 169 2. 247 3. 033 8. 295 0. 543 1. 678 2. 583 Pr(>|z|) 0. 22810 0. 70899 1. 57 e-05 *** 0. 61826 0. 15468 0. 06816. 0. 24229 0. 02463 * 0. 00242 ** < 2 e-16 *** 0. 58747 0. 09341. 0. 00979 **

Ties? > table(duplicated(st)) FALSE TRUE 751 1107 > coxph(st~rx, data=coln) coef exp(coef) se(coef) rx. Lev -0. 0151 0. 985 0. 107 rx. Lev+5 FU -0. 5121 0. 599 0. 119 z -0. 141 -4. 317 p 8. 9 e-01 1. 6 e-05 Likelihood ratio test=24. 3 on 2 df, p=5. 17 e-06 n= 929, number of events= 468 > coxph(st~rx, data=coln, ties="breslow") coef exp(coef) se(coef) rx. Lev -0. 0152 0. 985 0. 107 rx. Lev+5 FU -0. 5119 0. 599 0. 119 z -0. 142 -4. 315 p 8. 9 e-01 1. 6 e-05 Likelihood ratio test=24. 3 on 2 df, p=5. 23 e-06 n= 929, number of events= 468 > coxph(st~rx, data=coln, ties="exact") coef exp(coef) se(coef) rx. Lev -0. 0152 0. 985 0. 107 rx. Lev+5 FU -0. 5122 0. 599 0. 119 z -0. 142 -4. 317 p 8. 9 e-01 1. 6 e-05 Likelihood ratio test=24. 3 on 2 df, p=5. 19 e-06 n= 929, number of events= 468

Run Time > system. time(coxph(st~rx, data=coln)) user system elapsed 0 0 0 > system. time(coxph(st~rx, data=coln, ties="breslow")) user system elapsed 0 0 0 > system. time(coxph(st~rx, data=coln, ties="exact")) user system elapsed 0. 01 0. 00 0. 02

Local Tests • Say we wanted to determine if extent of local spread mattered in the model • Four categories: – 1 = submucosa – 2 = muscle – 3 = serosa – 4 = contiguous structures • We can use our local tests here (must set it up ourselves in R) – LRT – Wald

Local Test: LRT > full_fit<-coxph(st ~ sex + rx + perfor + obstruct + adhere + factor(nodes 2)+ factor(extent), data=coln) > LLfull<-full_fit$loglik[2] > LLfull [1] -2883. 81 > null_fit<-coxph(st ~ sex + rx + perfor + obstruct + adhere + factor(nodes 2), data=coln) > LLnull<-null_fit$loglik[2] > LLnull [1] -2895. 227 > LRT_extent<-2*(LLfull-LLnull) > LRT_extent [1] 22. 83403 > pval<-pchisq(LRT_extent, df=3, lower=F) > pval [1] 4. 373093 e-05

Local Test: Wald Test > reg 3<-coxph(st~sex+rx+perfor+obstruct+adhere+factor(nodes 2)+ factor(extent), data=coln) > wald_extent<-t(reg 3$coeffic[11: 13])%*%solve(reg 3$var[11: 13, 11: 13])%*% reg 3$coeffic[11: 13] > wald_extent [, 1] [1, ] 21. 25669 > pval<-pchisq(wald_extent, df=3, lower=F) > pval [, 1] [1, ] 9. 311276 e-05

Contrasts • Since at least one of the extent of spread categories was not 0, we may also want to contrast the four categories • We can use contrasts but again, we must set this up ourselves in R.

Contrasts in R > E 2 v. E 3<-reg 3$coef[11: 12]%*%c(-1, 1) > se 2 v 3<-sqrt(reg 3$var[11, 11]+reg 3$var[12, 12]-2*reg 3$var[11, 12]) > z 2 v 3<-E 2 v. E 3/se 2 v 3 > z 2 v 3 [, 1] [1, ] 2. 730731 > 2*(1 -pnorm(abs(z 2 v 3))) [, 1] [1, ] 0. 001843819 > E 2 v. E 4<-reg 3$coef[c(11, 13)]%*%c(-1, 1) > se 2 v 4<-sqrt(reg 3$var[11, 11]+reg 3$var[13, 13]-2*reg 3$var[11, 13]) > z 2 v 4<-E 2 v. E 4/se 2 v 4 > z 2 v 4 [, 1] [1, ] 4. 286233 > 2*(1 -pnorm(abs(z 2 v 4))) [, 1] [1, ] 1. 817281 e-05

Confidence Interval • Construct a 95% CI for the hazard ratio between different extent of local spread categories • For specific model coefficient • For a contrast

CIs for Contrasts in R > ucv 23<-E 2 v. E 3+qnorm(. 975)*se 2 v 3 > lcv 23<-E 2 v. E 3 -qnorm(. 975)*se 2 v 3 > hr 23<-exp(E 2 v. E 3) > hr 23 [, 1] [1, ] 1. 753335 > uhr 23<-exp(ucv 23) > uhr 23 [, 1] [1, ] 2. 496546 > lhr 23<-exp(lcv 23) > lhr 23 [, 1] [1, ] 1. 231374

Confidence Interval • Conclusion: – Adjusting for other covariates in the model, the risk of death among individuals with serosa involvement is 1. 75 times the risk of death relative to subjects with only muscle involvement (95% CI for RR 1. 23 -2. 50).

Proportional? • Recall we are making a strong assumption that we have proportional hazards for each covariate • We can investigate this to some extent via graphical displays • BUT limited for quantitative variables • We’ll learn more about this later