Lecture 12 Range Queries and MultiDimensional Search Structures


![Finding all Elements in [a, b] in a Dictionary • First find a (or Finding all Elements in [a, b] in a Dictionary • First find a (or](https://slidetodoc.com/presentation_image_h/b6aad98a96c5b57096c7a65ba19cb714/image-4.jpg)













- Slides: 26

Lecture 12. Range Queries and Multi-Dimensional Search Structures Cp. Sc 212: Algorithms and Data Structures Brian C. Dean School of Computing Clemson University Fall, 2012

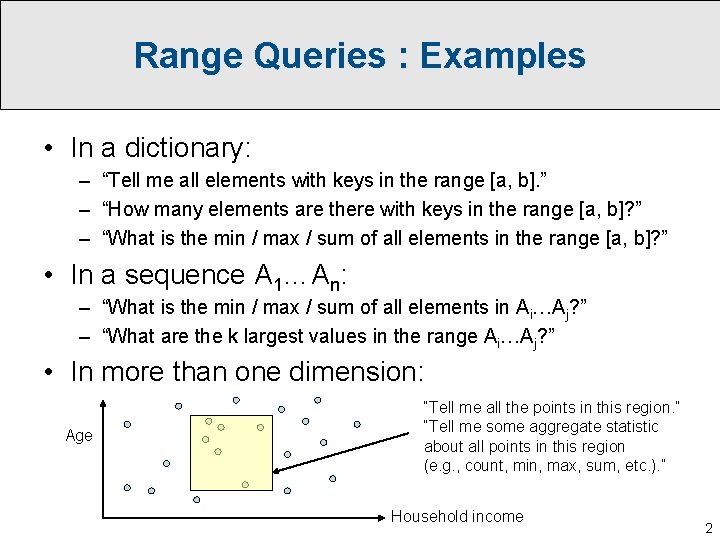
Range Queries : Examples • In a dictionary: – “Tell me all elements with keys in the range [a, b]. ” – “How many elements are there with keys in the range [a, b]? ” – “What is the min / max / sum of all elements in the range [a, b]? ” • In a sequence A 1…An: – “What is the min / max / sum of all elements in Ai…Aj? ” – “What are the k largest values in the range Ai…Aj? ” • In more than one dimension: Age “Tell me all the points in this region. ” “Tell me some aggregate statistic about all points in this region (e. g. , count, min, max, sum, etc. ). ” Household income 2

Range Updates : Examples • In a dictionary: – “Delete all elements in the range [a, b]. ” – “Apply some operation to all elements in the range [a, b]. ” • In a sequence A 1…An: – “Delete all elements in the range Ai…Aj. ” – “Increase all elements in Ai…Aj by a common value v. ” • In more than one dimension: Age “Apply some operation to all points in this region (e. g. , delete, change some attribute by a common value). ” Household income 3
![Finding all Elements in a b in a Dictionary First find a or Finding all Elements in [a, b] in a Dictionary • First find a (or](https://slidetodoc.com/presentation_image_h/b6aad98a96c5b57096c7a65ba19cb714/image-4.jpg)
Finding all Elements in [a, b] in a Dictionary • First find a (or the successor of a, if a is not present). • Then call successor repeatedly until we’ve stepped through all elements in [a, b]. LCA(a, b) = “lowest common ancestor” of a and b. a (or succ(a)) b (or pred(b)) = in the range [a, b]. • Total time: O(k + log n) on a balanced BST, where k is the number of elements written as output. – This is called an “output-sensitive” running time, and we’ll see such running times often in the study of data structures. 4

Computing Aggregate Statistics Over a Range • We can count or find the min/max/sum of elements in a range in O(log n) time on a balanced BST. • This works for a dictionary or a sequence encoded within a BST. – On a sequence, we can use this to implement the operations -sum(i, j), range-min(i, j), and range-max(i, j). range • Aggregate all node information at yellow nodes and augmented subtree information at red nodes: LCA(a, b) (possibly succ(a), or alternatively select(i) if encoding a sequence) a b (possibly pred(b), or alternatively select(j) if encoding a sequence) 5

Range Queries in Splay Trees • Range queries (and updates) are particularly nice on splay trees. • Given a range query over [a, b] in a dictionary: – Splay(b) – Splay(a), making sure we perform a single rotation at the root. • This effectively isolates all the elements in (a, b) in a single subtree! a b (possibly succ(a), or alternatively select(i) if encoding a sequence) (possibly pred(b), or alternatively select(j) if encoding a sequence) (a, b) • And this of course works for a sequence too… 6

Static Range Queries in Dictionaries • Input: Set of n numbers (points in 1 dimension). • Common Problems: 1. Tell me all the points in the range [a, b]. 2. Count the number of points in the range [a, b]. • What is the best data structure for (1) and (2) in the static case? 7

Static Range Queries in Dictionaries • Input: Set of n numbers (points in 1 dimension). • Common Problems: 1. Tell me all the points in the range [a, b]. 2. Count the number of points in the range [a, b]. • What is the best data structure for (1) and (2) in the static case? A sorted array! – This solves (1) in O(k + log n) time and (2) in O(log n) time. 8

Databases • Many computing professionals work with large databases. • Structured Query Language (SQL) is a common way to interact with databases. For example: SELECT title, author FROM books_in_library WHERE price <= 100 AND publication date >= 1990 AND page_count BETWEEN 500 AND 750; • Range queries like this can be sped up by telling the database to build indexes (usually a B-trees) on particular fields (e. g. , page_count, price). 9

Multidimensional Range Queries • We can think of the records in a database as points in a high-dimensional space: Age Household income • Example of a multidimensional range query: “Tell me all records with age in the range [18, 24] and household income in the range [$50, 000, $80, 000]”. • Today, we’ll focus on static multidimensional range queries (usually 2 D); no range updates… 10

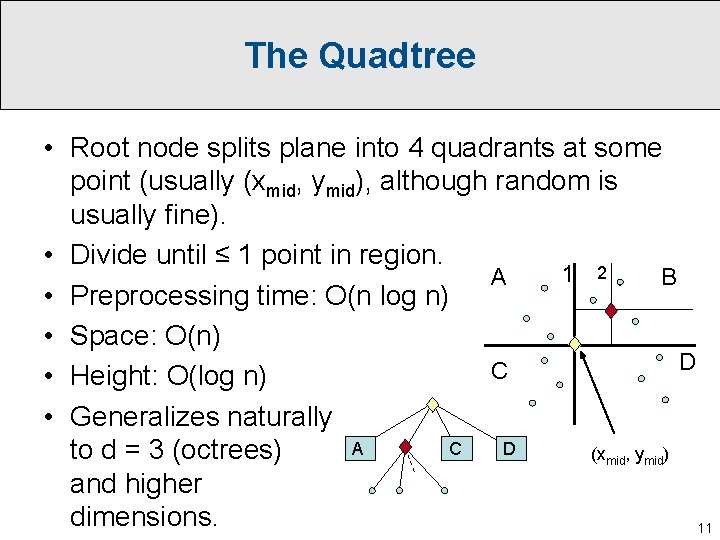
The Quadtree • Root node splits plane into 4 quadrants at some point (usually (xmid, ymid), although random is usually fine). • Divide until ≤ 1 point in region. 1 2 A B • Preprocessing time: O(n log n) • Space: O(n) D C • Height: O(log n) • Generalizes naturally A C D to d = 3 (octrees) (xmid, ymid) and higher dimensions. 11

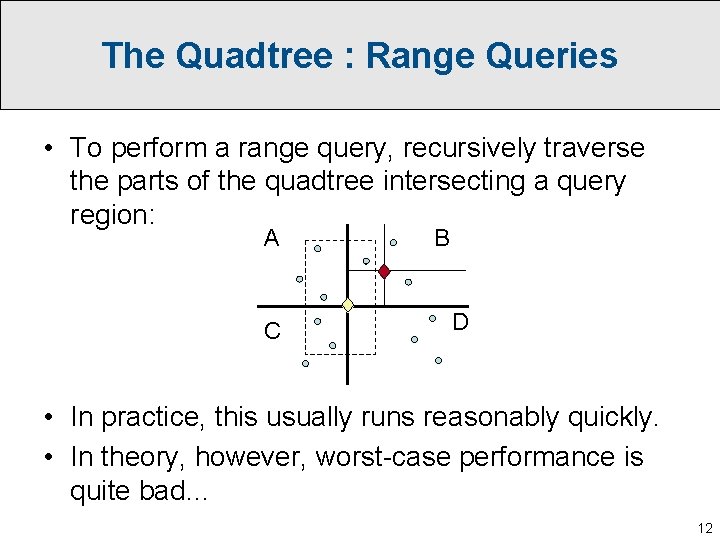
The Quadtree : Range Queries • To perform a range query, recursively traverse the parts of the quadtree intersecting a query region: A C B D • In practice, this usually runs reasonably quickly. • In theory, however, worst-case performance is quite bad… 12

The Quadtree : Range Queries • Bad example of a quadtree query: • Query essentially traverses the entire quadtree, but returns no points. Running time: O(n) 13

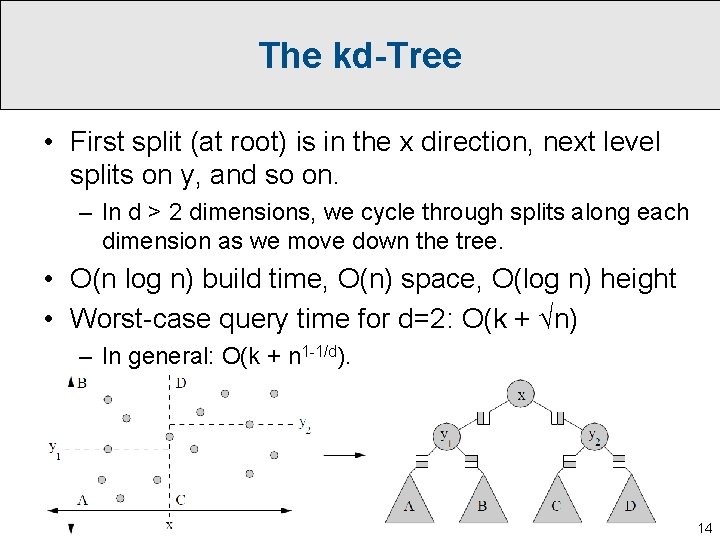
The kd-Tree • First split (at root) is in the x direction, next level splits on y, and so on. – In d > 2 dimensions, we cycle through splits along each dimension as we move down the tree. • O(n log n) build time, O(n) space, O(log n) height • Worst-case query time for d=2: O(k + √n) – In general: O(k + n 1 -1/d). 14

The kd-Tree : Range Queries • Same as with quadtrees: recursively visit all parts of the tree intersecting the query region R: Range. Query(T, R): If T->boundingbox does not intersect R, return If T is a leaf, return the single point (if any) in this leaf if it is contained in R. Otherwise, recursively query the children of T. R 15

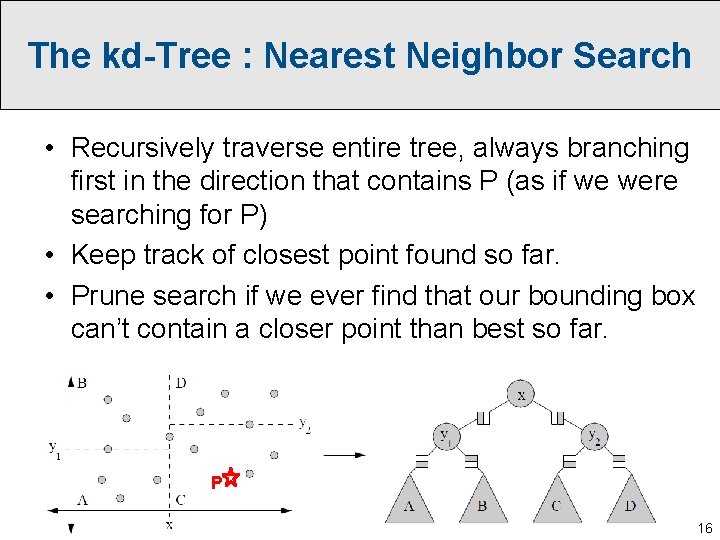
The kd-Tree : Nearest Neighbor Search • Recursively traverse entire tree, always branching first in the direction that contains P (as if we were searching for P) • Keep track of closest point found so far. • Prune search if we ever find that our bounding box can’t contain a closer point than best so far. P 16

k-Nearest Neighbor Search • Recursively traverse entire tree, always branching first in the direction that contains P (as if we were searching for P) • Keep track of closest k points found so far. • Prune search if we ever find that our bounding box can’t contain a closer point than best k so far. P 17

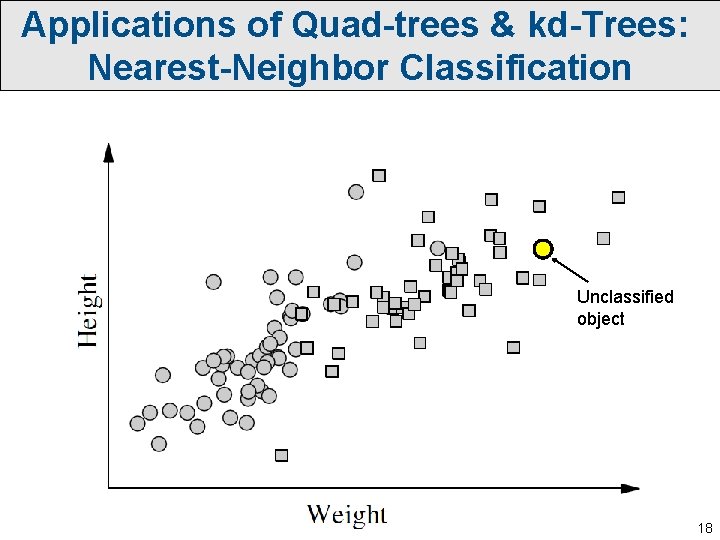
Applications of Quad-trees & kd-Trees: Nearest-Neighbor Classification Unclassified object 18

Related Topic: Mesh Refinement (i. e. , Spatial Decomposition at Varying Resolution) 19

Applications of Quad-trees & kd-Trees: Speeding up Geometric Algorithms 20

Binary Space Partition Trees • Another way to recursively decompose 2 D / 3 D space. • Often used to pre-process a static scene, allowing fast back-to-front rendering from any vantage point. 21

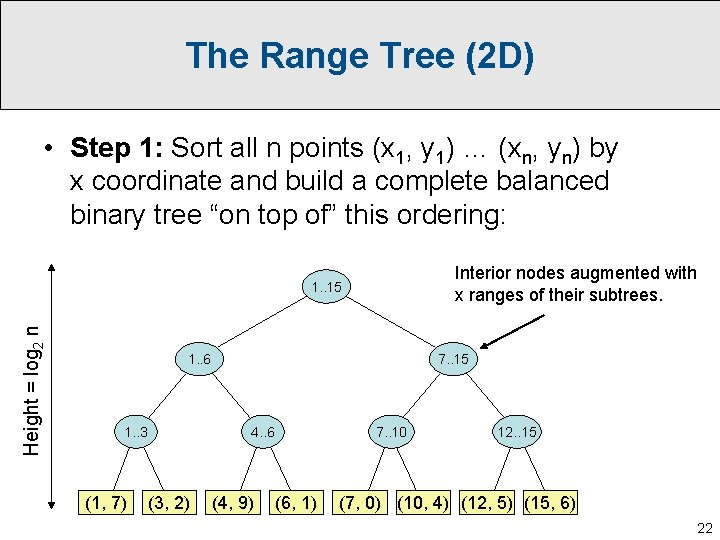
The Range Tree (2 D) • Step 1: Sort all n points (x 1, y 1) … (xn, yn) by x coordinate and build a complete balanced binary tree “on top of” this ordering: Interior nodes augmented with x ranges of their subtrees. Height = log 2 n 1. . 15 1. . 6 1. . 3 (1, 7) 7. . 15 4. . 6 (3, 2) (4, 9) 7. . 10 (6, 1) 12. . 15 (7, 0) (10, 4) (12, 5) (15, 6) 22

The Range Tree (2 D) Height = log 2 n • Recall that we can answer a range query in x with a collection of ≤ 2 log 2 n subtrees: x range query 23

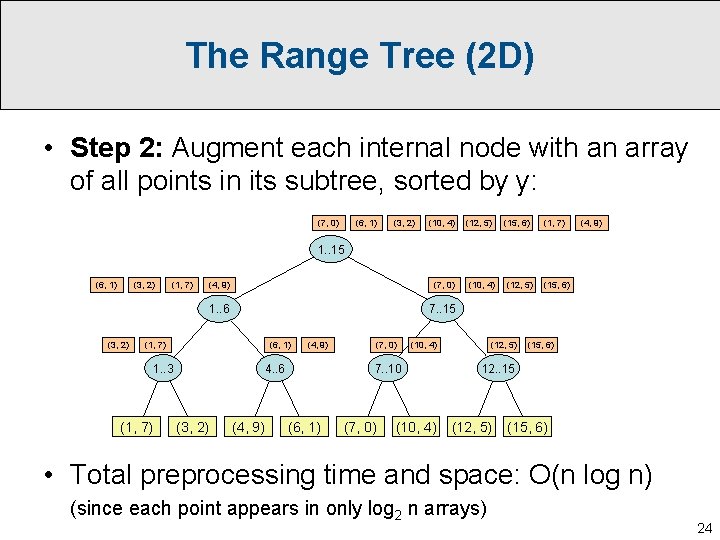
The Range Tree (2 D) • Step 2: Augment each internal node with an array of all points in its subtree, sorted by y: (7, 0) (6, 1) (3, 2) (10, 4) (12, 5) (15, 6) (1, 7) (4, 9) 1. . 15 (6, 1) (3, 2) (1, 7) (4, 9) (7, 0) 1. . 6 7. . 15 (1, 7) (6, 1) 1. . 3 (1, 7) (4, 9) 4. . 6 (3, 2) (4, 9) (7, 0) (10, 4) 7. . 10 (6, 1) (7, 0) (10, 4) (12, 5) (15, 6) 12. . 15 (12, 5) (15, 6) • Total preprocessing time and space: O(n log n) (since each point appears in only log 2 n arrays) 24

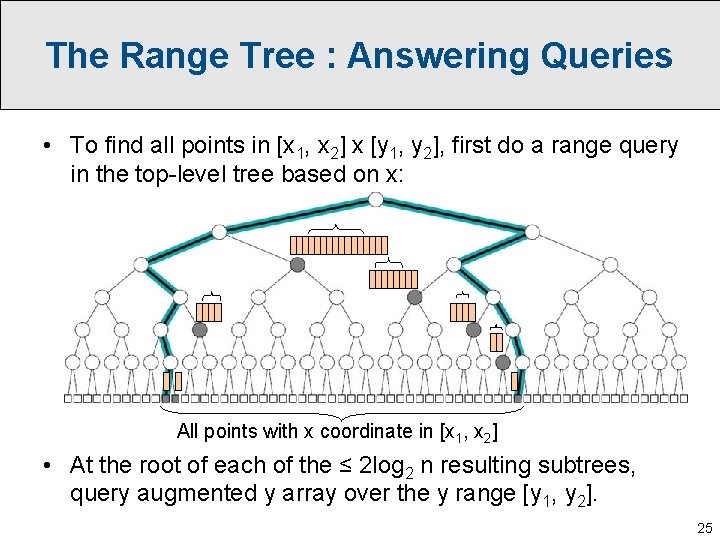
The Range Tree : Answering Queries • To find all points in [x 1, x 2] x [y 1, y 2], first do a range query in the top-level tree based on x: All points with x coordinate in [x 1, x 2] • At the root of each of the ≤ 2 log 2 n resulting subtrees, query augmented y array over the y range [y 1, y 2]. 25

The Range Tree : Query Performance • Each 2 D range query results in our performing 2 log 2 n individual 1 D range queries, each with O(log n) overhead (for a binary search). • Total query time: O(k + log 2 n). • In d dimensions: O(k + logd n). (in a d-dimensional range tree, our top level tree is sorted by 1 st coordinate, and each internal node is augmented with a (d-1)-dimensional range tree built using the other coordinates). 26