Lecture 12 Principles of Mass Balance Box Models

Lecture 12 Principles of Mass Balance Box Models: The modern view about what controls the composition of sea water

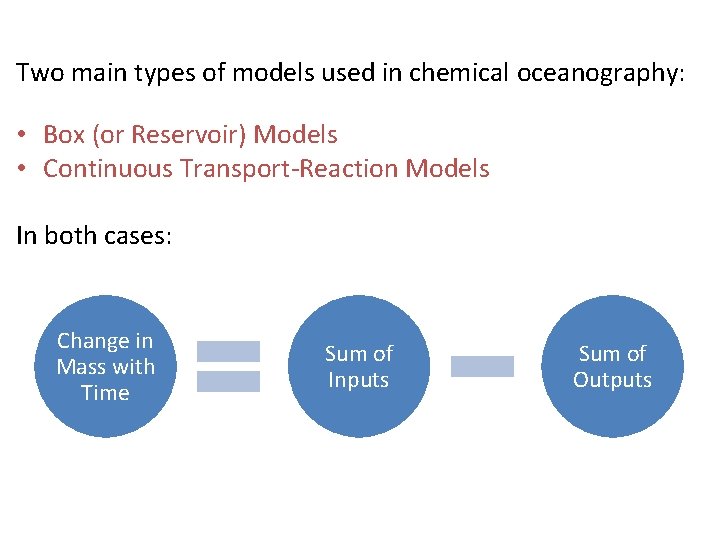
Two main types of models used in chemical oceanography: • Box (or Reservoir) Models • Continuous Transport-Reaction Models In both cases: Change in Mass with Time Sum of Inputs Sum of Outputs

At steady state the dissolved concentration (Mi) does not change with time: (d. M/dt)ocn = Σd. Mi / dt = 0 (i. e. the sum of the sources must equal the sum of the sinks at steady state) Change in Mass with Time = 0 Sum of Inputs Sum of Outputs

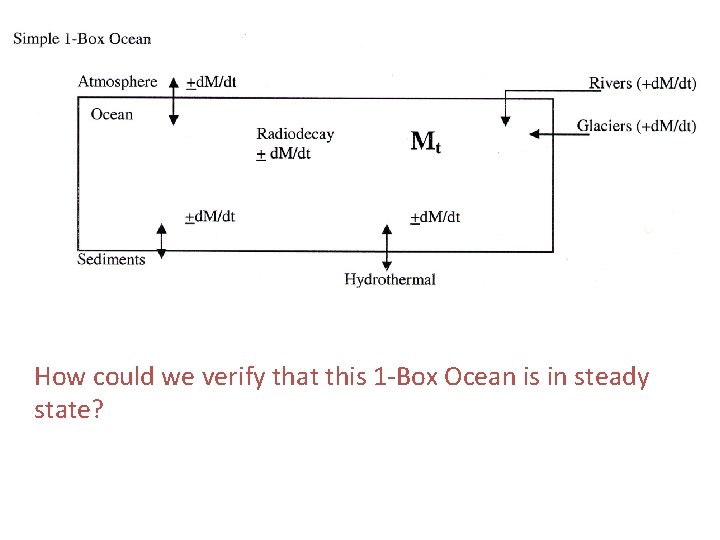
How could we verify that this 1 -Box Ocean is in steady state?

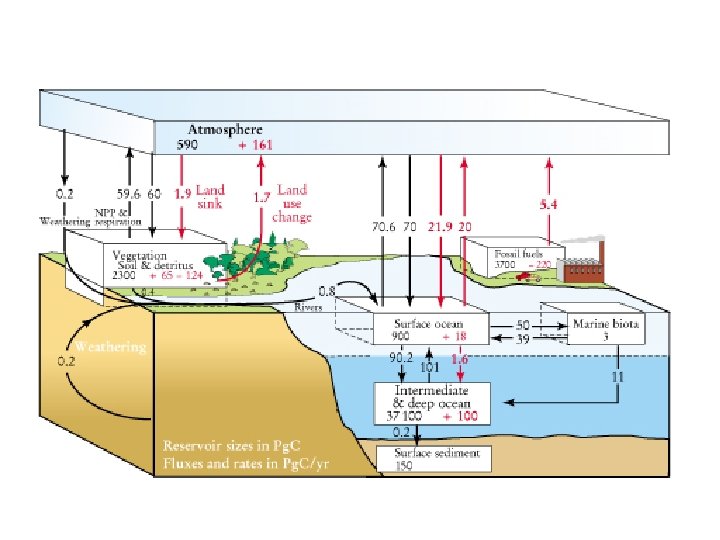
For most elements in the ocean: (d. M/dt)ocn = Fatm + Frivers - Fseds + Fhydrothermal If we assume steady state, and assume atmospheric flux is negligible (safe for most elements)… the main balance is even simpler: Frivers all elements = Fsediment all elements + Fhydrothermal source: Li, Rb, K, Ca, Fe, Mn sink: Mg, SO 4, alkalinity

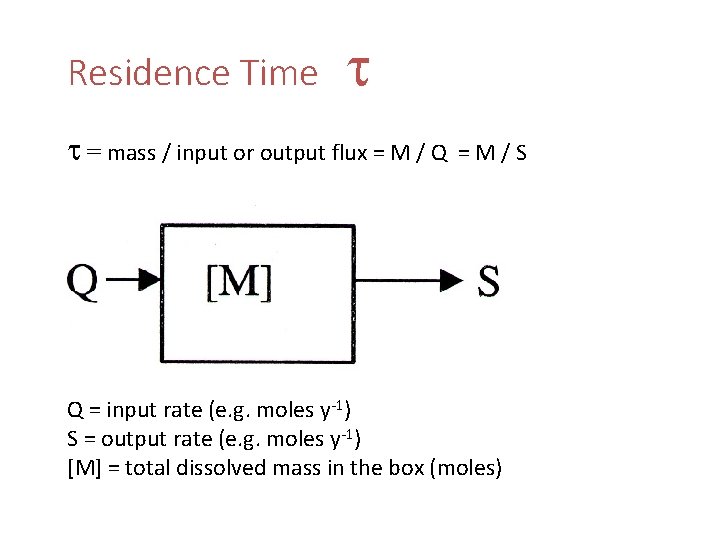
Residence Time = mass / input or output flux = M / Q =M/S Q = input rate (e. g. moles y-1) S = output rate (e. g. moles y-1) [M] = total dissolved mass in the box (moles)

d[M] / dt = Q – S Source = Q = = Sink = S e. g. river input flux Zeroth Order flux (flux is not proportional to how much M is present in the ocean) = many removal mechanisms are First Order (the flux is proportional to how much M is there) (e. g. radioactive decay, plankton uptake, adsorption by particles)

First order removal is proportional to how much is there. S = k [M] where k (sometimes ) is the first order removal rate constant (t-1) and [M] is the total mass. Then, we can rewrite d[M]/dt = Q – S, to include the first order sink: d[M] / dt = Q – k [M] At steady state when d[M]/dt = 0, Q = k[M] Rearrange: [M]/Q = 1/k = * and [M] = Q / k *inverse relationship between first order removal constant and residence time

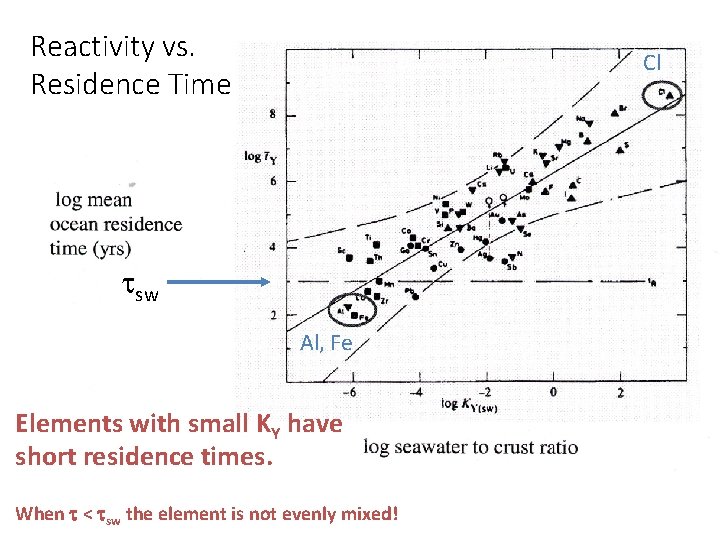
Reactivity vs. Residence Time Cl sw Al, Fe Elements with small KY have short residence times. When < sw the element is not evenly mixed!

Dynamic Box Models In some instances, the source (Q) and sink (S) rates are not constant with time OR they may have been constant, but suddenly change. Examples: Glacial/Interglacial cycles, Anthropogenic Inputs to Ocean Assume that the initial amount of M at t = 0 is Mo. The initial mass balance equation is: d. M/dt = Qo – So = Qo – k Mo The input increases to a new value Q 1. The new balance at steady state is: d. M/dt = Q 1 – k M and the solution for the approach to the new equilibrium state is: M(t) = M 1 – [(M 1 – Mo)e-kt] “M increases from Mo to the new value of M 1 (Q 1/k) with a response time of k-1 or ”

Dynamic Box Models M(t) = M 1 – [(M 1 – Mo)e-kt] = This response time is defined as the time it takes to reduce the imbalance (M 1 – Mo). to e -1 (or 37%) of the initial imbalance ((1/e)*( M – M )). 1 o This response time-scale is referred to as the “e-folding time”. If we assume Mo = 0, after one residence time (t = ) we find that: Mt / M 1 = (1 – e-1) = 0. 63 This is 37% reduced, = e-folding time! For a single box model with a 1 st order sink, response time = residence time. Elements with a short residence time will approach their new value faster than elements with long residence times.

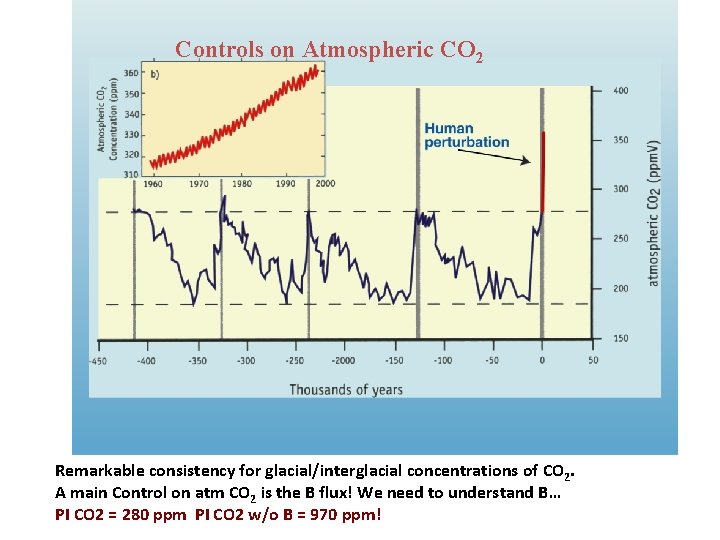
Controls on Atmospheric CO 2 Remarkable consistency for glacial/interglacial concentrations of CO 2. A main Control on atm CO 2 is the B flux! We need to understand B… PI CO 2 = 280 ppm PI CO 2 w/o B = 970 ppm!

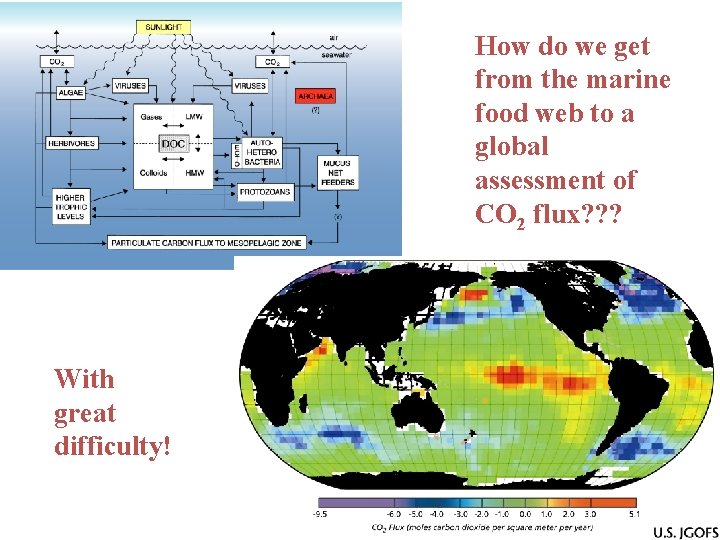
How do we get from the marine food web to a global assessment of CO 2 flux? ? ? With great difficulty!

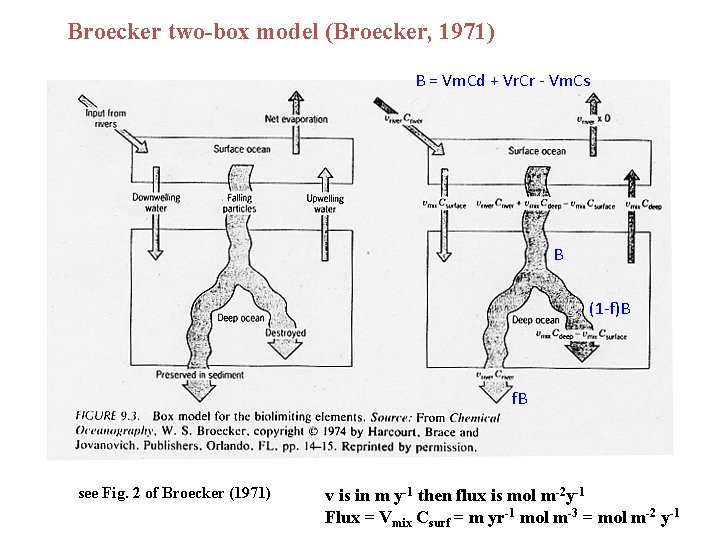
Broecker two-box model (Broecker, 1971) B = Vm. Cd + Vr. Cr - Vm. Cs B (1 -f)B f. B see Fig. 2 of Broecker (1971) v is in m y-1 then flux is mol m-2 y-1 Flux = Vmix Csurf = m yr-1 mol m-3 = mol m-2 y-1

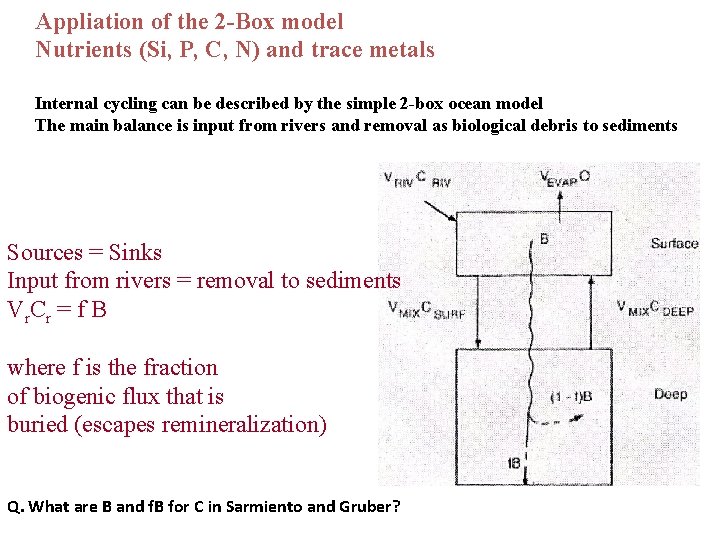
Appliation of the 2 -Box model Nutrients (Si, P, C, N) and trace metals Internal cycling can be described by the simple 2 -box ocean model The main balance is input from rivers and removal as biological debris to sediments Sources = Sinks Input from rivers = removal to sediments V r. C r = f B where f is the fraction of biogenic flux that is buried (escapes remineralization) Q. What are B and f. B for C in Sarmiento and Gruber?

Broecker (1971) defines some parameters for the 2 -box model Two important parameters are g and f: g = the fraction of an element put in at the surface that is removed as B (the efficiency of bioremoval of an element from the surface – how efficiently it sinks as a particle (as B flux) out of the surface ocean) = B / surface ocean input = (Vmix. CD + Vr. Cr – Vmix. Cs) / Vmix. Cd + Vr. Cr f = = the fraction of particles that are buried (the efficiency of ultimate removal from the water column) Vr. Cr / B = Vr. Cr / (Vmix. Cd + Vr. Cr - Vmix. Cs)

Broecker (1971) defines some parameters for the 2 -box model g = B / input = (Vmix. CD + Vr. Cr – Vmix. Cs) / Vmix. Cd + Vr. Cr f = Vr. Cr / B = Vr. Cr / (Vmix. Cd + Vr. Cr - Vmix. Cs) fraction of input to surface removed as B because f. B = Vr. Cr fraction of element removed to sediment per visit to the surface fxg In this model Vr = 10 cm y-1 Vmix = 200 cm y-1 so Vmix / Vr = 20 Here are some values: g f fxg N 0. 95 0. 01 P 0. 95 0. 01 C 0. 20 0. 02 0. 004 Si 1. 0 0. 01 Ba 0. 75 0. 12 0. 09 Ca 0. 01 0. 12 0. 001 See Broecker (1971) Table 3 From 14 C mass balance (next slide) Q. Explain these values and why they vary the way they do.

How large is the transport term: If the residence time of the deep ocean is 1850 yrs (from 14 C) and = Vold / Vmix fraction of total depth volume that is deep ocean then: Vmix = (3700 m/3800 m)(1. 37 x 1018 m 3) / 1850 y = 0. 72 x 1015 m 3 y-1 If River Inflow = 3. 7 x 1013 m 3 y-1 Then River Inflow / Deep Box Exchange = 3. 7 x 1013/72 x 1013 = 1 / 19. 5 This means water circulates on average about 19. 5 times through the ocean (surface to deep exchange) before it evaporates and returns as river flow.

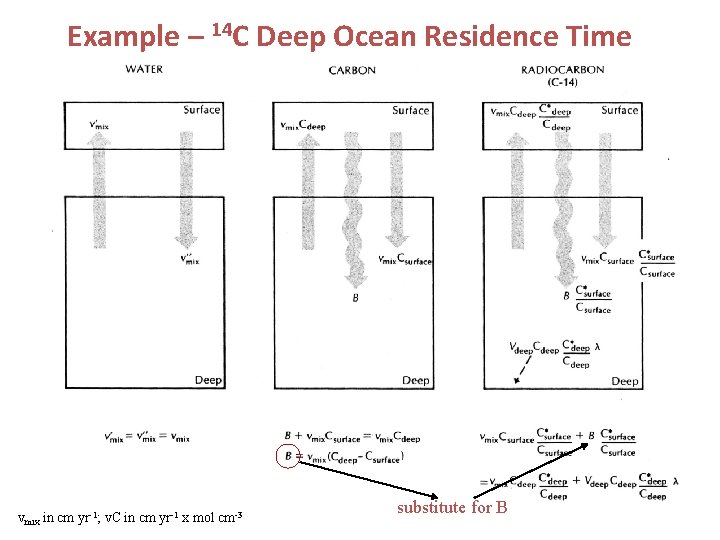
Example – 14 C Deep Ocean Residence Time vmix in cm yr-1; v. C in cm yr-1 x mol cm-3 substitute for B

Rearrange and Solve for Vmix Use pre-nuclear 14 C data when surface 14 C > deep 14 C (14 C/C)deep = 0. 81 (14 C/C)surf Vmix = (200 cm y-1) A for h = 3700 m A = ocean area thus age of deep ocean box (t) t = 3700 m / 2 my-1 = 1850 years

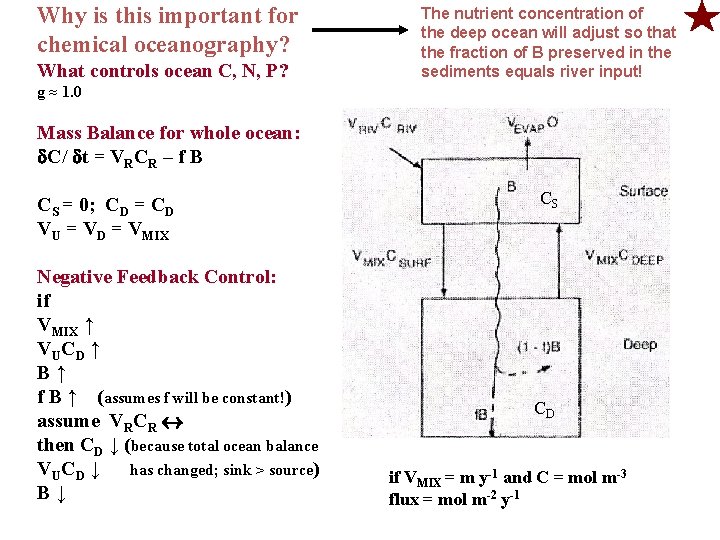
Why is this important for chemical oceanography? What controls ocean C, N, P? The nutrient concentration of the deep ocean will adjust so that the fraction of B preserved in the sediments equals river input! g ≈ 1. 0 Mass Balance for whole ocean: C/ t = VRCR – f B CS = 0; CD = CD VU = VD = VMIX Negative Feedback Control: if VMIX ↑ VUCD ↑ B↑ f B ↑ (assumes f will be constant!) assume VRCR then CD ↓ (because total ocean balance VUCD ↓ has changed; sink > source) B↓ CS CD if VMIX = m y-1 and C = mol m-3 flux = mol m-2 y-1

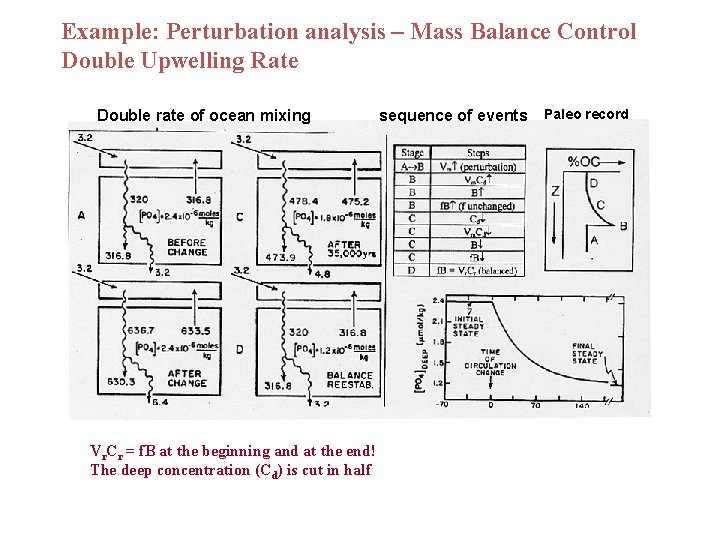
Example: Perturbation analysis – Mass Balance Control Double Upwelling Rate Double rate of ocean mixing Vr. Cr = f. B at the beginning and at the end! The deep concentration (Cd) is cut in half sequence of events Paleo record

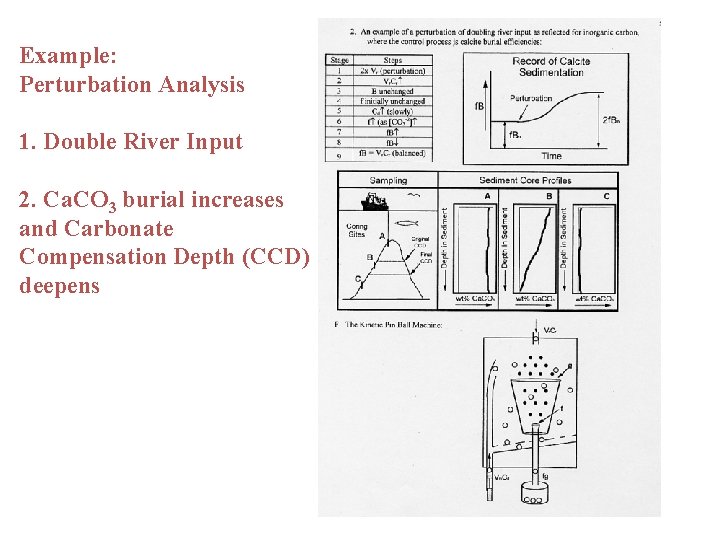
Example: Perturbation Analysis 1. Double River Input 2. Ca. CO 3 burial increases and Carbonate Compensation Depth (CCD) deepens