Lecture 12 Matter waves Quantum mechanics D Aims

Lecture 12 Matter waves (Quantum mechanics). D Aims: Massive particles as dispersive waves. >Phase and group velocity >Evanescent waves (tunneling). >Schrödinger equation. >Time-dependent equation; >Time-independent equation. >Interpretation of the wave function. >Heisenberg’s Uncertainty Principle. >Applications: >Reflection/transmission at potential step. >1 -D potential well >Energy quantisation 1 Waves 11

Matter waves D de Broglie (1924) ë Proposed wavelike properties for particles (since light showed particle properties) ë de Broglie wavelength l = h/p (or ) D Davisson and Germer (1927) ë Electron diffraction. Now the basis of the use of LEED (Low Energy Electron Diffraction) as a probe for surface structure. ë At 100 e. V, K. E. =p 2/2 m is such that p=5. 4 x 10 -24 Kg m s-1. l=1. 2 x 10 -10 m, i. e. of order of atomic dimensions. ë GP Thompson (1927) directed 15 ke. V electrons through a thin metal foil. Again discrete scattering angles were observed. 2 Waves 11

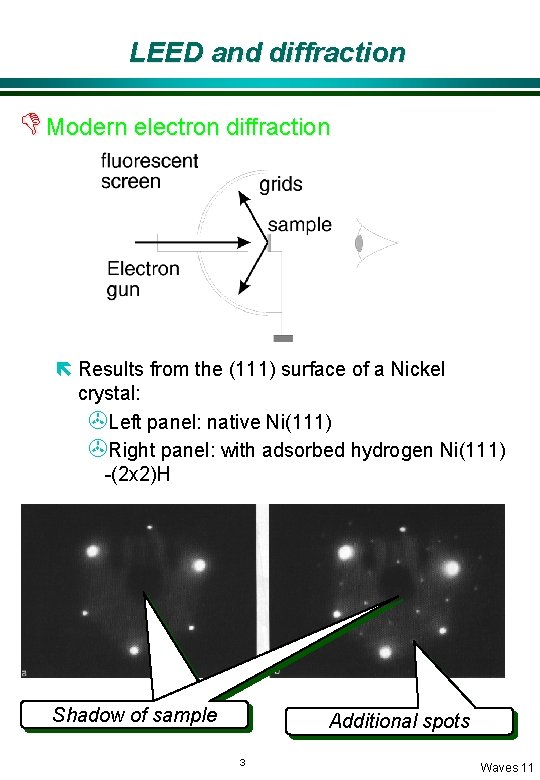
LEED and diffraction D Modern electron diffraction ë Results from the (111) surface of a Nickel crystal: >Left panel: native Ni(111) >Right panel: with adsorbed hydrogen Ni(111) -(2 x 2)H Shadow of sample Additional spots 3 Waves 11

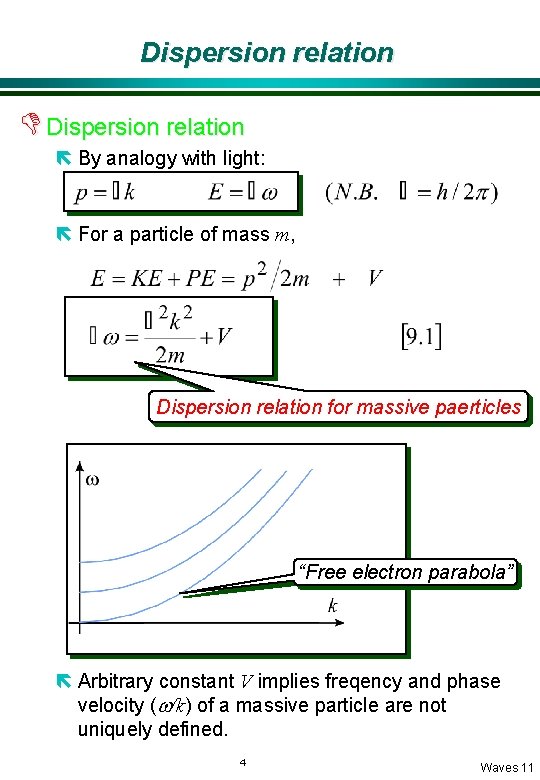
Dispersion relation D Dispersion relation ë By analogy with light: ë For a particle of mass m, Dispersion relation for massive paerticles “Free electron parabola” ë Arbitrary constant V implies freqency and phase velocity (w/k) of a massive particle are not uniquely defined. 4 Waves 11

Group velocity D Group velocity ë follows from the dispersion relation: Classical velocity of the particle ë The same is true relativistically. D Classiclly forbidden region. ë Classically, particles cannot enter regions where their total energy, E, is less than V. ë Under such circumstances, eq [9. 1] gives where a is real ë The wave becomes evanescent. ë The wave penetrates into the classically forbidden region but the amplitude decays exponentially. 5 Waves 11

Schrödinger equation D “Derivation” ë Start from expression for the energy of a nonrelativistic particle ë Take a plane wave (travelling in +ve x-direction) (note we use the Q. M. “convention” of kx-wt) Inserting into [9. 2] and multiplying by Y gives: ë Time dependent Schrödinger equation ë It is a linear equation so we can superpose solutions 6 Waves 11

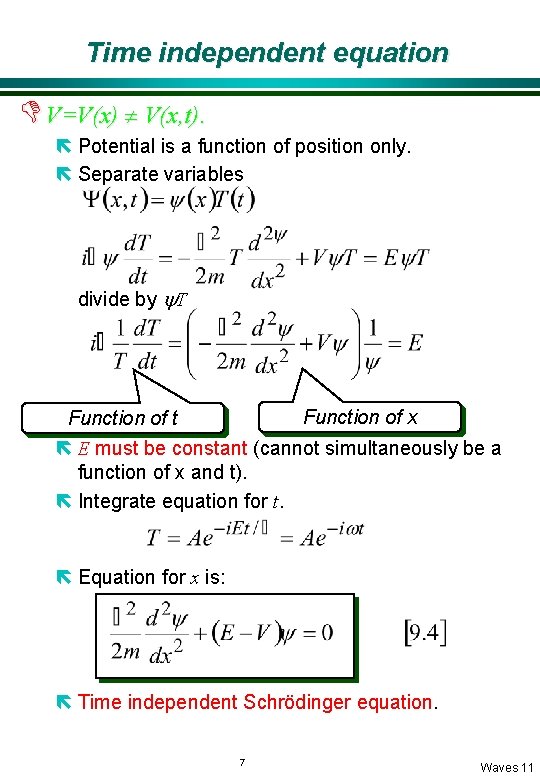
Time independent equation D V=V(x) ¹ V(x, t). ë Potential is a function of position only. ë Separate variables divide by y. T Function of x Function of t ë E must be constant (cannot simultaneously be a function of x and t). ë Integrate equation for t. ë Equation for x is: ë Time independent Schrödinger equation. 7 Waves 11

Wave function D Interpretation ë Born (1927): The probability that a particle with wave function Y(x, t) will be found at a position between x and x+dx at time t is given by |Y(x, t)|2 dx. ë Normalisation Particle must be somewhere ë Y itself is unobservable, only |Y|2 has physical significance. ë Plane wave: complex form of Y is necessary (not a mathematical convenience) to ensure uniform probability. 8 Waves 11

Heisenberg’s Uncertainty Principle D Localised wavepacket ë Probability of finding particle localised in space. ë MUST be a corresponding spread in the Fourier Transform. ë Wavepacket of width Dx corresponds to Dk~2 p/Dx. ë It is impossible to measure the position and momentum of a particle with arbitrary precision simultaneously. ë Since particles with mass are dispersive waves, the packet will spread with time and the particle becomes less well localised. ë Uncertainty in k means we loose knowledge of the particle’s position as time goes on. ë Computer animation. 9 Waves 11

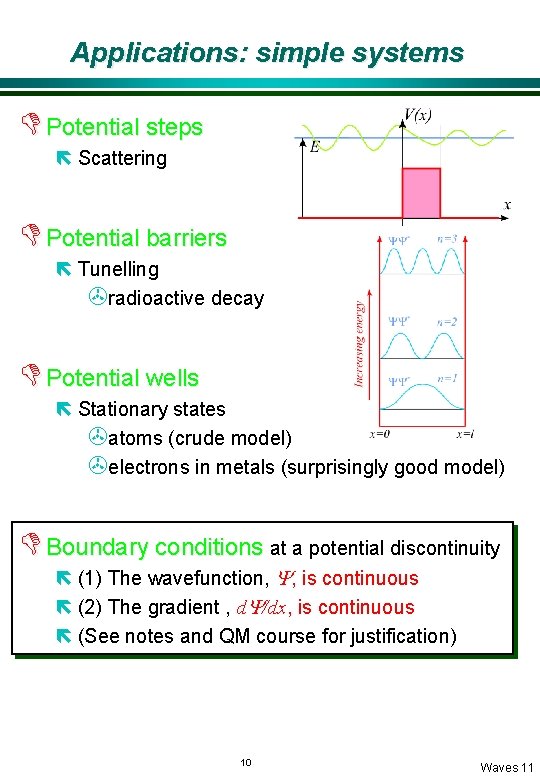
Applications: simple systems D Potential steps ë Scattering D Potential barriers ë Tunelling >radioactive decay D Potential wells ë Stationary states >atoms (crude model) >electrons in metals (surprisingly good model) D Boundary conditions at a potential discontinuity ë (1) The wavefunction, Y, is continuous ë (2) The gradient , d. Y/dx, is continuous ë (See notes and QM course for justification) 10 Waves 11

Reflection/transmission D Finite potential step. ë ë Boundary conditions at x=0. Y continuous A+r=t dy/dx continuous ik 1 A-ik 1 r=ik 2 t ë Vo<0. Classical: accelerate, (no reflection) >Q. M. : Some reflection; phase change of p. ë 0<Vo<E. Classical: decelerate, (no reflection) >Q. M. : Some reflection. ë Vo>E. Classically forbidden, all reflect. >Q. M. : y a e-ax penetrates barrier. i. e. finite probability for being in classically forbidden region, though all reflect. 11 Waves 11

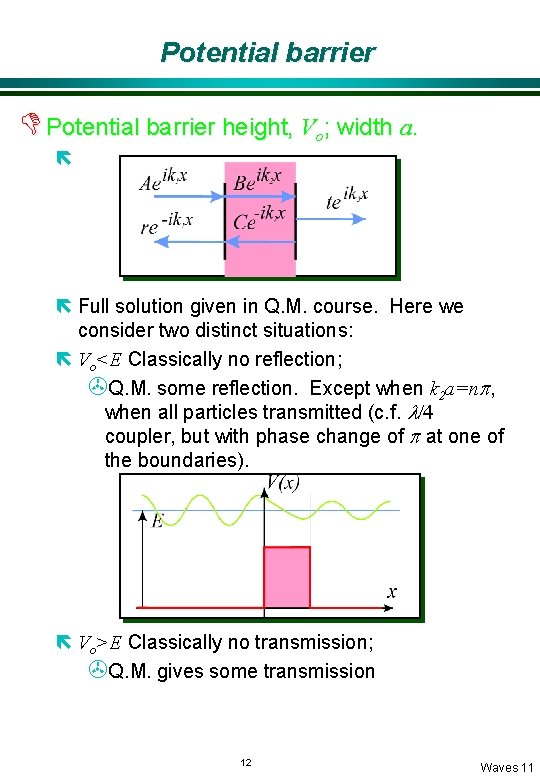
Potential barrier D Potential barrier height, Vo; width a. ë ë Full solution given in Q. M. course. Here we consider two distinct situations: ë Vo<E Classically no reflection; >Q. M. some reflection. Except when k 2 a=np, when all particles transmitted (c. f. l/4 coupler, but with phase change of p at one of the boundaries). ë Vo>E Classically no transmission; >Q. M. gives some transmission 12 Waves 11

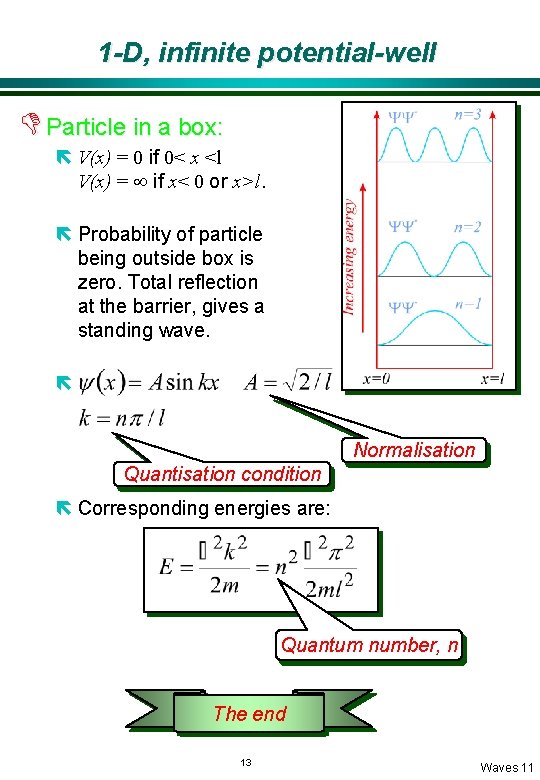
1 -D, infinite potential-well D Particle in a box: ë V(x) = 0 if 0< x <l V(x) = ¥ if x< 0 or x>l. ë Probability of particle being outside box is zero. Total reflection at the barrier, gives a standing wave. ë Normalisation Quantisation condition ë Corresponding energies are: Quantum number, n The end 13 Waves 11