Lecture 12 Introduction to Discrete Fourier Transform Sections

Lecture 12: Introduction to Discrete Fourier Transform Sections 2. 2. 3, 2. 3

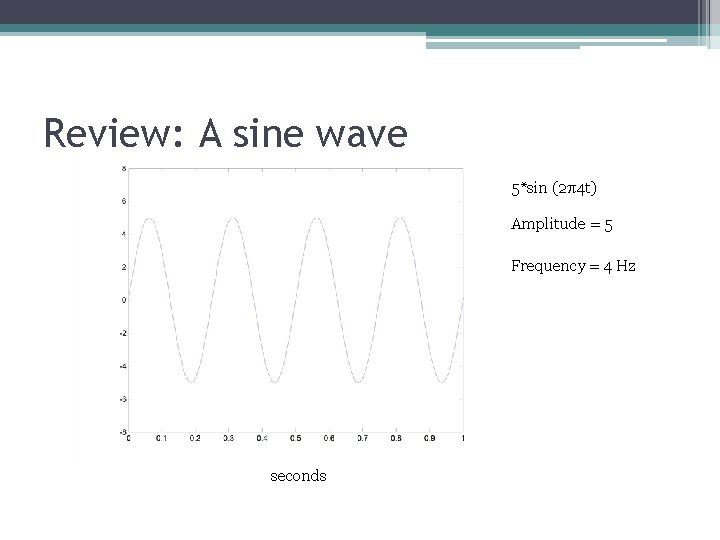
Review: A sine wave 5*sin (2 4 t) Amplitude = 5 Frequency = 4 Hz seconds

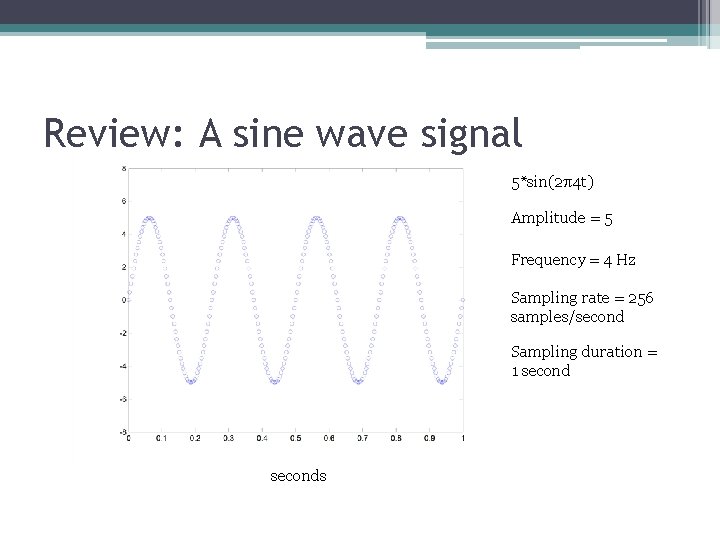
Review: A sine wave signal 5*sin(2 4 t) Amplitude = 5 Frequency = 4 Hz Sampling rate = 256 samples/second Sampling duration = 1 seconds

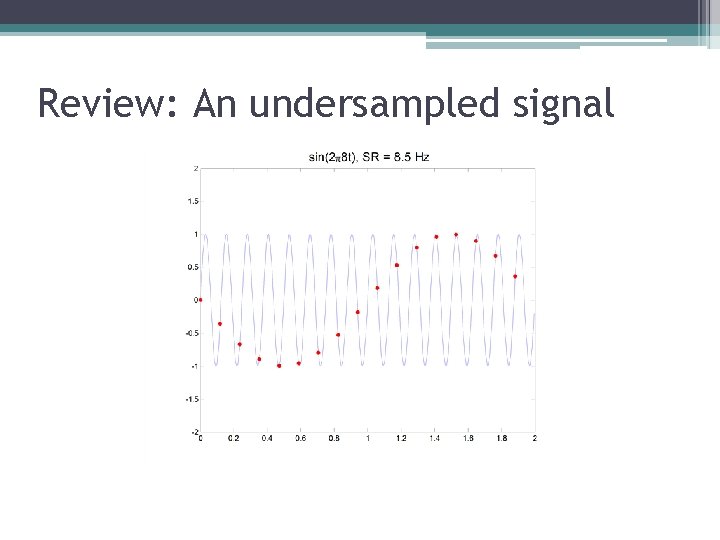
Review: An undersampled signal

Review: The Nyquist Frequency • The Nyquist frequency is equal to one-half of the sampling frequency. • The Nyquist frequency is the highest frequency that can be measured in a signal.

The Fourier Transform • A transform takes one function (or signal) and turns it into another function (or signal) • Continuous Fourier Transform: close your eyes if you don’t like integrals

The Fourier Transform • A transform takes one function (or signal) and turns it into another function (or signal) • The Discrete Fourier Transform:

Fast Fourier Transform • The Fast Fourier Transform (FFT) is a very efficient algorithm for performing a discrete Fourier transform • FFT principle first used by Gauss in 18? ? • FFT algorithm published by Cooley & Tukey in 1965 • In 1969, the 2048 point analysis of a seismic trace took 13 ½ hours. Using the FFT, the same task on the same machine took 2. 4 seconds!

Famous Fourier Transforms Sine wave Delta function

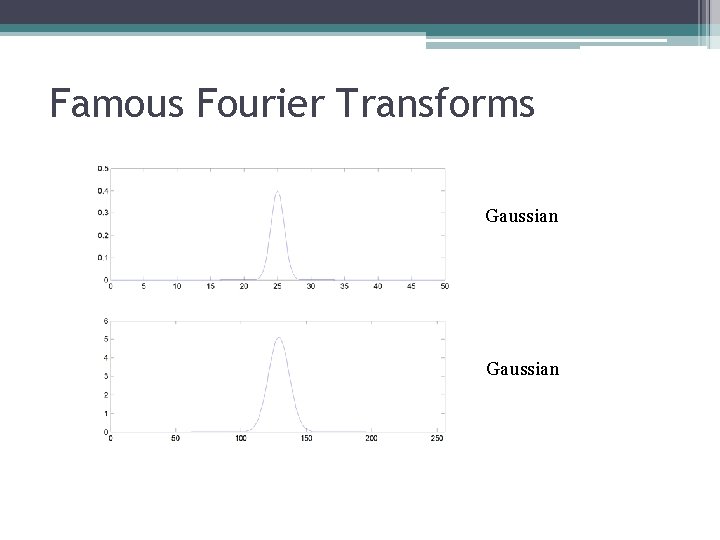
Famous Fourier Transforms Gaussian

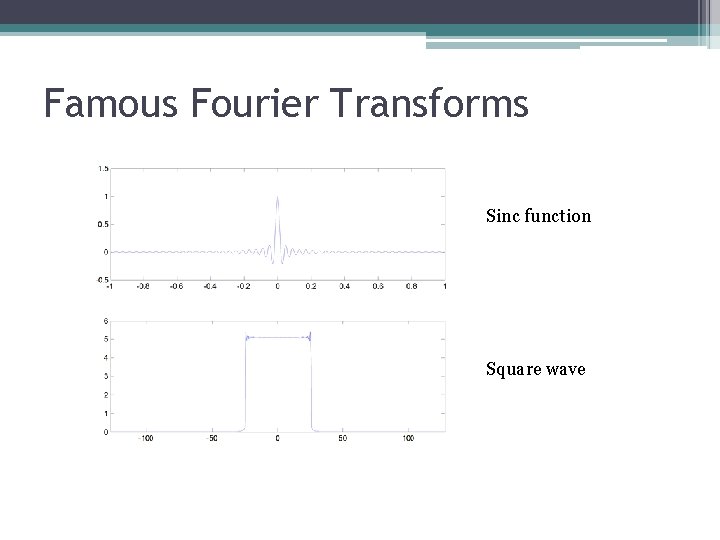
Famous Fourier Transforms Sinc function Square wave

Famous Fourier Transforms Sinc function Square wave

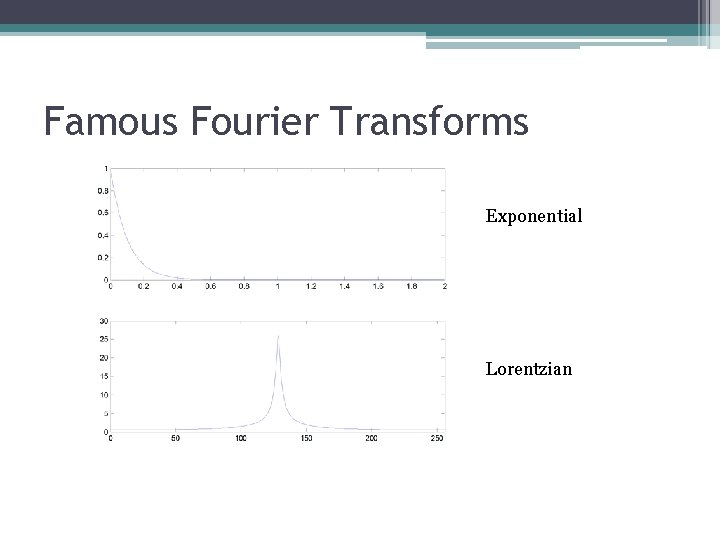
Famous Fourier Transforms Exponential Lorentzian

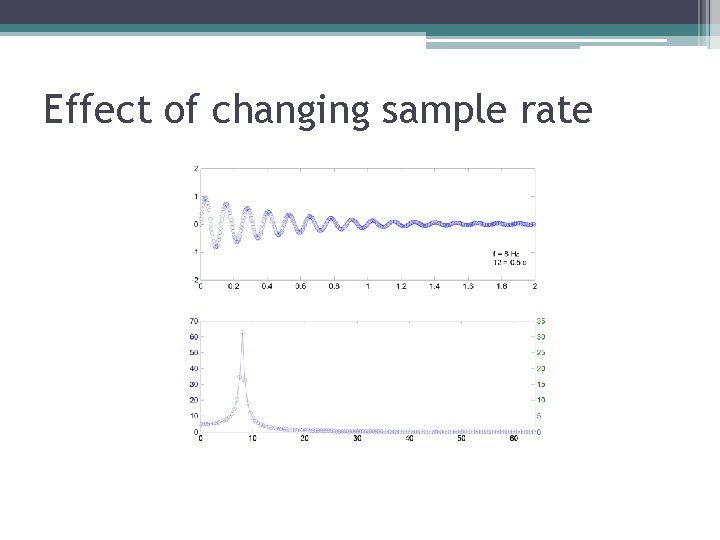
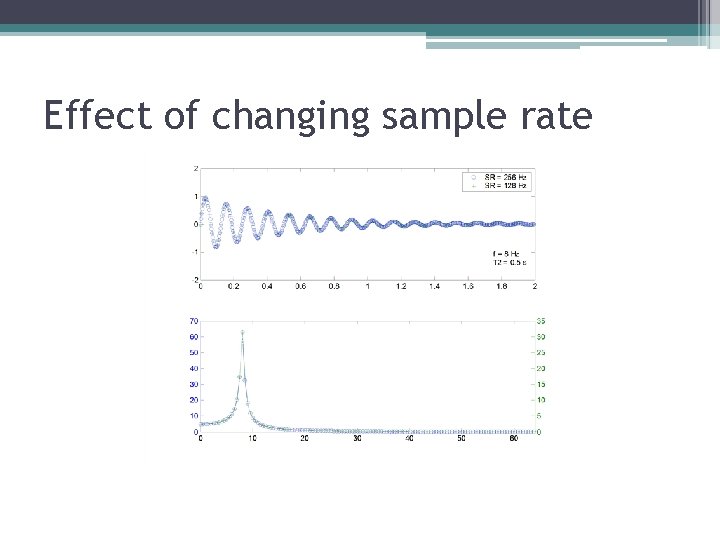
Effect of changing sample rate

Effect of changing sample rate

Effect of changing sample rate • Lowering the sample rate: ▫ Reduces the Nyquist frequency, which ▫ Reduces the maximum measurable frequency ▫ Does not affect the frequency resolution

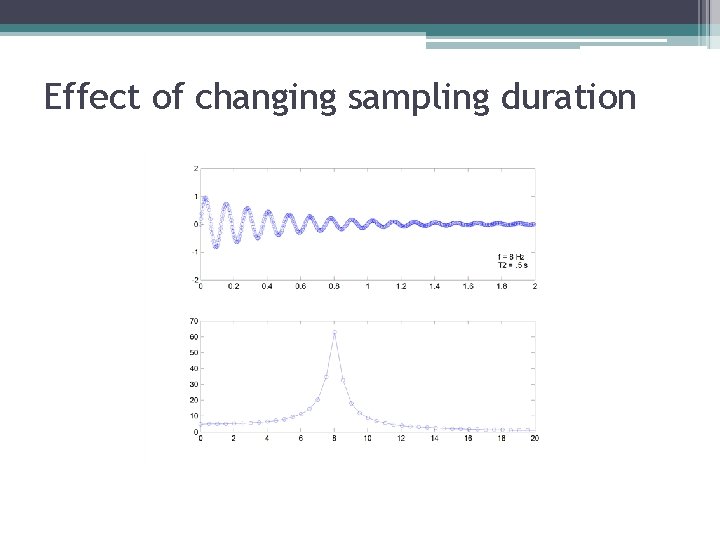
Effect of changing sampling duration

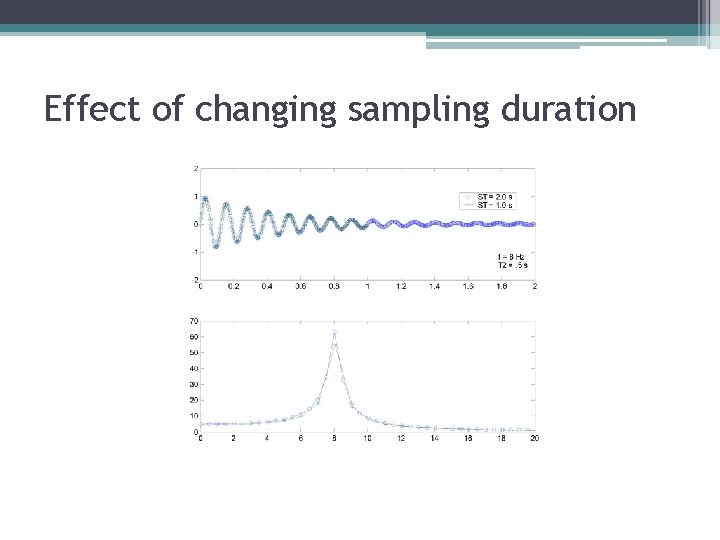
Effect of changing sampling duration

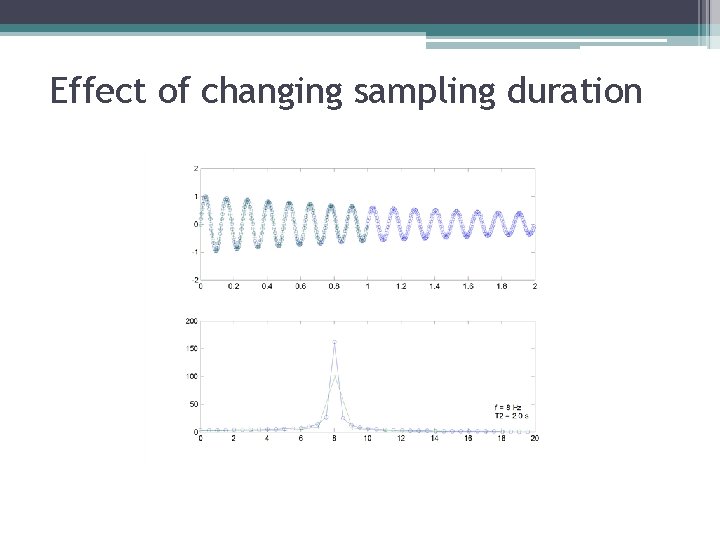
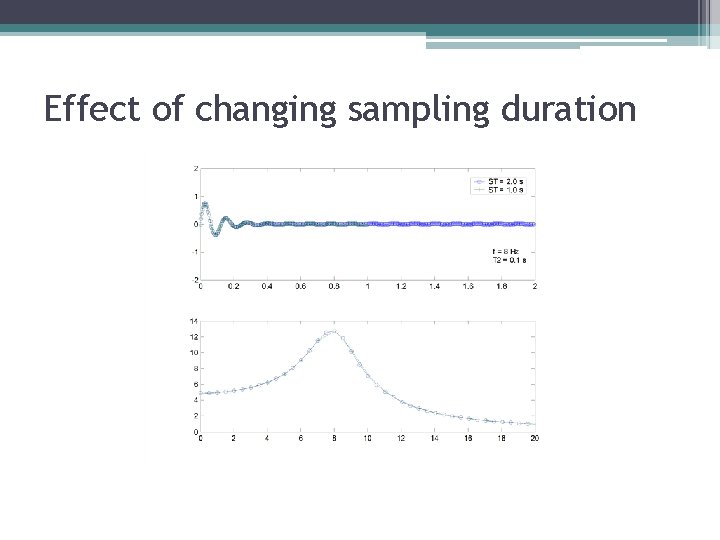
Effect of changing sampling duration • Reducing the sampling duration: ▫ Lowers the frequency resolution ▫ Does not affect the range of frequencies you can measure

Effect of changing sampling duration

Effect of changing sampling duration

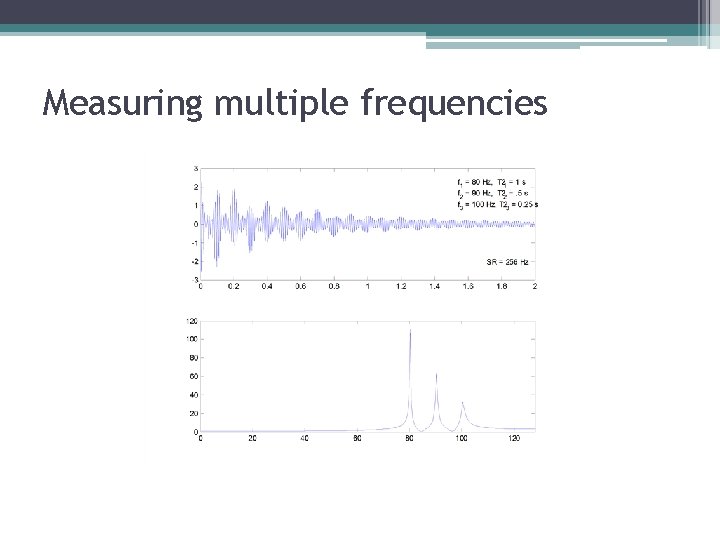
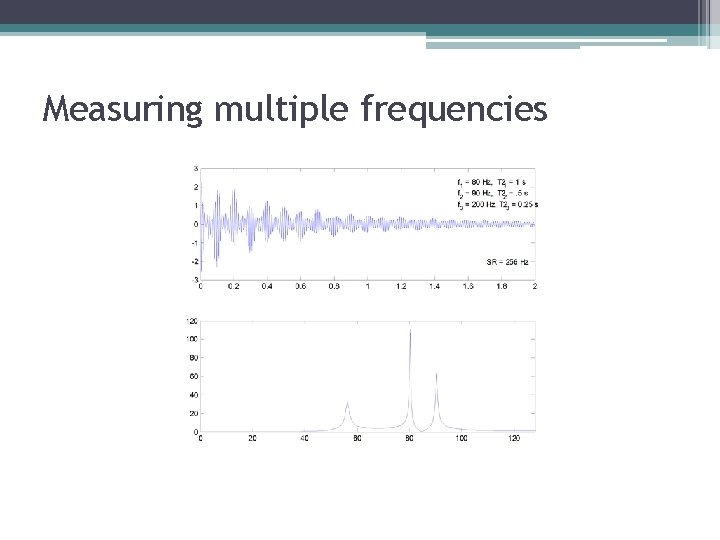
Measuring multiple frequencies

Measuring multiple frequencies

FFT in matlab • Assign your time variables ▫ t = [0: 255]; • Assign your function ▫ y = cos(2*pi*n/10); • Choose the number of points for the FFT (preferably a power of two) ▫ N = 2048; • Use the command ‘fft’ to compute the N-point FFT for your signal ▫ Yf = abs(fft(y, N)); • Use the ‘fftshift’ command to shift the zero-frequency component to center of spectrum for better visualization of your signals spectrum ▫ Yf= fftshift(Yf); • Assign your frequency variable which is your x-axis for the spectrum ▫ f = [-N/2: N/2 -1]/N; - this is the normalized frequency symmetrical about f 0 and about the y-axis • Plot the spectrum ▫ plot(f, Yf)

FFT in matlab • Vary the sampling frequency and see what happens • Vary the sample duration and see what happens

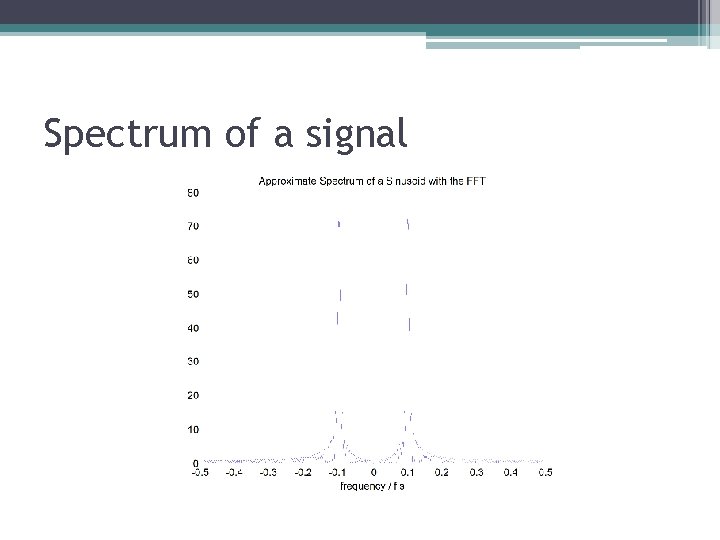
Spectrum of a signal