Lecture 12 Dimensional Analysis And Similitude Model Analysis

Lecture # 12

Dimensional Analysis And Similitude & Model Analysis

Dimensional Analysis n n n Introduction: Dimensional analysis is a mathematical technique making use of study of dimensions. This mathematical technique is used in research work for design and for conducting model tests. It deals with the dimensions of physical quantities involved in the phenomenon. All physical quantities are measured by comparison, which is made with respect to an arbitrary fixed value. In dimensional analysis one first predicts the physical parameters that will influence the flow, and then by, grouping these parameters in dimensionless combinations a better understanding of the flow phenomenon is made possible. It is particularly helpful in experimental work because it provides a guide to those things that significantly influence the phenomena; thus it indicates the direction in which the experimental work should go.

Types of Dimensions n There are two types of dimensions ¨ Fundamental Dimensions or Fundamental Quantities ¨ Secondary Dimensions or Derived Quantities n Fundamental Dimensions or Fundamental Quantities: These are basic quantities. For Example; ¨ Time, T ¨ Distance, L ¨ Mass, M

Types of Dimensions n Secondary Dimensions or Derived Quantities n The are those quantities which possess more than one fundamental dimension. n For example; Velocity is denoted by distance per unit time L/T ¨ Acceleration is denoted by distance per unit time square L/T 2 ¨ Density is denoted by mass per unit volume M/L 3 ¨ n Since velocity, density and acceleration involve more than one fundamental quantities so these are called derived quantities.

Methodology of Dimensional Analysis n The Basic principle is Dimensional Homogeneity, which means the dimensions of each terms in an equation on both sides are equal. n So such an equation, in which dimensions of each term on both sides of equation are same, is known as Dimensionally Homogeneous equation. Such equations are independent of system of units. For example; n Lets consider the equation V=(2 g. H)1/2 Dimensions of LHS=V=L/T=LT-1 ¨ Dimensions of RHS=(2 g. H)1/2=(L/T 2 x. L)1/2=LT-1 ¨ Dimensions of LHS= Dimensions of RHS ¨ n So the equation V=(2 g. H)1/2 homogeneous equation. is dimensionally

Methods of Dimensional Analysis n If the number of variables involved in a physical phenomenon are known, then the relation among the variables can be determined by the following two methods; ¨ Rayleigh’s Method ¨ Buckingham’s π-Theorem n Rayleigh’s Method: n It is used for determining expression for a variable (dependent) which depends upon maximum three to four variables (Independent) only. If the number of independent variables are more than 4 then it is very difficult to obtain expression for dependent variable. Let X is a dependent variable which depends upon X 1, X 2, and X 3 as independent variables. Then according to Rayleigh’s Method n n X=f(X 1, X 2, X 3) X=K X 1 a, X 2 b, X 3 c which can be written as Where K is a constant and a, b, c are arbitrary powers which are obtained by comparing the powers of fundamental dimensions.

Rayleigh’s Method n n Q. The resisting force R of a supersonic plane during flight can be considered as dependent upon the length of the aircraft l, velocity V, air viscosity μ, air density ρ, and bulk modulus of air k. Express the functional relationship between the variables and the resisting force. Solution:

Rayleigh’s Method

Buckingham’s π-Theorem: n n n Buckingham’s π-Theorem: Since Rayleigh’s Method becomes laborious if variables are more than fundamental dimensions (MLT), so the difficulty is overcome by Buckingham’s πTheorem which states that “If there are n variables (Independent and Dependent) in a physical phenomenon and if these variables contain m fundamental dimensions then the variables are arranged into (n-m) dimensionless terms which are called π-terms. ” Let X 1, X 2, X 3, …, X 4, Xn are the variables involved in a physical problem. Let X 1 be the dependent variable and X 2, X 3, X 4, …, Xn are the independent variables on which X 1 depends. Mathematically it can be written as X 1=f(X 2 , X 3 , X 4 , Xn) which can be rewritten as f 1(X 1, X 2 X 3 X 4 Xn)=0 n n Above equation is dimensionally homogenous. It contain n variables and if there are m fundamental dimensions then it can be written in terms of dimensions groups called π-terms which are equal to (n-m) Hence f 1(π1 π2 π3, … πn-m)=0

Buckingham’s n π-Theorem: Properties of π-terms: Each π-term is dimensionless and is independent of system of units. ¨ Division or multiplication by a constant does not change the character of the π-terms. ¨ Each π-term contains m+1 variables, where m is the number of fundamental dimensions and also called repeating variable. n Let in the above case X 2, X 3, X 4 are repeating variables and if fundamental dimensions m=3 then each π-term is written as Π 1=X 2 a 1. X 3 b 1. X 4 a 1. X 1 Π 2=X 2 a 2. X 3 b 2. X 4 a 2. X 5. . Πn-m=X 2 a(n-m). X 3 b(n-m). X 4 a(n-m). Xn Each equation is solved by principle of dimensionless homogeneity and values of a 1, b 1 & c 1 etc are obtained. Final result is in the form of ¨ Π 1=(Π 2, Π 3, Π 4 , …, Π(n-m)) Π 2=(Π 1, Π 3, Π 4 , …, Π(n-m))

Methods of Selecting Repeating Variables n The number of repeating variables are equal to number of fundamental dimensions of the problem. The choice of repeating variables is governed by following considerations; ¨ ¨ ¨ n As far as possible, dependent variable should’t be selected as repeating variable The repeating variables should be chosen in such a way that one variable contains geometric property, other contains flow property and third contains fluid property. The repeating variables selected should form a dimensionless group The repeating variables together must have the same number of fundamental dimension. No two repeating variables should have the same dimensions. Note: In most of fluid mechanics problems, the choice of repeating variables may be (i) d, v ρ, (ii) l, v, ρ or (iii) d, v, μ.

Buckingham’s π-Theorem: n Q. The resisting force R of a supersonic plane during flight can be considered as dependent upon the length of the aircraft l, velocity V, air viscosity μ, air density ρ, and bulk modulus of air k. Express the functional relationship between the variables and the resisting force.

Buckingham’s π-Theorem: n Now each Pi-term is solved by the principle of dimensional homogeneity

Buckingham’s π-Theorem:

Similitude and Model Analysis n Similitude is a concept used in testing of Engineering Models. n Usually, it is impossible to obtain a pure theoretical solution of hydraulic phenomenon. n Therefore experimental investigations are often performed on small scale models, called model analysis. n A few examples, where models may be used are ships in towing basins, air planes in wind tunnel, hydraulic turbines, centrifugal pumps, spillways of dams, river channels etc and to study such phenomenon as the action of waves and tides on beaches, soil erosion, and transportation of sediment etc.

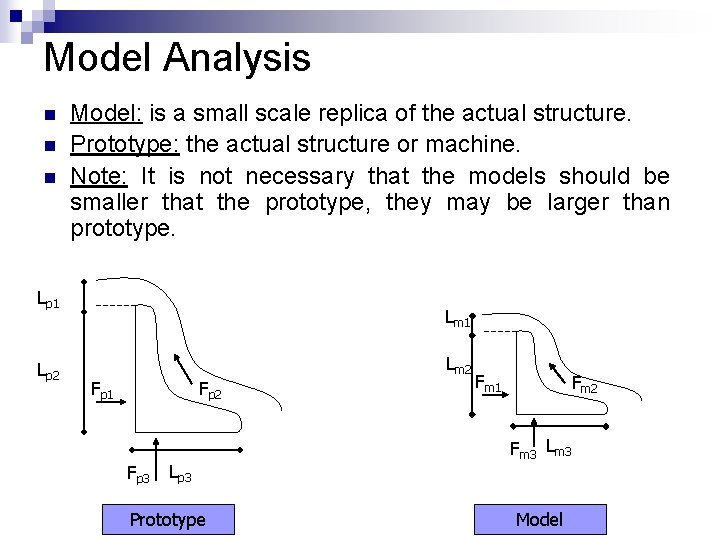
Model Analysis n n n Model: is a small scale replica of the actual structure. Prototype: the actual structure or machine. Note: It is not necessary that the models should be smaller that the prototype, they may be larger than prototype. Lp 1 Lp 2 Lm 1 Lm 2 Fp 1 Fp 2 Fp 3 Lp 3 Prototype Fm 1 Fm 2 Fm 3 Lm 3 Model

Model Analysis n Model Analysis is actually an experimental method of finding solutions of complex flow problems. n The followings are the advantages of the model analysis The performance of the hydraulic structure can be predicted in advance from its model. ¨ Using dimensional analysis, a relationship between the variables influencing a flow problem is obtained which help in conducting tests. ¨ The merits of alternative design can be predicted with the help of model analysis to adopt most economical, and safe design. ¨ n Note: Test performed on models can be utilized for obtaining, in advance, useful information about the performance of the prototype only if a complete similarity exits between the model and the prototype.

Similitude-Type of Similarities n Similitude: is defined as similarity between the model and prototype in every respect, which mean model and prototype have similar properties or model and prototype are completely similar. n Three types of similarities must exist between model and prototype. ¨ Geometric Similarity ¨ Kinematic Similarity ¨ Dynamic Similarity

Similitude-Type of Similarities n n Geometric Similarity: is the similarity of shape. It is said to exist between model and prototype if ratio of all the corresponding linear dimensions in the model and prototype are equal. E. g. Where: Lp, Bp and Dp are Length, Breadth, and diameter of prototype and Lm, Bm, Dm are Length, Breadth, and diameter of model. Lr= Scale ratio Note: Models are generally prepared with same scale ratios in every direction. Such a model is called true model. However, sometimes it is not possible to do so and different convenient scales are used in different directions. Such a models is call distorted model

Similitude-Type of Similarities n n Kinematic Similarity: is the similarity of motion. It is said to exist between model and prototype if ratio of velocities and acceleration at the corresponding points in the model and prototype are equal. E. g. Where: Vp 1& Vp 2 and ap 1 & ap 2 are velocity and accelerations at point 1 & 2 in prototype and Vm 1& Vm 2 and am 1 & am 2 are velocity and accelerations at point 1 & 2 in model. Vr and ar are the velocity ratio and acceleration ratio Note: Since velocity and acceleration are vector quantities, hence not only the ratio of magnitude of velocity and acceleration at the corresponding points in model and prototype should be same; but the direction of velocity and acceleration at the corresponding points in model and prototype should also be parallel.

Similitude-Type of Similarities n n Dynamic Similarity: is the similarity of forces. It is said to exist between model and prototype if ratio of forces at the corresponding points in the model and prototype are equal. E. g. Where: (Fi)p, (Fv)p and (Fg)p are inertia, viscous and gravitational forces in prototype and (Fi)m, (Fv)m and (Fg)m are inertia, viscous and gravitational forces in model. Fr is the Force ratio Note: The direction of forces at the corresponding points in model and prototype should also be parallel.

Types of forces encountered in fluid Phenomenon n Inertia Force, Fi: It is equal to product of mass and acceleration in the flowing fluid. n Viscous Force, Fv: It is equal to the product of shear stress due to viscosity and surface area of flow. n Gravity Force, Fg: It is equal to product of mass and acceleration due to gravity. n Pressure Force, Fp: it is equal to product of pressure intensity and cross-sectional area of flowing fluid. n Surface Tension Force, Fs: It is equal to product of surface tension and length of surface of flowing fluid. n Elastic Force, Fe: It is equal to product of elastic stress and area of flowing fluid.

Dimensionless Numbers n These are numbers which are obtained by dividing the inertia force by viscous force or gravity force or pressure force or surface tension force or elastic force. n As this is ratio of once force to other, it will be a dimensionless number. These are also called nondimensional parameters. n The following are most important dimensionless numbers. ¨ ¨ ¨ Reynold’s Number Froude’s Number Euler’s Number Weber’s Number Mach’s Number

Dimensionless Numbers n Reynold’s Number, Re: It is the ratio of inertia force to the viscous force of flowing fluid. n Froude’s Number, Re: It is the ratio of inertia force to the gravity force of flowing fluid.

Dimensionless Numbers n Eulers’s Number, Re: It is the ratio of inertia force to the pressure force of flowing fluid. n Weber’s Number, Re: It is the ratio of inertia force to the surface tension force of flowing fluid.

Dimensionless Numbers n Mach’s Number, Re: It is the ratio of inertia force to the elastic force of flowing fluid.

Lecture # 13

Model Laws or similarity Laws n n n We have already read that for dynamic similarity ratio of corresponding forces acting on prototype and model should be equal. i. e Force of inertial comes in play when sum of all other forces is not equal to zero which mean In case all the forces are equally important, the above two equations cannot be satisfied for model analysis

Model Laws or similarity Laws n However, for practical problems it is seen that one force is most significant compared to other and is called predominant force or most significant force. n Thus for practical problem only the most significant force is considered for dynamic similarity. Hence, models are designed on the basis of ratio of force, which is dominating in the phenomenon. n Finally the laws on which models are designed for dynamic similarity are called models laws or laws of similarity. The followings are these laws ¨ ¨ ¨ Reynold’s Model Law Froude’s Model Law Euler’s Model Law Weber’s Model Law mach’s Model Law

Reynold’s Model Law n n It is based on Reynold’s number and states that Reynold’s number for model must be equal to the Reynolds number for prototype. Reynolds Model Law is used in problems where viscous forces are dominant. These problems include: Pipe Flow ¨ Resistance experienced by submarines, airplanes, fully immersed bodies etc. ¨

Reynold’s Model Law n The Various Ratios for Reynolds’s Law are obtained as

Reynold’s Model Law Q. A pipe of diameter 1. 5 m is required to transport an oil of specific gravity 0. 90 and viscosity 3 x 10 -2 poise at the rate of 3000 litre/sec. Tests were conducted on a 15 cm diameter pipe using water at 20 o. C. Find the velocity and rate of flow in the model. Solution: Prototype Data: n n n n n Diameter, Dp= 1. 5 m Viscosity of fluid, μp= 3 x 10 -2 poise Discharge, Qp =3000 litre/sec Sp. Gr. , Sp=0. 9 Density of oil=ρp=0. 9 x 1000 =900 kg/m 3 Model Data: n n n Diameter, Dm=15 cm =0. 15 m Viscosity of water, μm =1 x 10 -2 poise Density of water, ρm=1000 kg/m 3 n Velocity of flow Vm=? Discharge Qm=?

Reynold’s Model Law n Q. A ship 300 m long moves in sea water, whose density is 1030 kg/m 3. A 1: 100 model of this ship is to be tested in a wind tunnel. The velocity of air in the wind tunnel around the model is 30 m/s and the resistance of the model is 60 N. Determine the velocity of ship in sea water and also the resistance of ship in sea water. The density of air is given as 1. 24 kg/m 3. Take the kinematic viscosity of sea water and air as 0. 012 stokes and 0. 018 stokes respectively. n n Solution: For Prototype n n n Length, Lp= 300 m Fluid = sea water Density of sea water, ρp= 1030 kg/m 3 Kinematic Viscosity, νp=0. 018 stokes =0. 018 x 10 -4 m 2/s Let Velocity of ship, Vp Resistance, Fp n For Model n n n n Scale ratio = Lp/Lm=100 Length, Lm= Lp/100 = 3 m Fluid = air Density of air, ρm= 1. 24 kg/m 3 Kinematic Viscosity, νm=0. 012 stokes =0. 012 x 10 -4 m 2/s Velocity of ship, Vm=30 m/s Resistance, Fm = 60 N

Reynold’s Model Law n For dynamic similarity between model and prototype, the Reynolds number for both of them should be equal.

Froude’s Model Law n n It is based on Froude’s number and states that Froude’s number for model must be equal to the Froude’s number for prototype. Froude’s Model Law is used in problems where gravity forces is only dominant to control flow in addition to inertia force. These problems include: Free surface flows such as flow over spillways, weirs, sluices, channels etc. ¨ Flow of jet from orifice or nozzle ¨ Waves on surface of fluid ¨ Motion of fluids with different viscosities over one another ¨

Froude’s Model Law n The Various Ratios for Reynolds’s Law are obtained as

Froude’s Model Law n Q. In the model test of a spillway the discharge and velocity of flow over the model were 2 m 3/s and 1. 5 m/s respectively. Calculate the velocity and discharge over the prototype which is 36 times the model size. n Solution: Given that n For Model n n Discharge over model, Qm=2 m 3/sec Velocity over model, Vm = 1. 5 m/sec Linear Scale ratio, Lr =36 For Prototype n n Discharge over prototype, Qp =? Velocity over prototype Vp=?

Numerical Problem: n n n Q. The characteristics of the spillway are to be studied by means of a geometrically similar model constructed to a scale of 1: 10. (i) If 28. 3 cumecs, is the maximum rate of flow in prototype, what will be the corresponding flow in model? (i) If 2. 4 m/sec, 50 mm and 3. 5 Nm are values of velocity at a point on the spillway, height of hydraulic jump and energy dissipated per second in model, what will be the corresponding velocity height of hydraulic jump and energy dissipation per second in prototype? Solution: Given that For Model n n n n Discharge over model, Qm=? Velocity over model, Vm = 2. 4 m/sec Height of hydraulic jump, Hm =50 mm Energy dissipation per second, Em =3. 5 Nm Linear Scale ratio, Lr =10 For Prototype n n Discharge over model, Qp=28. 3 m 3/sec Velocity over model, Vp =? Height of hydraulic jump, Hp =? Energy dissipation per second, Ep =?

Froude’s Model Law

Classification of Models n Undistorted or True Models: are those which are geometrically similar to prototype or in other words if the scale ratio for linear dimensions of the model and its prototype is same, the models is called undistorted model. The behavior of prototype can be easily predicted from the results of undistorted or true model. n Undistorted Models: A model is said to be distorted if it is not n geometrically similar to its prototype. For distorted models different scale ratios for linear dimension are used. For example, if for the river, both horizontal and vertical scale ratio are taken to be same, then depth of water in the model of river will be very small which may not be measured accurately. n The followings are the advantages of distorted models n n The vertical dimension of the model can be accurately measured The cost of the model can be reduced Turbulent flow in the model can be maintained Though there are some advantage of distorted models, however the results of such models cannot be directly transferred to prototype.

Classification of Models n Scale Ratios for Distorted Models

Distorted model n Q. The discharge through a weir is 1. 5 m 3/s. Find the discharge through the model of weir if the horizontal dimensions of the model=1/50 the horizontal dimension of prototype and vertical dimension of model =1/10 the vertical dimension of prototype.

Distorted model n Q. A river model is to be constructed to a vertical scale of 1: 50 and a horizontal of 1: 200. At the design flood discharge of 450 m 3/sec, the average width and depth of flow are 60 m and 4. 2 m respectively. Determine the corresponding discharge in model and check the Reynolds’ Number of the model flow.

Distorted model