Lecture 12 Controllability Observability Meiling CHEN Motivation 1

Lecture #12 Controllability & Observability Meiling CHEN
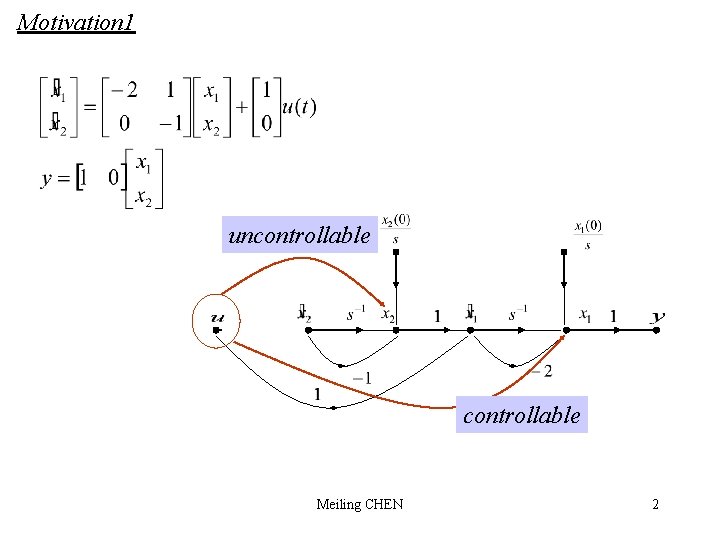
Motivation 1 uncontrollable Meiling CHEN 2
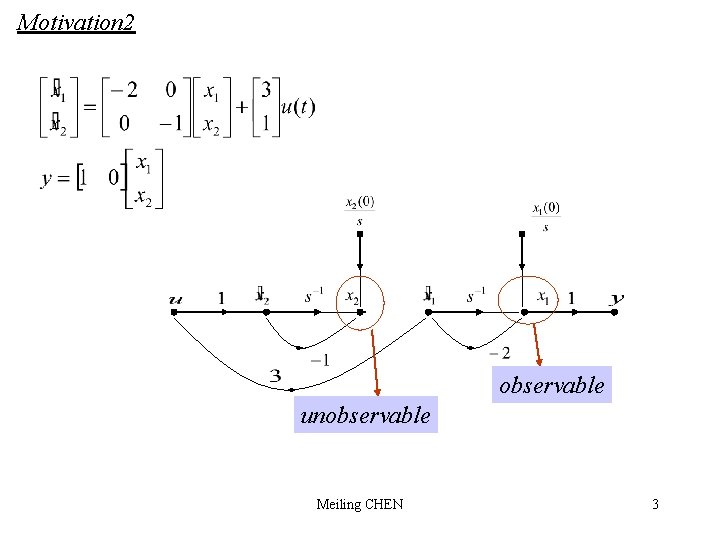
Motivation 2 observable unobservable Meiling CHEN 3

Definition A linear system is said to be completely controllable if, for all initial times and all initial states , there exists some input function (or sequence for discrete systems) that drives the state vector to any final state at some finite time. Definition A linear system is said to be completely observable if, for all initial times , the state vector can be determined from the output function (or sequence) , defined over a finite time. Meiling CHEN 4

Proof of controllability matrix Initial condition Meiling CHEN 5

Proof of observability matrix Inputs & outputs Meiling CHEN 6

Controllability matrix Observability matrix Then: (1) controllable (2) observable Meiling CHEN 7

Example 1 uncontrollable observable The rank of a matrix is defined by the number of linearly independent rows and/or the number of linearly independent columns Meiling CHEN 8
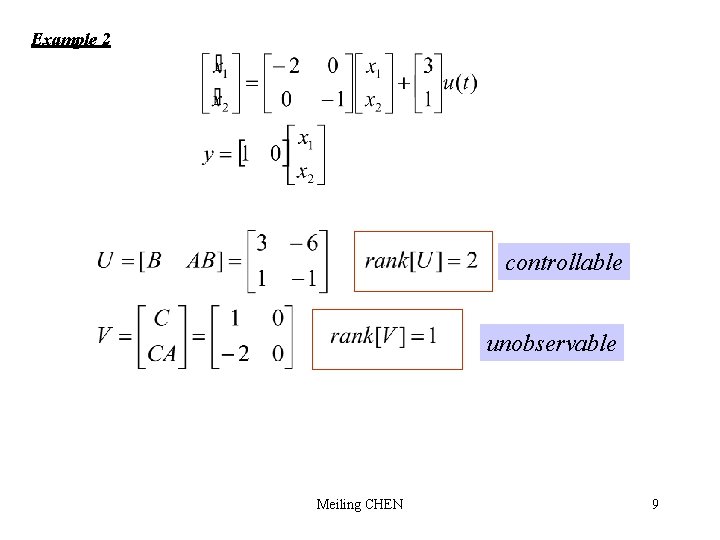
Example 2 controllable unobservable Meiling CHEN 9

Theorem III Controllable canonical form Controllable Theorem IV Observable canonical form Meiling CHEN Observable 10

example Controllable canonical form Observable canonical form Meiling CHEN 11
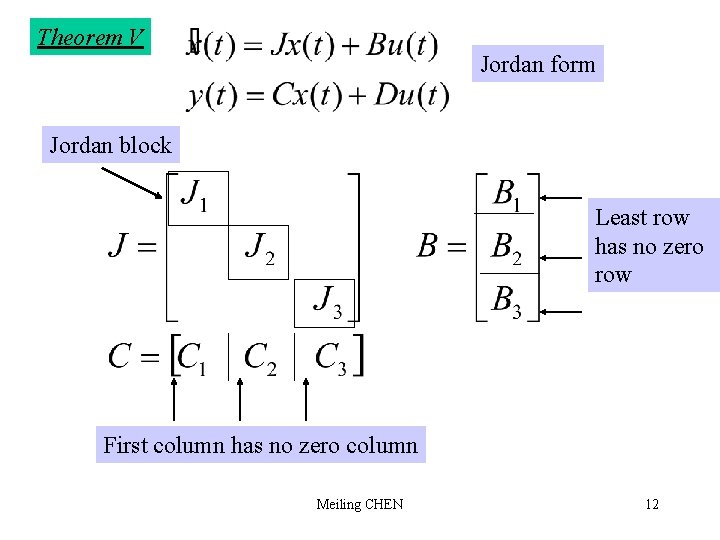
Theorem V Jordan form Jordan block Least row has no zero row First column has no zero column Meiling CHEN 12
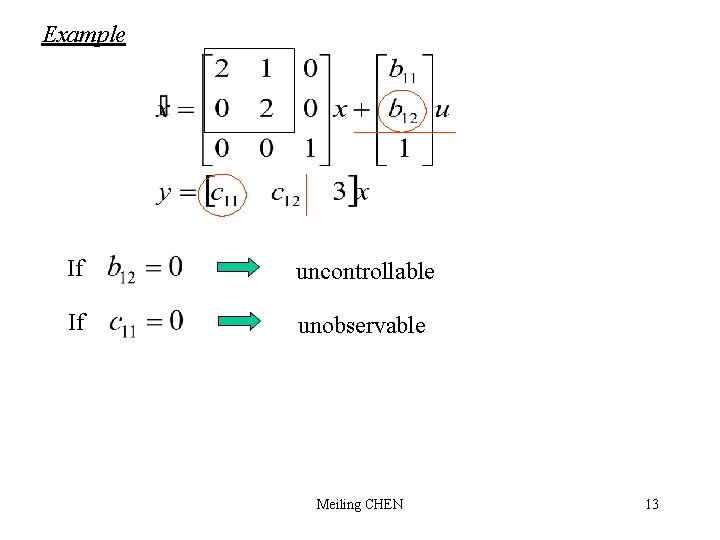
Example If uncontrollable If unobservable Meiling CHEN 13
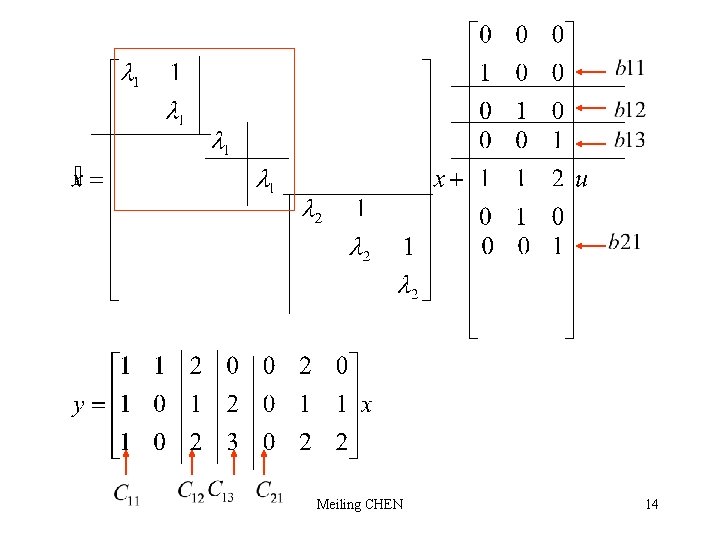
Meiling CHEN 14
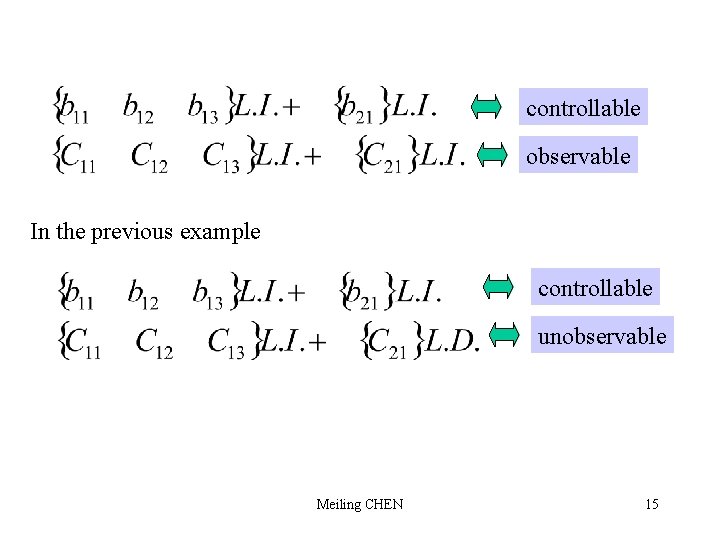
controllable observable In the previous example controllable unobservable Meiling CHEN 15
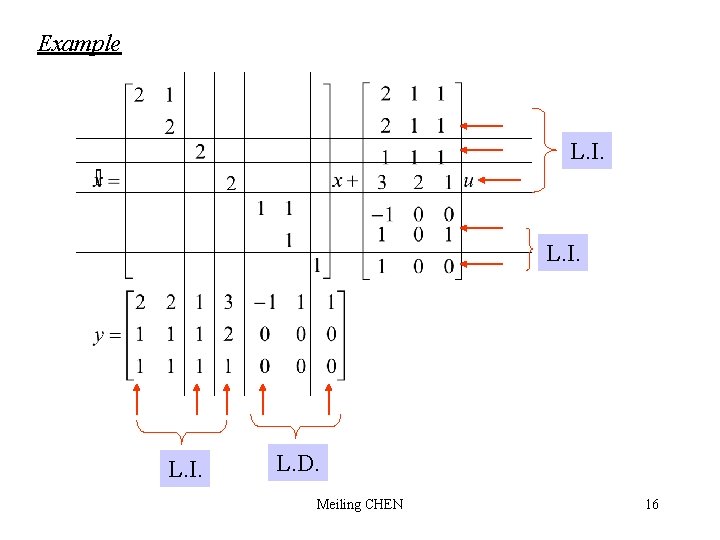
Example L. I. L. D. Meiling CHEN 16
- Slides: 16