Lecture 12 Collisions and Explosions l Momentum Examples

Lecture 12: Collisions and Explosions l Momentum Examples! è Problem Solving è Collisions (elastic & inelastic) è Explosions

Impulse and Momentum: quick review l Momentum-Impulse Theorem èF t I = pf - pi = p l For single object…. èIf F = 0, then momentum conserved ( p = 0) l For “system” of objects … èptotal p èInternal forces: forces between objects in system èExternal forces: all other forces èFext t = ptotal èif Fext = 0 , then total momentum conserved ( ptotal = 0) l Applications: Collisions & Explosions

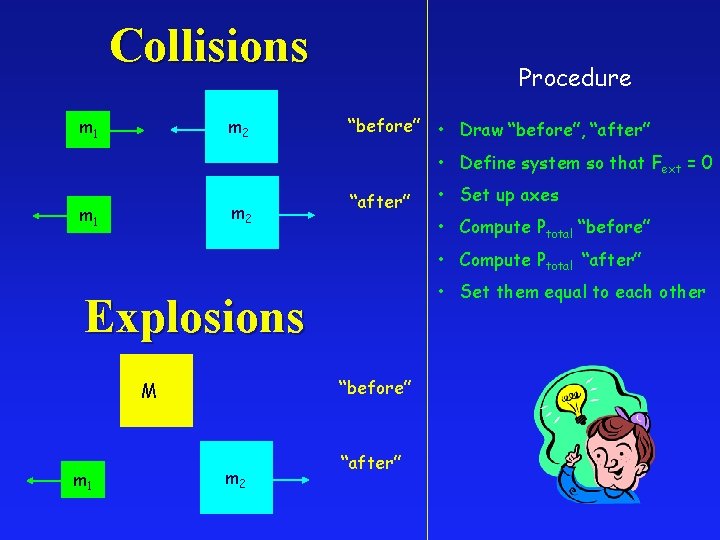
Collisions m 2 m 1 Procedure “before” • Draw “before”, “after” • Define system so that Fext = 0 m 2 m 1 “after” • Set up axes • Compute Ptotal “before” • Compute Ptotal “after” • Set them equal to each other Explosions “before” M m 1 m 2 “after”

Some Terminology • Elastic Collisions: collisions that conserve mechanical energy • Inelastic Collisions: collisions that do not conserve mechanical energy * Completely Inelastic Collisions: objects stick together

Collision Example l Two cars are approaching an intersection. The first car is 1520 kg and is moving east at 18 m/s; the second car is 1380 kg and is moving north at 16 m/s. The cars have a completely inelastic collision. What is their final velocity? y x Before: After:

Collision Example l Two cars are approaching an intersection. The first car is 1520 kg and is moving east at 18 m/s; the second car is 1380 kg and is moving north at 16 m/s. The cars have a completely inelastic collision. What is their final velocity? x-direction: pix = pfx (1520 kg)(18 m/s) + 0 = pfx y-direction: piy = pfy 0 + (1380 kg)(16 m/s) = pfy y x

Collision Example l Two cars are approaching an intersection. The first car is 1520 kg and is moving east at 18 m/s; the second car is 1380 kg and is moving north at 16 m/s. The cars have a completely inelastic collision. What is their final velocity? x-direction: (1520 kg)(18 m/s) + 0 = pfx (1520 kg)(18 m/s) = (1520 kg + 1380 kg) vfx y-direction: 0 + (1380 kg)(16 m/s) = pfy (1380 kg)(18 m/s) = (1520 kg + 1380 kg) vfy y x

Collision Example l Two cars are approaching an intersection. The first car is 1520 kg and is moving east at 18 m/s; the second car is 1380 kg and is moving north at 16 m/s. The cars have a completely inelastic collision. What is their final velocity? x-direction: vfx = 9. 43 m/s y-direction: vfy = 7. 61 m/s Vf = 12. 1 m/s at 51º east of north y x

Explosion Example l A ball has a mass of 3 kg. It explodes into three equal masses, shooting a 1 kg piece in the positive y direction with speed v and another 1 kg piece in the positive x direction with speed v. What is the speed and direction of the remaining 1 kg piece? y x Before: After:

Explosion Example l A ball has a mass of 3 kg. It explodes into three equal masses, shooting a 1 kg piece in the positive y direction with speed v and another 1 kg piece in the positive x direction with speed v. What is the speed and direction of the remaining 1 kg piece? x-direction: pix = pfx 0 + 0 = 0 + (1 kg) vfx y-direction: piy = pfy 0 + 0 = (1 kg) v + 0 + (1 kg) vfy y x

Explosion Example l A ball has a mass of 3 kg. It explodes into three equal masses, shooting a 1 kg piece in the positive y direction with speed v and another 1 kg piece in the positive x direction with speed v. What is the speed and direction of the remaining 1 kg piece? x-direction: vfx = -v y-direction: vfy = -v Vf = v 2 at 45º below the –x axis y x

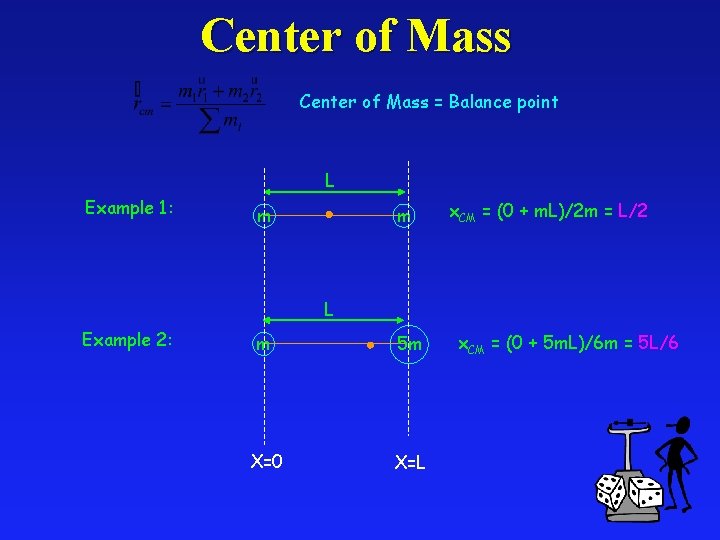
Center of Mass = Balance point L Example 1: m m x. CM = (0 + m. L)/2 m = L/2 L Example 2: m 5 m X=0 X=L x. CM = (0 + 5 m. L)/6 m = 5 L/6

Summary • Collisions and Explosions • Draw “before”, “after” • Define system so that Fext = 0 • Set up axes • Compute ptotal “before” • Compute ptotal “after” • Set them equal to each other • Center of Mass (Balance Point)