Lecture 11 II Iterative approaches for solving linear

Lecture 11 -II Iterative approaches for solving linear systems ØSuccessive over-relaxation ØPost-nonlinear system ØPartial pivoting Numerical method 1

Derivation of Successive overrelaxation Numerical method 2

Successive over-relaxation method D=diag(A)); U=triu(A)-D; L=A-triu(A); R=D+w*L; T=inv(R)*((1 -w)*D-w*U); c=w*inv(R)*b; Numerical method 3

Successive over-relaxation method A, b it_xor. m x A=[10 -1 2 0; -1 11 -1 3; 2 -1 10 -1; 0 3 -1 8]; b=[6 25 -11 15]'; inv(A)*b Numerical method 4

>> it_xor(A, b) It takes 17 iterations to converge ans = 1. 0000300255 2. 0000357295 -1. 0000163021 0. 9999724547 Numerical method 5

Variant successive overrelaxation Numerical method 6

Variant Successive overrelaxation D=diag(A)); U=triu(A)-D; L=A-triu(A); R=w*D+D+L; T=inv(R)*(w*D-U); c=inv(R)*b; Numerical method 7

Variant Successive overrelaxation method A, b it_vxor. m x A=[10 -1 2 0; -1 11 -1 3; 2 -1 10 -1; 0 3 -1 8]; b=[6 25 -11 15]'; inv(A)*b Numerical method 8

>> it_vxor(A, b, w) It takes 17 iterations to converge ans = 1. 0000300255 2. 0000357295 -1. 0000163021 0. 9999724547 Numerical method 9

w=0 >> it_vxor(A, b, 0) It takes 10 iterations to converge ans = 0. 999998681 1. 9999985957 -0. 999997639 1. 000005561 Numerical method 10

Large w >> it_vxor(A, b, 3) It takes 90 iterations to converge ans = 0. 99999998371358 1. 99999997234472 -0. 99999998858309 1. 00000003116601 Numerical method 11

Post-Nonlinear System n n n Ax=b, A=rand(100, 100), b=rand(100, 1) f(Ax)=b, where f is an arbitrary onedimensional nonlinear function Given A, b find f and x Numerical method 12

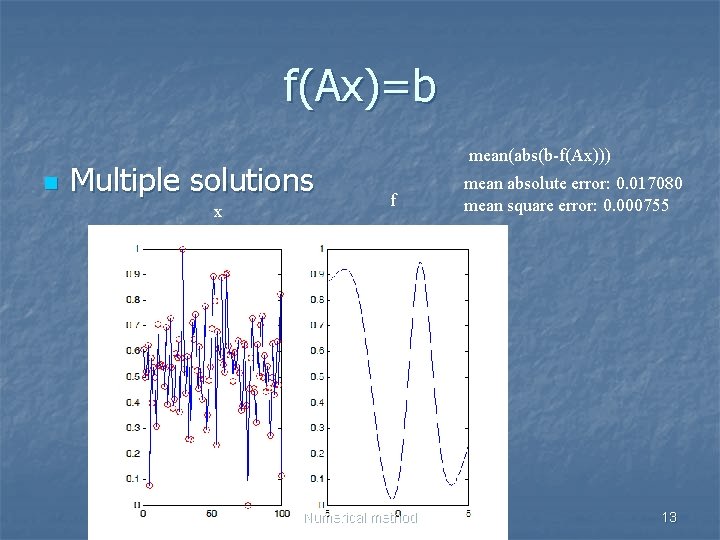
f(Ax)=b n Multiple solutions x mean(abs(b-f(Ax))) f Numerical method mean absolute error: 0. 017080 mean square error: 0. 000755 13

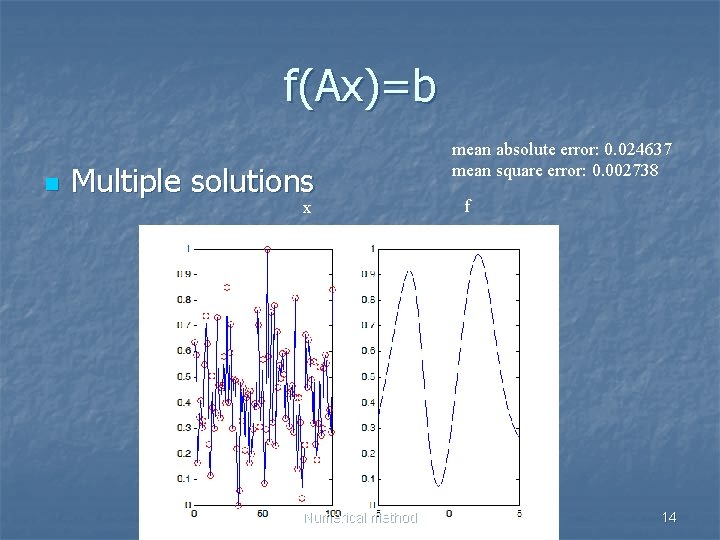
f(Ax)=b n Multiple solutions x Numerical method mean absolute error: 0. 024637 mean square error: 0. 002738 f 14

Matrix inversion n n Solve Gx=f Example Gf. zip n >> load Gf. mat; >> inv(G); Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 4. 206041 e-017. Numerical method 15

rank ss=cputime; for i=1: 1000 rank(G); end ss 2=cputime; fprintf('cputime: rank %f n', ss 2 -ss); cputime: rank 1. 703125 Numerical method 16

rank ss=cputime; for i=1: 50000 rank(G); end ss 2=cputime; fprintf('cputime: rank %f n', ss 2 -ss); cputime: rank 82. 546875 Numerical method 17

pinv ss=cputime; for i=1: 1000 pinv(G); end ss 2=cputime; fprintf('cputime: pinv %f n', ss 2 -ss); cputime: pinv 7. 062500 Numerical method 18

Inverse of submatrix ss=cputime; for i=1: 50000 inv(G(1: 61, 1: 61)); end ss 2=cputime; fprintf('cputime: pinv %f n', ss 2 -ss); cputime: inv of submatrix 28. 937500 Time reduced from 50*7. 06 to 28. 93 sec Numerical method 19

Partial pivoting n Maximal column pivoting The pivot or pivot element is the element of a matrix, which is selected first by an algorithm (e. g. Gaussian elimination, Quicksort, Simplex algorithm), to do certain calculations with the matrix Numerical method 20

A=[10. ^-16 59. 17; 5. 29 -6. 13]; b=[59. 17 46. 78]'; B=[A b]; B=f. Gauss(B) f. Gauss. m B x=backward(B) backward. m 0. 0 1. 0000 Numerical method ans = 10. 0019 1. 0000 21

B= 10. ^-16 59. 1400 59. 1700 5. 2900 -6. 1300 46. 7800 Find Exchange row 1 and row 2 temp=B(1, : ); B(1, : )=B(2, : ); B(2, : )=temp; Numerical method 22

B= 5. 2900 -6. 1300 46. 7800 10. ^-16 59. 1400 59. 1700 U=f. Gauss(B); x=backward(U) x= 10. 0019 1. 0000 Numerical method 23

A=[30. 00 591400; 5. 29 -6. 13]; b=[591700 46. 78]'; B=[A b]; Numerical method 24

Scaled partial pivoting Exchange row i and row p Numerical method 25

A= 2. 1100 -4. 2100 0. 9210 4. 0100 10. 2000 -1. 1200 1. 0900 0. 9870 0. 8320 >> s=max(abs(A'))' s= 4. 2100 10. 2000 1. 0900 Determine the first pivot by [v p]=max(A(: , 1). /s); p= 3 Numerical method 26

Scaled partial pivoting Function [B, pr]=pss(A, b) n=length(b); B=[A b]; pr=[]; s=max(abs(A'))' Pr=1: n; for i= 1: n A. B. C. D. Find the ith pivot row and set it to p Exchange pr(i) and pr(p) Exchange row i and row p of matrix B For each row j > i 1) 2) Set d to the ratio B(j, i) / B(i, i) Set B(j, : ) to B(j, : )-d*B(i, : ) Return B and pr Numerical method 27

Example A=[2. 11 -4. 21. 921; 4. 01 10. 2 -1. 12; 1. 09. 987. 832]; b=[2. 01 -3. 09 4. 21]'; spp. m [B, pr]=spp(A, b) B= 1. 0900 0. 9870 0. 8320 4. 2100 0 -6. 1206 -0. 6896 -6. 1396 0 0. 0000 -4. 9209 -25. 1675 pr = 3 1 Numerical method 2 28

Example A=[1. 19 2. 11 -100 1; 14. 2 -0. 122 12. 2 -1; 0 100 -99. 9 1; 15. 3 0. 110 -13. 1 -1]; b=[1. 12 3. 44 2. 15 4. 16]'; [B, pr]=spp(A, b); x=backward(B); Numerical method x= 0. 1768 0. 0127 -0. 0207 -1. 1826 29

Exercise n n Implement the scaled partial pivoting method to improve the forward Gauss elimination method. Verify your matlab codes by two examples Numerical method 30

Avoid row swapping n n Row swapping results in time consuming No row swapping Use a vector v to emulate row swapping n Swap elements in v instead of swapping rows in B n n How to revise spp. m to avoid row swapping ? Numerical method 31