Lecture 11 Geometry of the Ellipse 25 February

Lecture 11: Geometry of the Ellipse 25 February 2008 GISC-3325

Class Update • • Next exam 12 March 2008 Labs 1 -4 due today! Homework 2 due 3 March 2008 Will have exams graded by next Monday – Will post solutions to class web page

Note on orthometric heights • Orthometric height differences are provided by leveling ONLY when there is parallelism between equipotential surfaces. – Over short distances this may be the case. • To account for non-parallelism we use geopotential numbers in computations. • In general, geopotential surfaces are NOT parallel in a N-S direction but are E-W
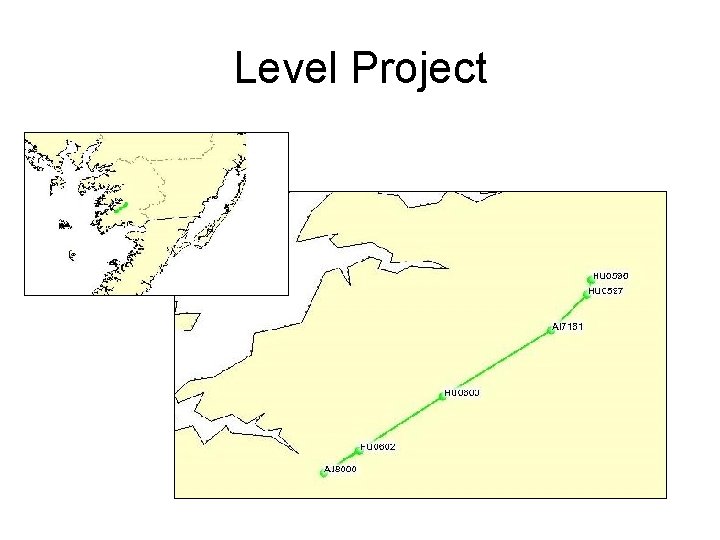
Level Project
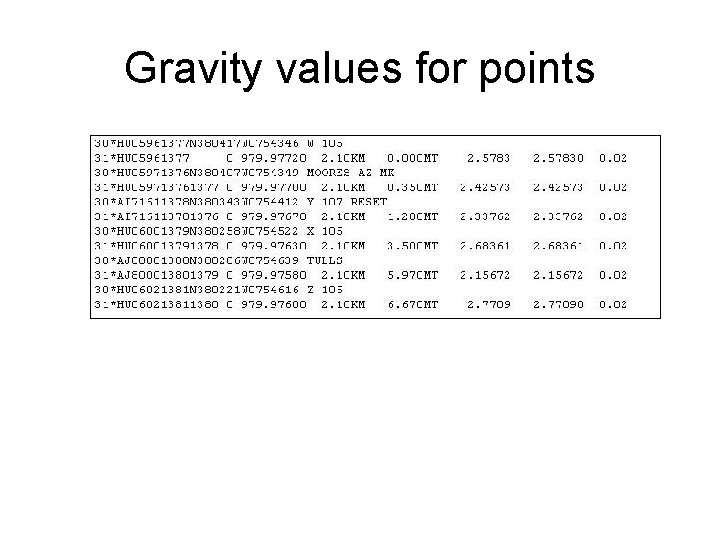
Gravity values for points

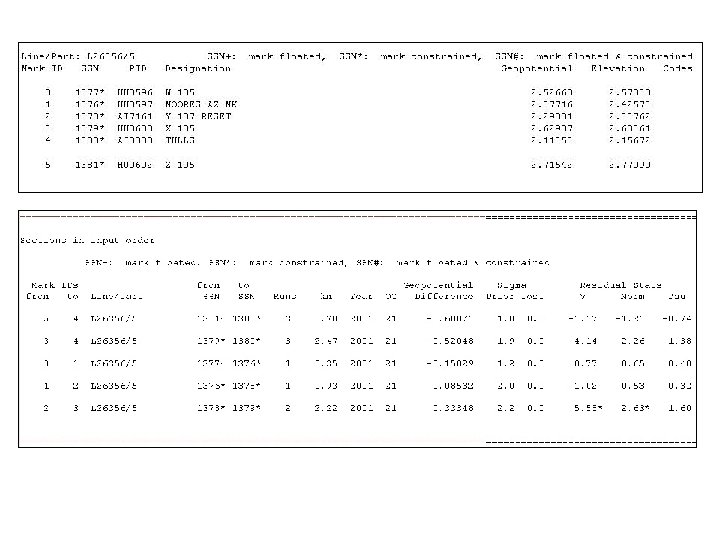
Helmert Orthometric Heights


Geometry of the Ellipsoid • Ellipsoid of revolution is formed by rotating a meridian ellipse about its minor axis thereby forming a 3 -D solid, the ellipsoid. • Modern models are chosen on the basis of their fit to the geoid. – Not always the case!

Parameters • • • a = semi-major axis length b = semi-minor axis length f = flattening = (a-b)/a e = first eccentricity = √((a 2 -b 2)/a 2) e’ = second eccentricity = √((a 2 -b 2)/b 2)
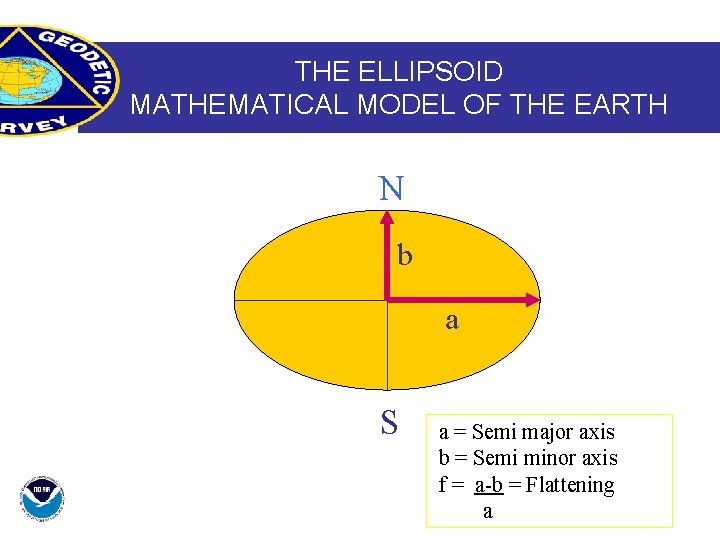
THE ELLIPSOID MATHEMATICAL MODEL OF THE EARTH N b a S a = Semi major axis b = Semi minor axis f = a-b = Flattening a

THE GEOID AND TWO ELLIPSOIDS CLARKE 1866 GRS 80 -WGS 84 Earth Mass Center Approximately 236 meters GEOID

NAD 83 and ITRF / WGS 84 NAD 83 ITRF / WGS 84 Earth Mass Center 2. 2 m (3 -D) d. X, d. Y, d. Z GEOID

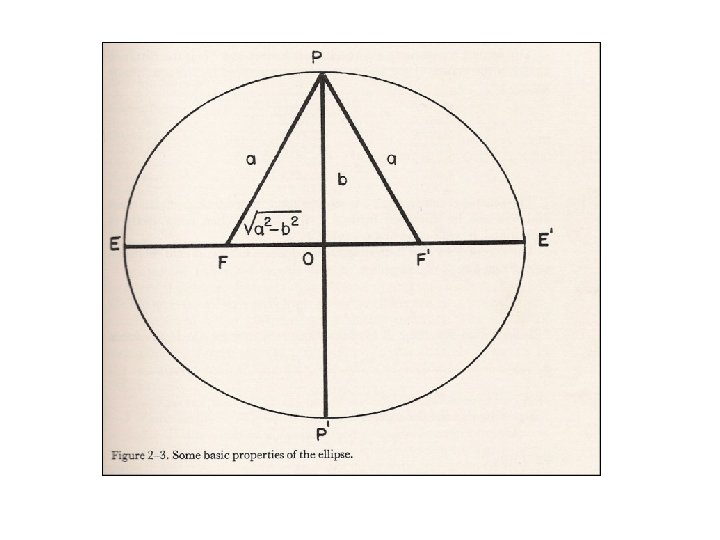
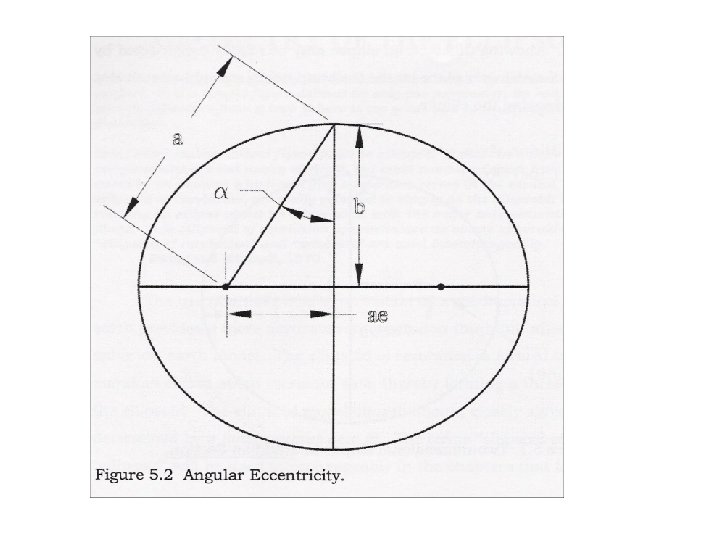


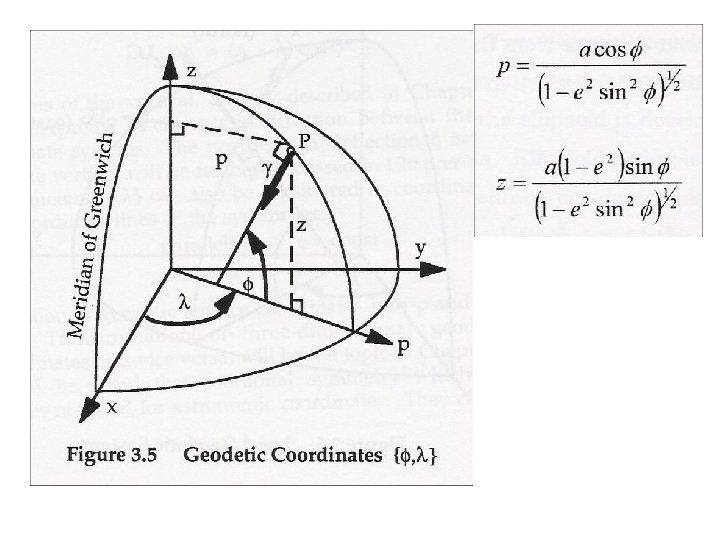
Geodetic latitude Geocentric latitude Parametric latitude Unlike the sphere, the ellipsoid does not possess a constant radius of curvature.




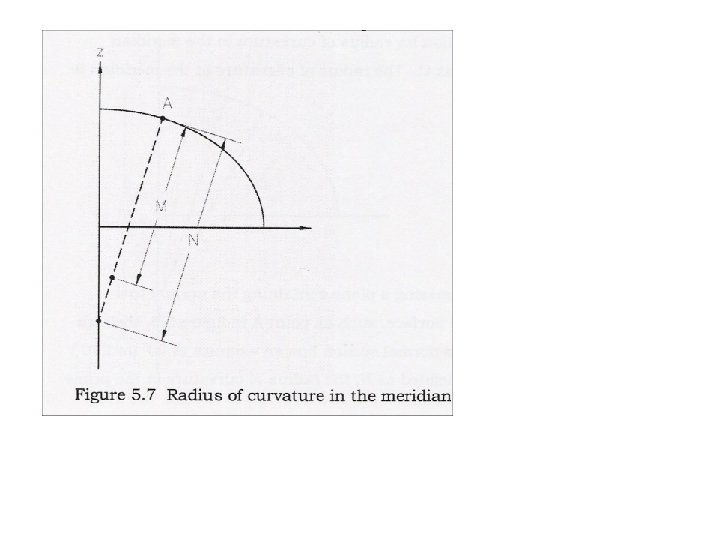
Radius of Curvature of the Prime Vertical

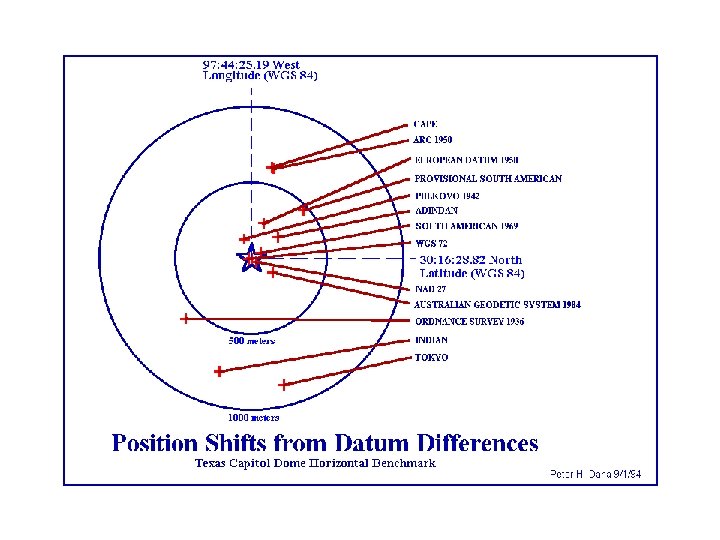
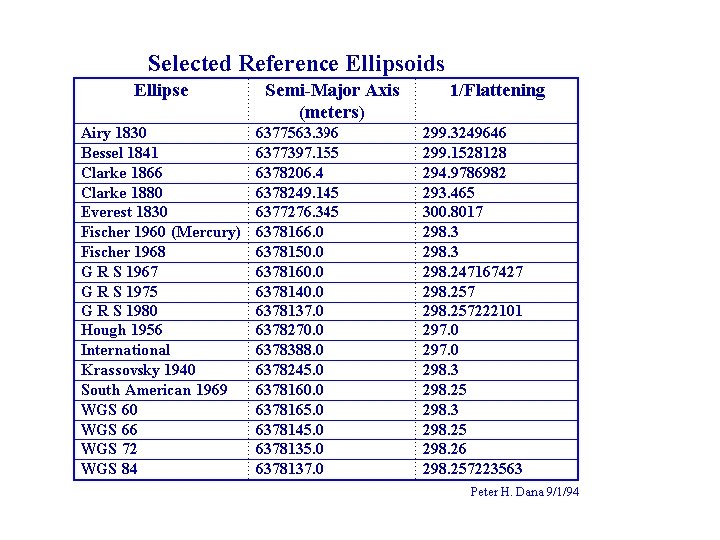
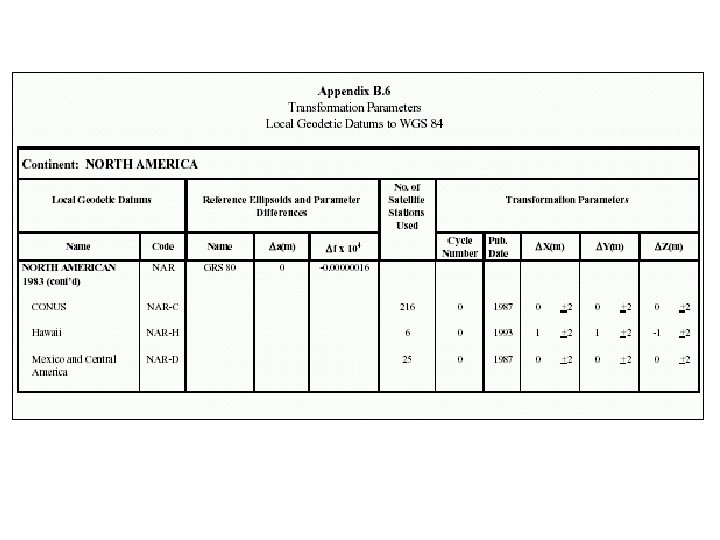
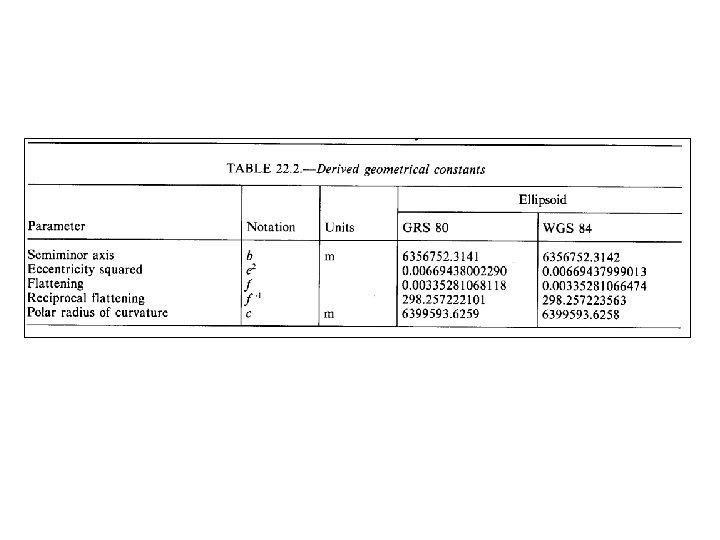
- Slides: 29