Lecture 11 ContextFree Grammar Definition A contextfree grammar

Lecture 11 Context-Free Grammar

Definition • A context-free grammar (CFG) G is a quadruple (V, Σ, R, S) where • V: a set of non-terminal symbols • Σ: a set of terminals (V ∩ Σ = Ǿ) • R: a set of rules (R: V → (V U Σ)*) • S: a start symbol.

How do we use rules? • If A → B, then x. Ay derivates x. By and we say that • If s ··· t, then we write s * t. • A string x in Σ* is generated by G=(V, Σ, R, S) if S * x. • L(G) = { x in Σ* | S * x}.

Example • • G = ({S}, {0, 1}. {S → 0 S 1 | ε }, S) ε in L(G) because S ε. 01 in L(G) because S 0 S 1 01. 0011 in L(G) because S 0 S 1 00 S 11 0011. n n • 0 1 in L(G) because S * 0 1. n n • L(G) = {0 1 | n > 0}

Context-Free Language (CFL) • A language L is context-free if there exists a CFG G such that L = L(G).

Theorem • For every regular set, there exists a CFG G such that L=L(G). Proof. Let L=L(M) for a DFA M=(Q, Σ, δ, s, F). Construct a CFG G=(V, Σ, R, S) as follows. V = Q, Σ = Σ, R = { q → ap | δ(q, a) = p } U { f → ε | f in F}, S = s. x 1 s xn q 1 S f=qn x q x x q ··· x 1…xnf x 1…xn 1 1 1 2 2

x in L(M) There is a path associated with x from initial state to a final state. S *x Therefore, L(M) = L(G).

Corollary • Every regular language is a CFL. • The class of regular languages is a proper subclass of CFLs. CFL Regular Why, proper?

Regular Grammar • Regular grammar is a CFG (V, Σ, R, S) such that every rule is in form V→ Σ*(V+ε) • Example G = ({S, A}, {0, 1}, {S → 1 A, A → 00}, S) • Remark: Every regular language can be generated by a regular grammar.

Theorem • Every regular grammar generates a regular language. Proof. Consider a regular grammar G=(V, Σ, R, S). Construct a string-labeled digraph with vertex set V U {f} as follows: For each rule A → x. B, x in Σ* and B in V, x draw an edge A → B. x For each rule A → x, x in Σ*, draw an edge A → f

Example 0 S G = ({S, A}, {0, 1}, {S→ 0 S | 10 A, A→ 00}, S) 10 A 00 f This string-labeled digraph with initial state S and a final state f is a state diagram of an NFA M. S * x in Σ* There is a path associated with x from S to f in M. Therefore, L(G) = L(M).

Corollary A language L is regular if and only if L can be generated by a regular grammar.

Right-Linear and Left-Linear • The regular grammar is also called a rightlinear grammar. • A grammar G=(V, Σ, R, S) is left-linear if every rule is in form V → (V+ε)Σ*. (e. g. , ({S, A}, {0, 1}, {S→A 01, A→ 10}, S) Remark: Every language generated from a left-linear grammar is regular. Why?

Why? • For left-linear grammar G = (V, Σ, R, S), R R construct G = (V, Σ, R , S) where R R R = {A→W | A→W in R}. R R • G is right-linear. Hence, L(G ) is regular. R R • Therefore, L(G) = L(G ) is regular.

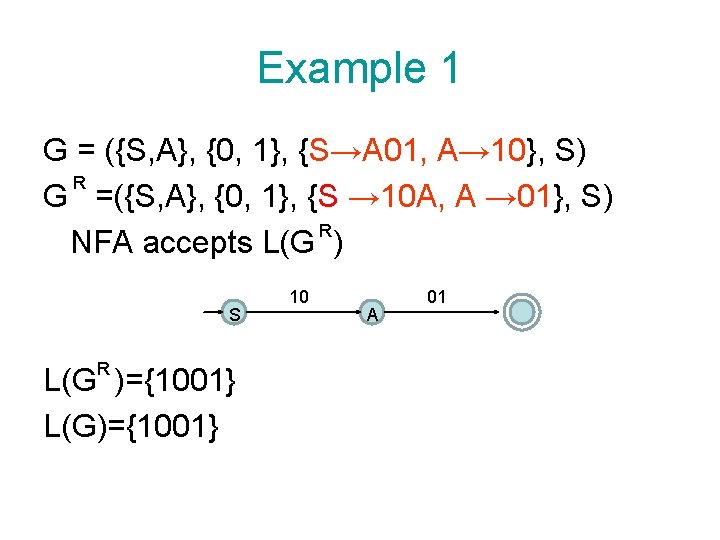
Example 1 G = ({S, A}, {0, 1}, {S→A 01, A→ 10}, S) R G =({S, A}, {0, 1}, {S → 10 A, A → 01}, S) R NFA accepts L(G ) S R L(G )={1001} L(G)={1001} 10 A 01

Example 2 L(G) = 0*1 R L(G ) = 10* NFA accepts 10* S R 1 A 0 G = ({S, A}, {0, 1}, {S → 1 A, A → 0 A|ε}, S) G = ({S, A}, {0, 1}, {S →A 1, A →A 0|ε}, S)