Lecture 11 b Polyatomic ideal gas Model translation

Lecture 11 b Polyatomic ideal gas Model - translation, rotation, vibration Rotational partition function Vibrational partition function - harmonic oscillator Thermodynamic functions Problems

Single polyatomic molecule Translational, rotational, vibrational and electronic energies additive qt - evaluated last lecture qr and qv - will evaluated today Typically with De - binding energy

Translation Consider a single diatomic molecule is the box Translation: M =m 1+m 2

Rotation energies: Degeneracy �r is the rotational temperature

Rotation - continuation Unless temperature is very low: If two atoms are the same we overcounted states by �- symmetry number

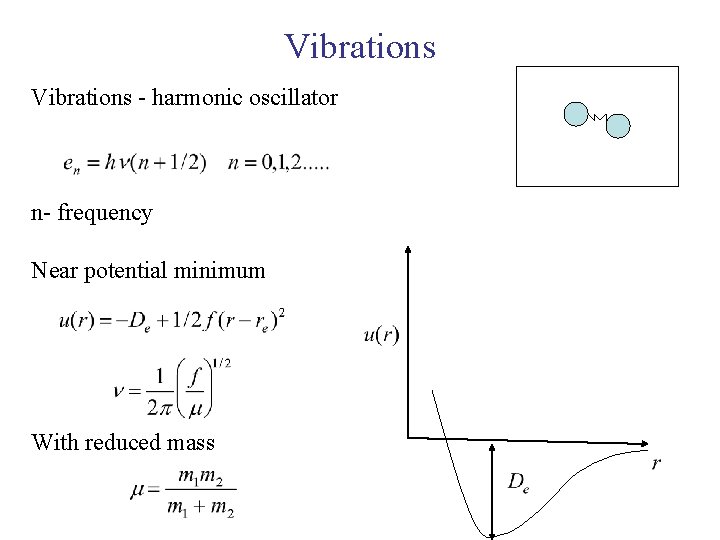
Vibrations - harmonic oscillator n- frequency Near potential minimum With reduced mass

Vibrations - continuation Partition function Vibrational temperature

Ideal Gases Molecular Energies • The schematic below gives an indication of the relative spacing between energy levels for the various energies electronic vibrational rotational translational

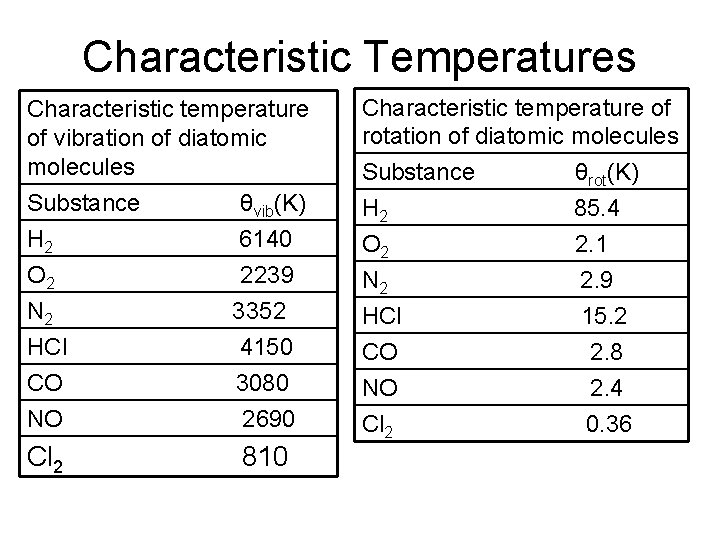
Characteristic Temperatures Characteristic temperature of vibration of diatomic molecules Substance θvib(K) H 2 O 2 N 2 HCl CO NO 6140 2239 3352 4150 3080 2690 Cl 2 810 Characteristic temperature of rotation of diatomic molecules Substance θrot(K) H 2 85. 4 O 2 N 2 HCl CO NO Cl 2 2. 1 2. 9 15. 2 2. 8 2. 4 0. 36

Partition function Q and free energy F translation vibrations rotation electronic

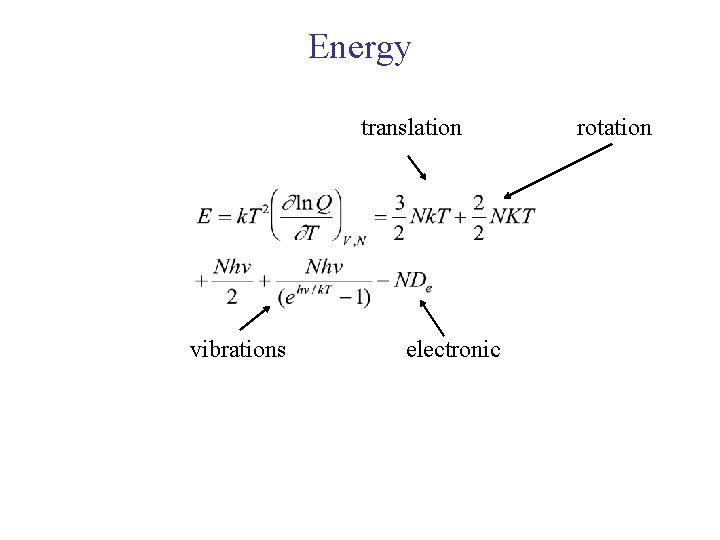
Energy translation vibrations electronic rotation

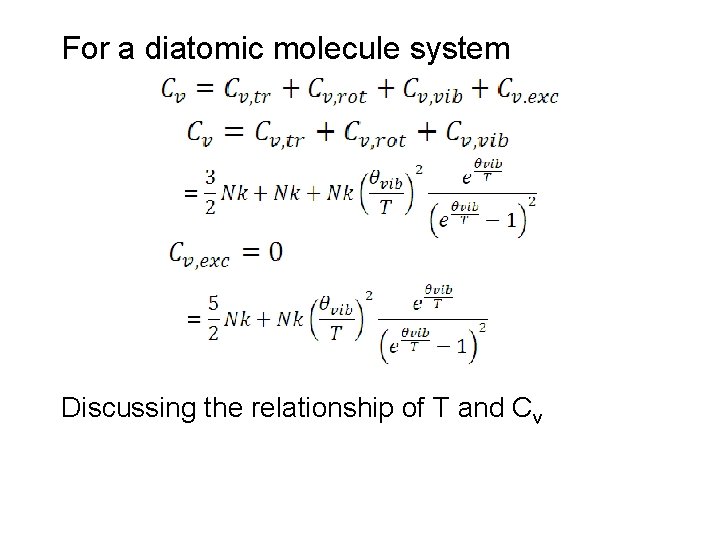
For a diatomic molecule system Discussing the relationship of T and Cv

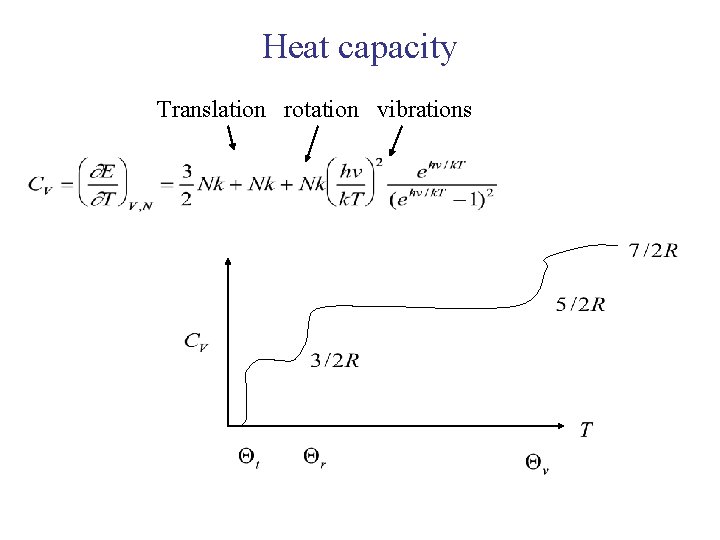
Heat capacity Translation rotation vibrations

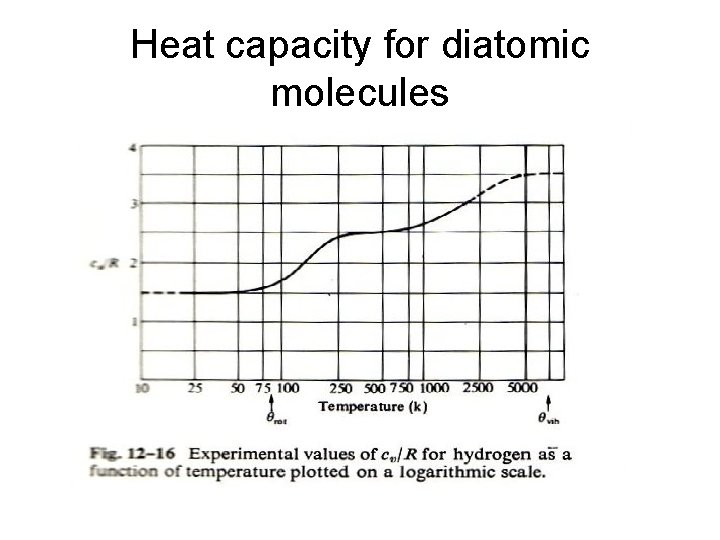
Heat capacity for diatomic molecules

Chemical potential