LECTURE 11 12 Course Design of Systems Structural

  • Slides: 14
Download presentation
LECTURE 11 -12. Course: “Design of Systems: Structural Approach” Dept. “Communication Networks &Systems”, Faculty

LECTURE 11 -12. Course: “Design of Systems: Structural Approach” Dept. “Communication Networks &Systems”, Faculty of Radioengineering & Cybernetics Moscow Inst. of Physics and Technology (University) Mark Sh. Levin Inst. for Information Transmission Problems, RAS Email: mslevin@acm. org / mslevin@iitp. ru PLAN: 1. Framework of multicriteria decision making 2. Partitioning the procedure of multicriteria decision making 3. Numerical examples: *partitioning of initial problem *aggregation of results 4. Mapping Sept. 25, 2004

Framework of multicriteria decision making & its partitioning (parallelization) DECISION MAKER DM ALTERNATIVES CRITERIA

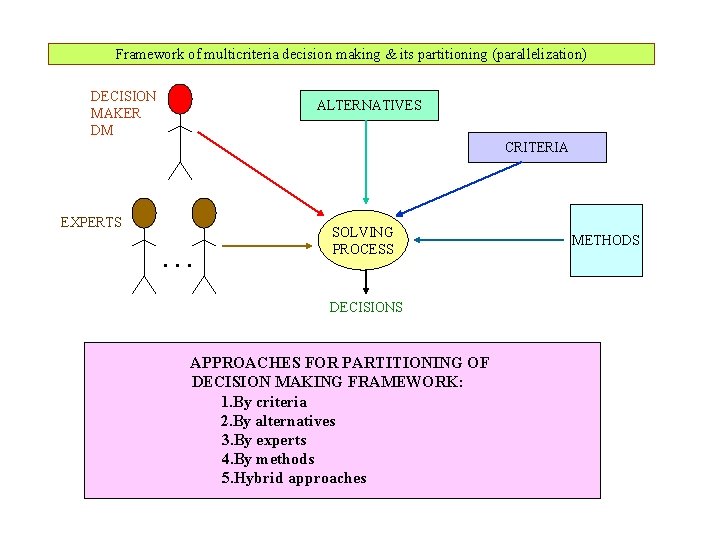
Framework of multicriteria decision making & its partitioning (parallelization) DECISION MAKER DM ALTERNATIVES CRITERIA EXPERTS . . . SOLVING PROCESS DECISIONS APPROACHES FOR PARTITIONING OF DECISION MAKING FRAMEWORK: 1. By criteria 2. By alternatives 3. By experts 4. By methods 5. Hybrid approaches METHODS

Parallel Processing Scheme DATA (VERSION 1) SOLVING PROCESS . . . INITIAL DATA PARTITIONING

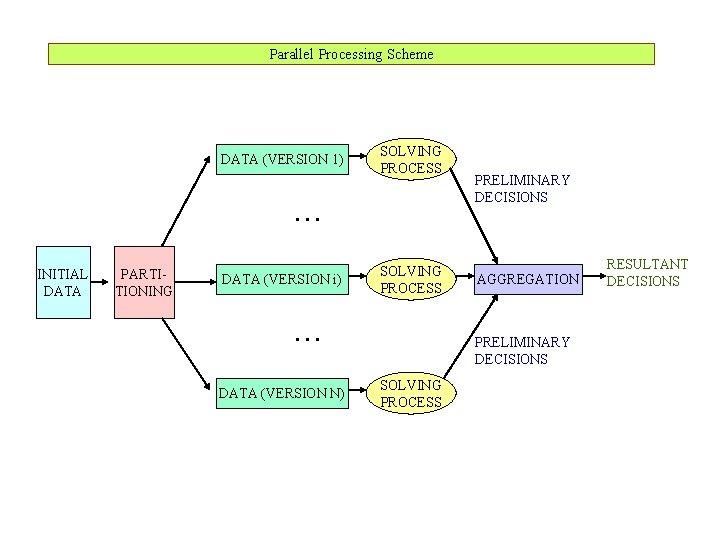
Parallel Processing Scheme DATA (VERSION 1) SOLVING PROCESS . . . INITIAL DATA PARTITIONING DATA (VERSION i) SOLVING PROCESS . . . DATA (VERSION N) PRELIMINARY DECISIONS AGGREGATION PRELIMINARY DECISIONS SOLVING PROCESS RESULTANT DECISIONS

Example: Partitioning by criteria groups A 1 A 2 A 3 A 4 A

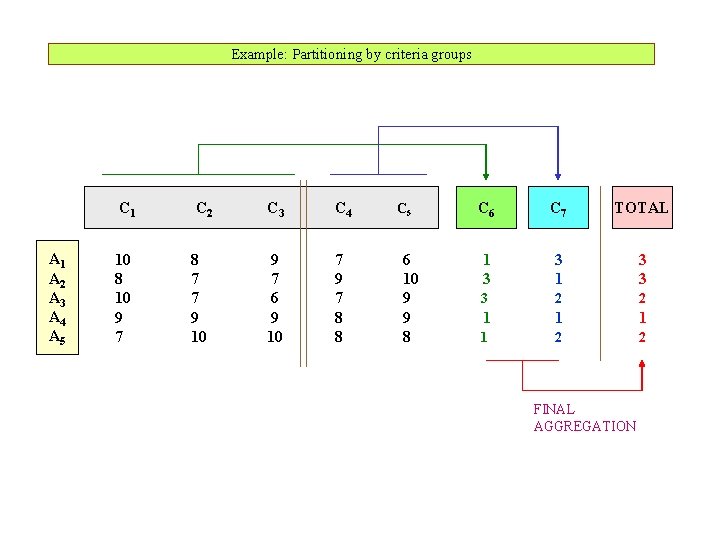
Example: Partitioning by criteria groups A 1 A 2 A 3 A 4 A 5 C 1 C 2 C 3 C 4 10 8 10 9 7 8 7 7 9 10 9 7 6 9 10 7 9 7 8 8 C 5 6 10 9 9 8 C 6 C 7 TOTAL 1 3 3 3 2 2 1 1 2 2 FINAL AGGREGATION

Example: Partitioning by alternative groups PRELIMINARY STAGE FINAL STAGE C 1 A 2 A

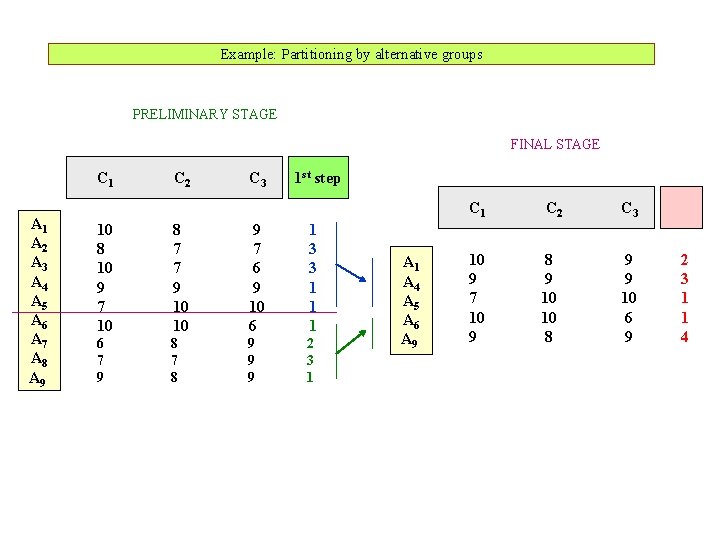
Example: Partitioning by alternative groups PRELIMINARY STAGE FINAL STAGE C 1 A 2 A 3 A 4 A 5 A 6 A 7 A 8 A 9 C 2 C 3 1 st step 10 8 10 9 7 10 8 7 7 9 10 10 9 7 6 9 10 6 1 3 3 1 1 1 6 7 9 8 7 8 9 9 9 2 3 1 A 4 A 5 A 6 A 9 C 1 C 2 C 3 10 9 7 10 9 8 9 10 10 8 9 9 10 6 9 2 3 1 1 4

Example: Joint partitioning by criteria groups & alternative groups C 1 A 2 A

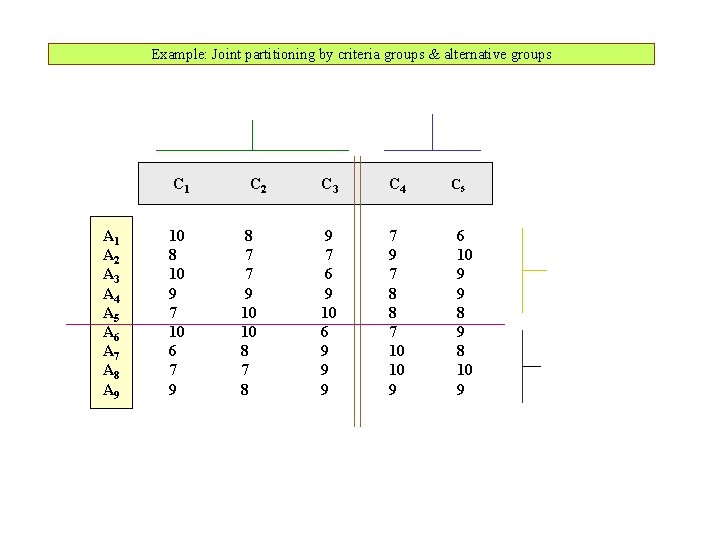
Example: Joint partitioning by criteria groups & alternative groups C 1 A 2 A 3 A 4 A 5 A 6 A 7 A 8 A 9 10 8 10 9 7 10 6 7 9 C 2 8 7 7 9 10 10 8 7 8 C 3 C 4 9 7 6 9 10 6 9 9 9 7 8 8 7 10 10 9 C 5 6 10 9 9 8 10 9

Possible schemes for joint partitioning by criteria groups & alternative groups C 1 A

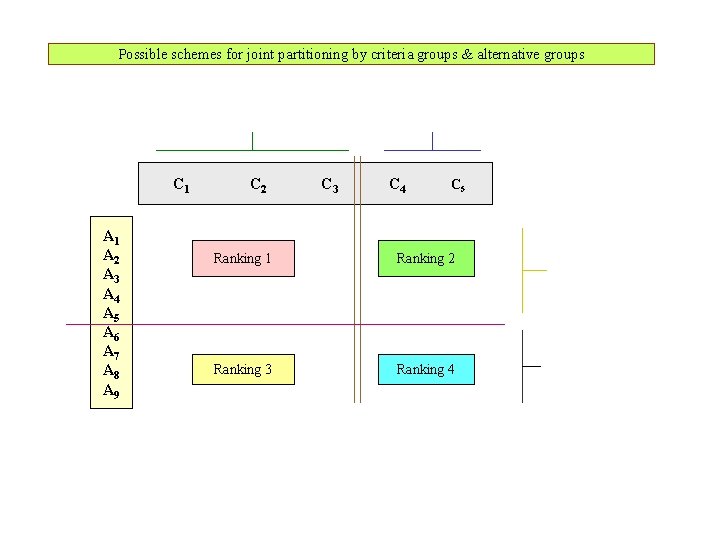
Possible schemes for joint partitioning by criteria groups & alternative groups C 1 A 2 A 3 A 4 A 5 A 6 A 7 A 8 A 9 C 2 C 3 C 4 C 5 Ranking 1 Ranking 2 Ranking 3 Ranking 4

Possible schemes for joint partitioning by criteria groups & alternative groups Ranking 1 SCHEME

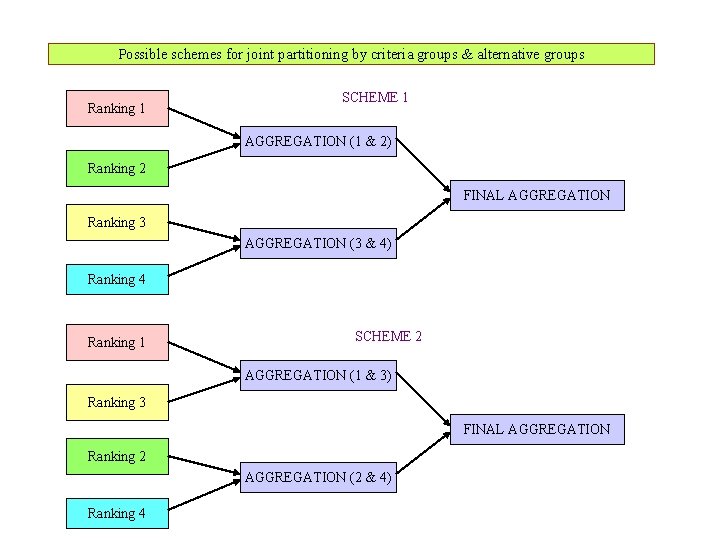
Possible schemes for joint partitioning by criteria groups & alternative groups Ranking 1 SCHEME 1 AGGREGATION (1 & 2) Ranking 2 FINAL AGGREGATION Ranking 3 AGGREGATION (3 & 4) Ranking 4 Ranking 1 SCHEME 2 AGGREGATION (1 & 3) Ranking 3 FINAL AGGREGATION Ranking 2 AGGREGATION (2 & 4) Ranking 4

Example: Integration tables (Glotov & Paveljev) S = A*B = A*(C*D) B=C*D Scale for

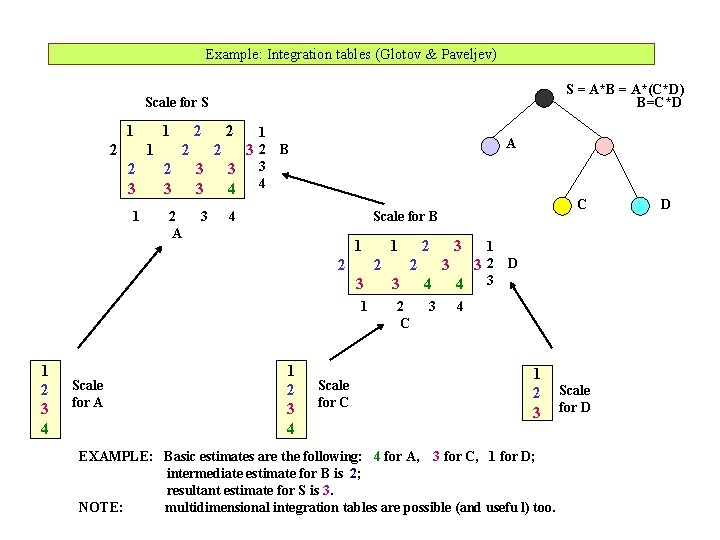
Example: Integration tables (Glotov & Paveljev) S = A*B = A*(C*D) B=C*D Scale for S 1 1 2 2 32 2 2 3 3 3 4 4 1 2 A 3 A B 4 1 Scale for A 1 2 3 1 2 2 2 3 3 4 4 3 1 1 2 3 4 C Scale for B 1 2 3 4 Scale for C 2 C 3 D 4 1 2 3 EXAMPLE: Basic estimates are the following: 4 for A, 3 for C, 1 for D; intermediate estimate for B is 2; resultant estimate for S is 3. NOTE: multidimensional integration tables are possible (and usefu l) too. Scale for D D

Mapping & Optimization Models y=f (x) x R f(x 2) f(x 1) x 1

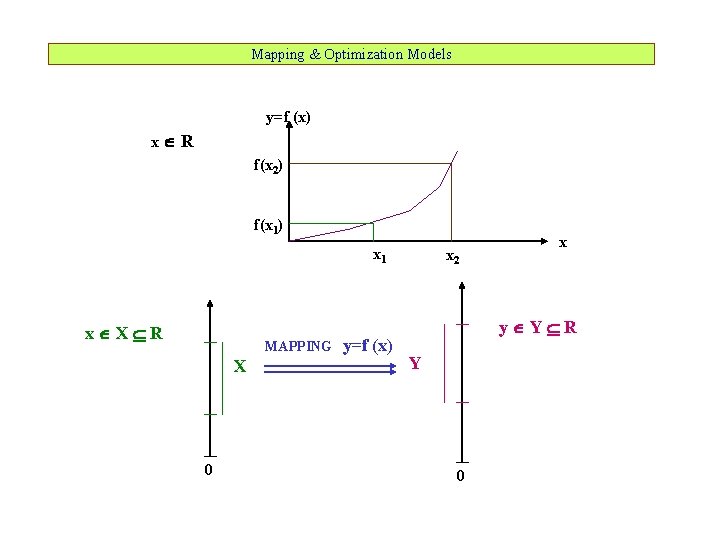
Mapping & Optimization Models y=f (x) x R f(x 2) f(x 1) x 1 x X R MAPPING X 0 y=f (x) x 2 x y Y R Y 0

Mapping & Optimization Models z z = f(x 1, x 2) R 2 (x

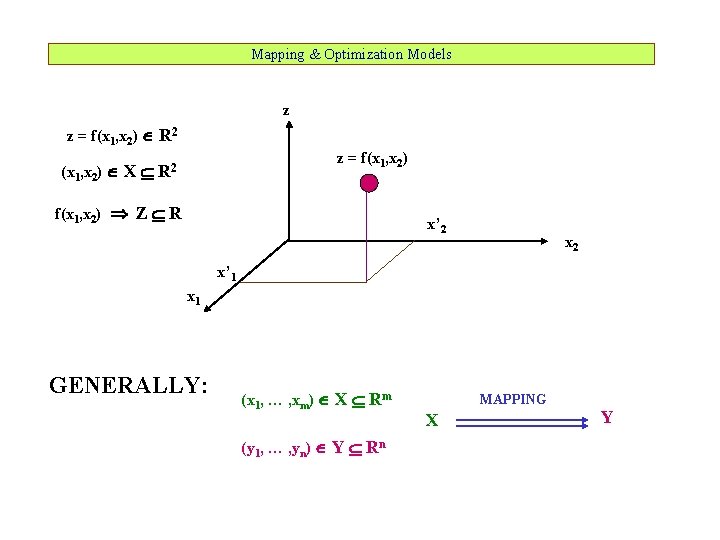
Mapping & Optimization Models z z = f(x 1, x 2) R 2 (x 1, x 2) X z = f(x 1, x 2) R 2 f(x 1, x 2) Z R x’ 2 x’ 1 x 1 GENERALLY: (x 1, … , xm) X Rm (y 1, … , yn) Y Rn MAPPING X Y

Mapping & Optimization Models y=f (x) x X R X =[ x 1, x

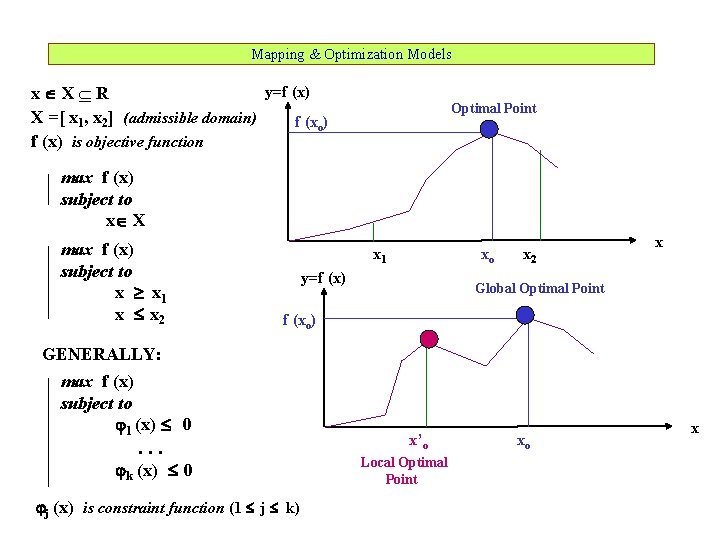
Mapping & Optimization Models y=f (x) x X R X =[ x 1, x 2] (admissible domain) f (xo) f (x) is objective function Optimal Point max f (x) subject to x X max f (x) subject to x x 1 x x 2 x 1 xo y=f (x) x 2 x Global Optimal Point f (xo) GENERALLY: max f (x) subject to 1 (x) 0 . . . k (x) 0 j (x) is constraint function (1 j k) x’o Local Optimal Point xo x

Illustration table for optimization models Objective function f (x) Linear Constraint j (x) Linear

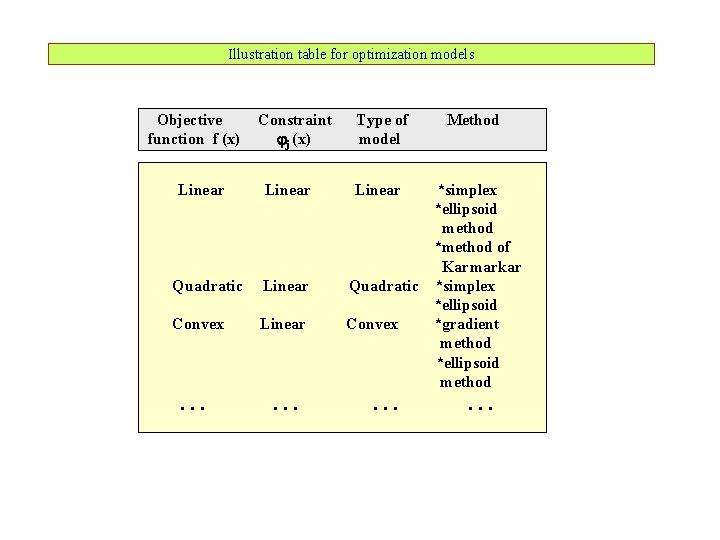
Illustration table for optimization models Objective function f (x) Linear Constraint j (x) Linear Quadratic Linear Convex Linear . . . Type of model Method Linear *simplex *ellipsoid method *method of Karmarkar Quadratic *simplex *ellipsoid Convex *gradient method *ellipsoid method . . .

Integration (aggregation) approaches NOTES: 1. Objective function can be examined as vector-like one too

Integration (aggregation) approaches NOTES: 1. Objective function can be examined as vector-like one too (multi-objective optimization) 2. Constraints can be examined as binary relations too 3. In discrete optimization discrete spaces are examined 4. In stochastic optimization all parameters / functions can be stochastic ones 5. It is possible to take into account uncertainty by two ways: *stochastic parameters / functions *parameters / functions on the basis of fuzzy sets