Lecture 11 1 Ideal vs Real Battery Ideal

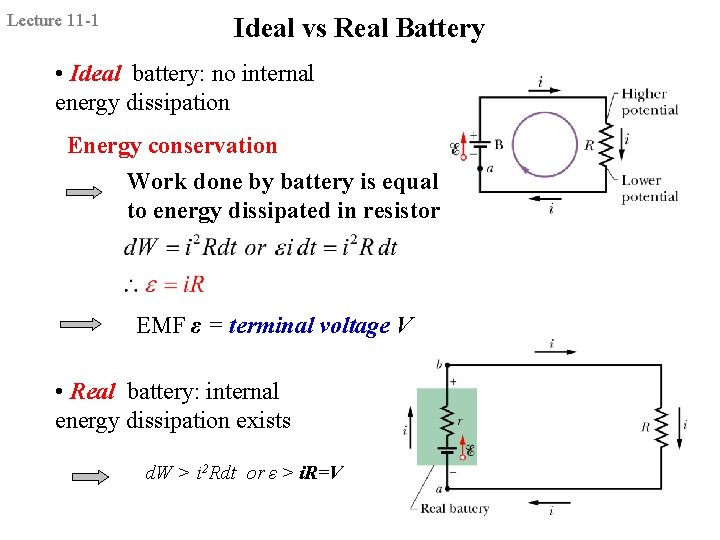
Lecture 11 -1 Ideal vs Real Battery • Ideal battery: no internal energy dissipation Energy conservation Work done by battery is equal to energy dissipated in resistor EMF ε = terminal voltage V • Real battery: internal energy dissipation exists d. W > i 2 Rdt or ε > i. R=V

Lecture 11 -2 Resistors in Series Ø The current through devices in series is always the same. i R 1 R 2 ε For multiple resistors in series: i i Req ε

Lecture 11 -3 Real Battery = Resistors in Series Ø The current through devices in series is always the same. i Req terminal voltage ε internal resistance For multiple resistors in series:

Lecture 11 -4 DOCCAM 2

Lecture 11 -5

Lecture 11 -6 Resistors in Parallel Devices in parallel has the same potential drop Generally, • • •

Lecture 11 -7 Kirchhoff’s Rules Kirchhoff’s Rule 1: Loop Rule v When any closed loop is traversed completely in a circuit, the algebraic sum of the changes in potential is equal to zero. Ø Coulomb force is conservative Kirchhoff’s Rule 2: Junction Rule v The sum of currents entering any junction in a circuit is equal to the sum of currents leaving that junction. Ø Conservation of charge Ø In and Out branches Ø Assign Ii to each branch

Lecture 11 -8 Kirchhoff’s Loop Rule Example v When any closed loop is traversed completely in a circuit, the algebraic sum of the changes in potential is equal to zero. where is the potential difference across i-th device in the circuit: positive if potential rises negative if potential drops terminal voltage

Lecture 11 -9 Loop Example with Two EMF Devices Ir 1 IR 2 ε 1 Ir 2 IR 3 If ε 1 <ε 2, we have I<0 !? This just means the actual current flows reverse to the assumed direction. No problem! Þ

Lecture 11 -10 DOCCAM 2

Lecture 11 -11

Lecture 11 -12 Finding Potential and Power in a Circuit But what is I? Must solve for I first! supplied by 12 V battery The rest? Just means 0 V here into 4 V battery (charging) dissipated by resistors

Lecture 11 -13 Charging a Battery • Positive terminal to positive terminal • Charging EMF > EMF of charged device good battery (12 V) Say, R+r 1+r 2=0. 05Ω (R is for jumper cables). Then, battery being charged (11 V) power into battery 2 • If connected backward, Ø Large amount of gas produced Ø Huge power dissipation in wires

Lecture 11 -14 Using Kirchhoff’s Laws in Multiple Loop Circuits • Identify nodes and use Junction Rule: • Identify independent loops and use Loop Rule: Only two are independent.

Lecture 11 -15 Warm-up quiz 2 I 1+I 2 • What’s the current I 2 ? I 1 (a). 3. 0 A (b). 1. 0 A (c). -2. 0 A (d). -1. 0 A (e). Need more information to calculate the value.

Lecture 11 -16 Another example (with parallel R combos) I 1+I 2 • Sketch the diagram • Simplify using equivalent resistors I 1 • Label currents with directions • Use Junction Rule in labeling • Choose independent loops • Use Loop Rule Replace by equivalent R=2Ω first. • Solve simultaneous linear equations

Lecture 11 -17 Another example (with parallel R combos) I 1+I 2 • Sketch the diagram • Simplify using equivalent resistors I 1 • Label currents with directions • Use Junction Rule in labeling • Choose independent loops • Use Loop Rule Replace by equivalent R=2Ω first. • Solve simultaneous linear equations

Lecture 11 -18 Loop current example (with parallel R combos) I 1 I 2 I 1 -I 2 • Sketch the diagram • Simplify using equivalent resistors • Label loop currents with directions • Use Loop currents I 1 and I 2 • Choose interior clockwise loops. Set up cononical equations in Replace by equivalent R=2Ω first. . I 1 I 2 Ε format I 1 (12 +6) +I 2 (-6) = +18 (Emf) Left loop I 1 (-6) + I 2 (6+3+2) =+21 (Emf) Right loop Note Symmetry of Equations

Lecture 11 -19 Kirchoff Circuit Analysis Tips (Loop current system easier) • Sketch the diagram • Simplify using equivalent resistors • Label currents with directions • Use Junction Rule in labeling • Choose independent loops • Use Loop Rule • Solve simultaneous linear equations

Lecture 11 -20 Ammeter and Voltmeter Ammeter: an instrument used to measure currents • It must be connected in series. • The internal resistance of an ammeter must be kept as small as possible. Voltmeter: an instrument used to measure potential differences • It must be connected in parallel. • The internal resistance of a voltmeter must be made as large as possible.

Lecture 11 -21 Galvanometer Inside Ammeter and Voltmeter Galvanometer: a device that detects small currents and indicates its magnitude. Its own resistance Rg is small for not disturbing what is being measured. galvanometer Ammeter: an instrument used to measure currents shunt resistor Voltmeter: an instrument used to measure potential differences galvanometer

Lecture 11 -22 PHYS 241 – 10: 30 quiz 3 What is the magnitude of the current through R 1 ? a. 0. 575 A b. 0. 5 A c. 0. 75 A d. 0. 33 A e. 1. 5 A 30Ω 45 V R 1 R 3 R 2 30Ω 45 V

Lecture 11 -23 PHYS 241 – 11: 30 quiz 3 What is the magnitude of the current through R 2 ? a. 0. 33 A b. 2. 5 A c. 0. 75 A d. 1. 5 A e. 0. 3. A 10Ω 15 V R 1 R 3 R 2 10Ω 15 V

Lecture 11 -24 PHYS 241 – Quiz 11 C What is the current through R 3 ? a. 0. 375 A b. 0. 5 A c. 0. 75 A d. 1 A e. 1. 5 A 20Ω 30 V R 1 R 3 R 2 20Ω 30 V