Lecture 10 Static ILP Basics Topics loop unrolling

Lecture 10: Static ILP Basics • Topics: loop unrolling, static branch prediction, VLIW (Sections 4. 1 – 4. 4) 1

Static vs Dynamic Scheduling • Arguments against dynamic scheduling: Ø requires complex structures to identify independent instructions (scoreboards, issue queue) § high power consumption § low clock speed § high design and verification effort Ø the compiler can “easily” compute instruction latencies and dependences – complex software is always preferred to complex hardware (? ) 2

Loop Scheduling • Revert back to the 5 -stage in-order pipeline • The compiler’s job is to minimize stalls • Focus on loops: account for most cycles, relatively easy to analyze and optimize • Recall: a load has a two-cycle latency (1 stall cycle for the consumer that immediately follows), FP ALU feeding another 3 stall cycles, FP ALU feeding a store 2 stall cycles 3
![Loop Example for (i=1000; i>0; i--) x[i] = x[i] + s; Loop: Source code Loop Example for (i=1000; i>0; i--) x[i] = x[i] + s; Loop: Source code](http://slidetodoc.com/presentation_image_h2/01d3cfa89d1c84a5b58c61c4679da286/image-4.jpg)
Loop Example for (i=1000; i>0; i--) x[i] = x[i] + s; Loop: Source code L. D F 0, 0(R 1) ADD. D F 4, F 0, F 2 S. D F 4, 0(R 1) DADDUI R 1, # -8 BNE R 1, R 2, Loop ; F 0 = array element ; add scalar ; store result ; decrement address pointer ; branch if R 1 != R 2 L. D F 0, 0(R 1) stall ADD. D F 4, F 0, F 2 stall S. D F 4, 0(R 1) DADDUI R 1, # -8 stall BNE R 1, R 2, Loop stall ; F 0 = array element Assembly code ; add scalar ; store result ; decrement address pointer 10 -cycle schedule ; branch if R 1 != R 2 4
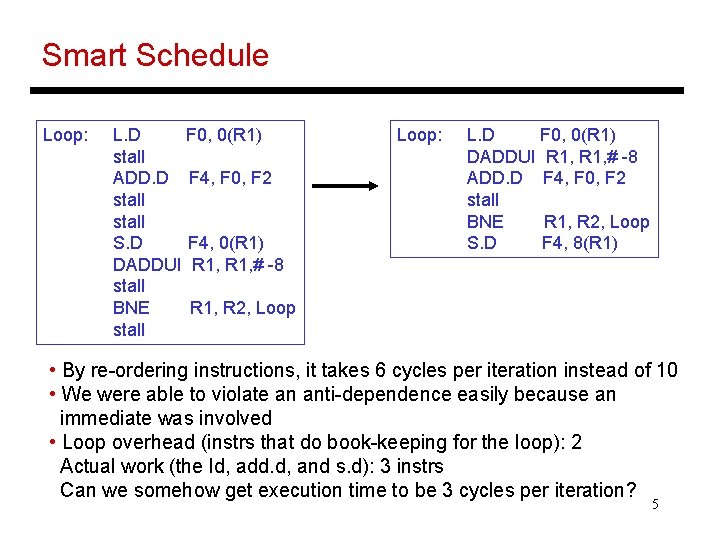
Smart Schedule Loop: L. D F 0, 0(R 1) stall ADD. D F 4, F 0, F 2 stall S. D F 4, 0(R 1) DADDUI R 1, # -8 stall BNE R 1, R 2, Loop stall Loop: L. D F 0, 0(R 1) DADDUI R 1, # -8 ADD. D F 4, F 0, F 2 stall BNE R 1, R 2, Loop S. D F 4, 8(R 1) • By re-ordering instructions, it takes 6 cycles per iteration instead of 10 • We were able to violate an anti-dependence easily because an immediate was involved • Loop overhead (instrs that do book-keeping for the loop): 2 Actual work (the ld, add. d, and s. d): 3 instrs Can we somehow get execution time to be 3 cycles per iteration? 5

Loop Unrolling Loop: L. D F 0, 0(R 1) ADD. D F 4, F 0, F 2 S. D F 4, 0(R 1) L. D F 6, -8(R 1) ADD. D F 8, F 6, F 2 S. D F 8, -8(R 1) L. D F 10, -16(R 1) ADD. D F 12, F 10, F 2 S. D F 12, -16(R 1) L. D F 14, -24(R 1) ADD. D F 16, F 14, F 2 S. D F 16, -24(R 1) DADDUI R 1, #-32 BNE R 1, R 2, Loop • Loop overhead: 2 instrs; Work: 12 instrs • How long will the above schedule take to complete? 6

Scheduled and Unrolled Loop: L. D F 0, 0(R 1) L. D F 6, -8(R 1) L. D F 10, -16(R 1) L. D F 14, -24(R 1) ADD. D F 4, F 0, F 2 ADD. D F 8, F 6, F 2 ADD. D F 12, F 10, F 2 ADD. D F 16, F 14, F 2 S. D F 4, 0(R 1) S. D F 8, -8(R 1) DADDUI R 1, # -32 S. D F 12, 16(R 1) BNE R 1, R 2, Loop S. D F 16, 8(R 1) • Execution time: 14 cycles or 3. 5 cycles per original iteration 7

Loop Unrolling • Increases program size • Requires more registers • To unroll an n-iteration loop by degree k, we will need (n/k) iterations of the larger loop, followed by (n mod k) iterations of the original loop 8

Automating Loop Unrolling • Determine the dependences across iterations: in the example, we knew that loads and stores in different iterations did not conflict and could be re-ordered • Determine if unrolling will help – possible only if iterations are independent • Determine address offsets for different loads/stores • Dependency analysis to schedule code without introducing hazards; eliminate name dependences by using additional registers 9

Superscalar Pipelines Loop: Integer pipeline L. D F 0, 0(R 1) L. D F 6, -8(R 1) L. D F 10, -16(R 1) L. D F 14, -24(R 1) L. D F 18, -32(R 1) S. D F 4, 0(R 1) S. D F 8, -8(R 1) S. D F 12, -16(R 1) DADDUI R 1, # -40 S. D F 16, 16(R 1) BNE R 1, R 2, Loop S. D F 20, 8(R 1) FP pipeline ADD. D F 4, F 0, F 2 F 8, F 6, F 2 F 12, F 10, F 2 F 16, F 14, F 20, F 18, F 2 • The compiler may specify instructions that can be issued as one packet • The compiler may specify a fixed number of instructions in each packet: Very Large Instruction Word (VLIW) 10

Loop Dependences • If a loop only has dependences within an iteration, the loop is considered parallel multiple iterations can be executed together so long as order within an iteration is preserved • If a loop has dependeces across iterations, it is not parallel and these dependeces are referred to as “loop-carried” • Not all loop-carried dependences imply lack of parallelism 11
![Examples For (i=1000; i>0; i=i-1) x[i] = x[i] + s; For (i=1; i<=100; i=i+1) Examples For (i=1000; i>0; i=i-1) x[i] = x[i] + s; For (i=1; i<=100; i=i+1)](http://slidetodoc.com/presentation_image_h2/01d3cfa89d1c84a5b58c61c4679da286/image-12.jpg)
Examples For (i=1000; i>0; i=i-1) x[i] = x[i] + s; For (i=1; i<=100; i=i+1) { A[i+1] = A[i] + C[i]; B[i+1] = B[i] + A[i+1]; } S 1 S 2 For (i=1; i<=100; i=i+1) { A[i] = A[i] + B[i]; B[i+1] = C[i] + D[i]; } S 1 S 2 For (i=1000; i>0; i=i-1) x[i] = x[i-3] + s; S 1 12
![Examples For (i=1000; i>0; i=i-1) x[i] = x[i] + s; No dependences For (i=1; Examples For (i=1000; i>0; i=i-1) x[i] = x[i] + s; No dependences For (i=1;](http://slidetodoc.com/presentation_image_h2/01d3cfa89d1c84a5b58c61c4679da286/image-13.jpg)
Examples For (i=1000; i>0; i=i-1) x[i] = x[i] + s; No dependences For (i=1; i<=100; i=i+1) { A[i+1] = A[i] + C[i]; B[i+1] = B[i] + A[i+1]; } S 1 S 2 depends on S 1 in the same iteration S 1 depends on S 1 from prev iteration S 2 depends on S 2 from prev iteration For (i=1; i<=100; i=i+1) { A[i] = A[i] + B[i]; B[i+1] = C[i] + D[i]; } S 1 S 2 S 1 depends on S 2 from prev iteration For (i=1000; i>0; i=i-1) x[i] = x[i-3] + s; S 1 depends on S 1 from 3 prev iterations Referred to as a recursion Dependence distance 3; limited parallelism 13

Constructing Parallel Loops If loop-carried dependences are not cyclic (S 1 depending on S 1 is cyclic), loops can be restructured to be parallel For (i=1; i<=100; i=i+1) { A[i] = A[i] + B[i]; B[i+1] = C[i] + D[i]; } S 1 S 2 S 1 depends on S 2 from prev iteration A[1] = A[1] + B[1]; For (i=1; i<=99; i=i+1) { B[i+1] = C[i] + D[i]; A[i+1] = A[i+1] + B[i+1]; } B[101] = C[100] + D[100]; S 3 S 4 depends on S 3 of same iteration 14

Static Branch Prediction • To avoid stalls, we may hoist instructions above branches – it helps if these instructions are along the correct path • Static branch prediction enables scheduling decisions by determining the commonly executed path • Simple heuristics: always taken, backward branches are usually taken (loops), forward branches are usually not taken, etc. – most have mispredict ratios of 30 -40% • Profiling helps because branch behavior usually has a bimodal distribution – branches are highly biased as taken or not taken – mispredict ratios 5 -22% 15

Title • Bullet 16
- Slides: 16