LECTURE 10 Simple Linear Regression and Correlation Analyses

LECTURE 10 Simple Linear Regression and Correlation Analyses LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 1

OBJECTIVES Upon completion of this lecture , the student will be able to: The overall objective of this lecture is to give you an understanding of bivariate linear regression analysis, thereby enabling you to: 1. Calculate the Pearson product-moment correlation coefficient to determine if there is a 2. correlation between two variables. 3. Explain what regression analysis is and the concepts of independent and dependent 4. variable. 5. Calculate the slope and y-intercept of the least squares equation of a regression line and 6. from those, determine the equation of the regression line LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 2

CORRELATION AND REGRESSION Two continuous Variables are included. Called (X, Y). The measure that describes the relationship between X and Y is called : Correlation. The measure that predicts a value of one variable, say Y, from the other variable X is called : regression. The analysis starts with a scatter Diagram LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 3

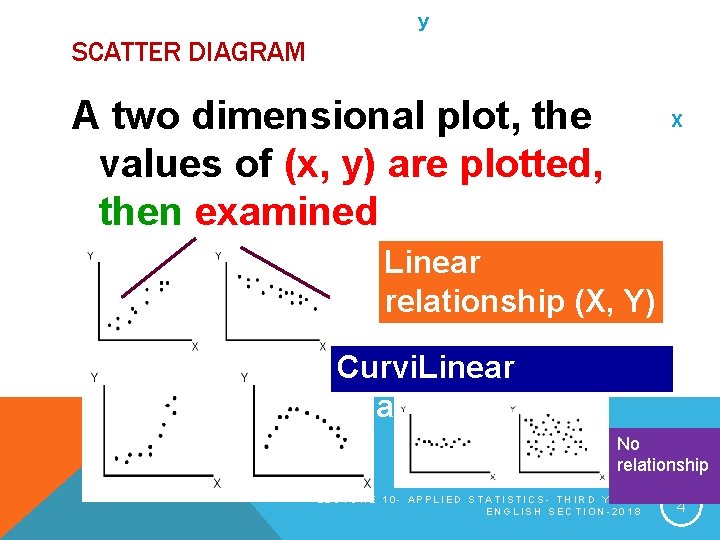
y SCATTER DIAGRAM A two dimensional plot, the values of (x, y) are plotted, then examined X Linear relationship (X, Y) Curvi. Linear relationship (X, Y) No relationship LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 4

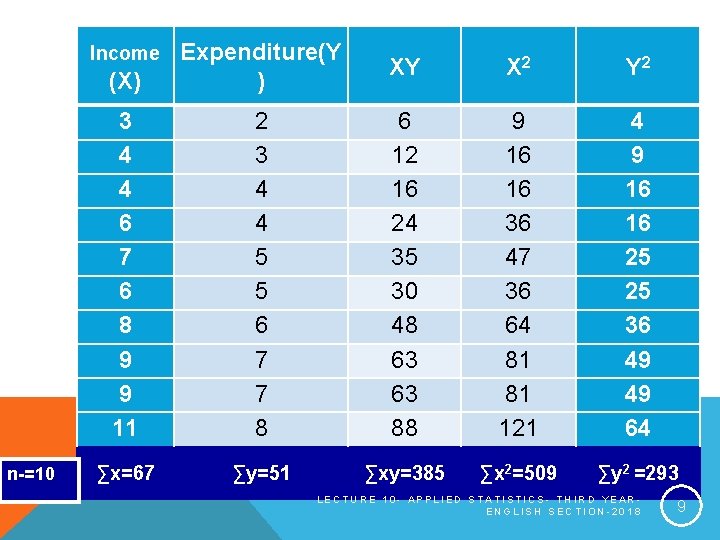
Linear relationship EXAMPLE between income and The following data expenditure gives household income and expenditure in thousands pounds for 10 families: Income Expenditur e 3 4 4 6 7 6 8 9 9 11 2 3 4 4 5 5 6 7 7 8 LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 5

LINEAR CORRELATION : PEARSON’S PRODUCT MOMENT CORRELATION COEFFICIENT LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 6

COMPUTATION OF R LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 7

EXAMPLE, CONT. Income 3 (x) 4 4 6 7 6 8 9 9 11 Expend. 2 e (y) 3 4 4 5 5 6 7 7 8 LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 8

(X) Expenditure(Y ) XY X 2 Y 2 3 4 4 6 7 6 8 9 9 11 2 3 4 4 5 5 6 7 7 8 6 12 16 24 35 30 48 63 63 88 9 16 16 36 47 36 64 81 81 121 4 9 16 16 25 25 36 49 49 64 ∑x=67 ∑y=51 ∑xy=385 ∑x 2=509 ∑y 2 =293 Income n-=10 LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 9

n-=10 Strong direct relationship between expenditure and income LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 10

REGRESSION ANALYSIS When there is association between the two variables, we use one to predict the other The “ Cause” variable is called the independent variable; denoted x The response variable is called the dependent variable; denoted Y. When there is only one independent variable, the regression is simple regression. When there is a linear relationship, regression is called Linear regression LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 11

REGRESSION MODEL The observed values of Y, could be expressed as: Where β 0 : constant β 1 : is the regression coefficient , is the amount of change in the dependent variable associated with one unit increase in the independent variable. LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 12

Xi: value of the independent variable εi: error term due to random differences. The prediction equation is: Thus the random error is: LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 13

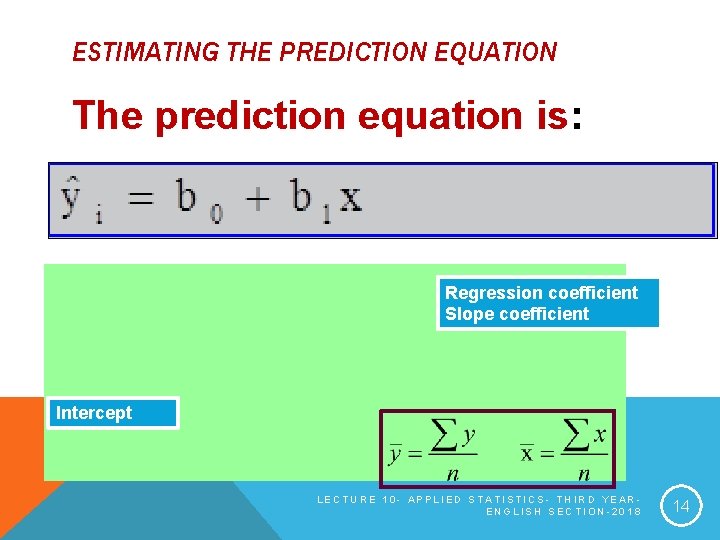
ESTIMATING THE PREDICTION EQUATION The prediction equation is: Regression coefficient Slope coefficient Intercept LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 14

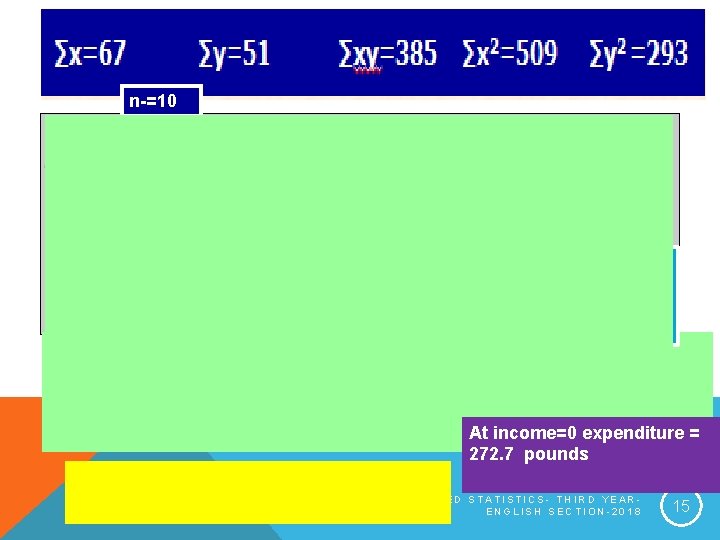
EXAMPLE: n-=10 For every one thousand increase in income expenditure increases by. 7205 ( 000) pounds=720 pounds At income=0 expenditure = 272. 7 pounds LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 15

HOW TO USE THE PREDICTION EQUATION For a family who makes 3 (000) income, the average expenditure is: For a family who makes 4 (000) income, the average expenditure is: LECTURE 10 - APPLIED STATISTICS- THIRD YEAR -ENGLISH SECTION-2018 16

QUESTION(1) 1. Calculate the correlation coefficient for example 1 in chapter 12, where: Ans: r= = -0. 927 LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 17

QUESTION 2 Find the regression equation using the following sums: Ans: b 1=. 162 b 0 =16. 51 LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 18

QUESTION 3 Calculate the error of prediction using the following data and the given prediction equation: LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 19

QUEST FOUR In question (1) the relationship between x and y is: a. Weak b. strong c. Moderate d. Perfect LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 20

QUESTION (5) In question (2) above , as X increases by one unit, y would: a. Increase by 16. 51 b. Decrease by 16. 51 c. Increase by. 162 d. Decrease by. 162 LECTURE 10 - APPLIED STATISTICS- THIRD YEARENGLISH SECTION-2018 21