Lecture 10 Sharding Blockchains full replication Full replication

Lecture 10: Sharding

Blockchains & full replication

Full replication – Consensus problems • Most TP of most consensus decreases with an increase in size of the number of participating nodes • For Nakamoto delay ∝ O(log(N)) • For most BFT based protocols, communication load = O(N^2)

Full replication – resource usage • All nodes process the same transactions • The transaction has to traverse the complete network at least once • All nodes have to store the complete state, the account details of everyone!
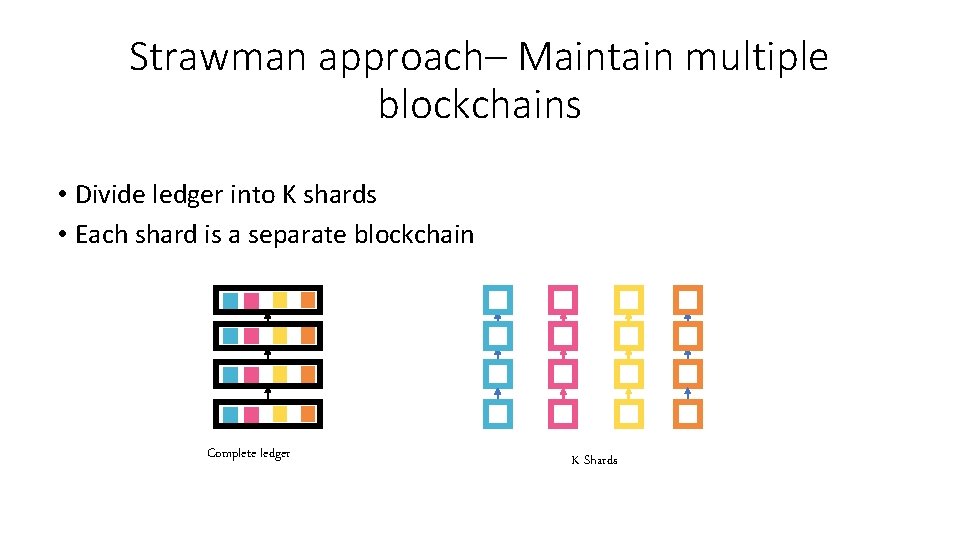
Strawman approach– Maintain multiple blockchains • Divide ledger into K shards • Each shard is a separate blockchain Complete ledger K Shards

Problem • Reduced security – An adversary can concentrate on one shard • How to transfer money from one shard to another? • If such transfer is possible, can transfer non-existent funds from infected shard to non-infected shard.

Coded Sharding: Polyshard X 1 X 2 Xk X 1+X 2 X 5+X 2 X 1+XK X 10+X 21 N nodes • Each node maintains a coded shard • The coded shard is a combination of various uncoded shards X 5 -X 2
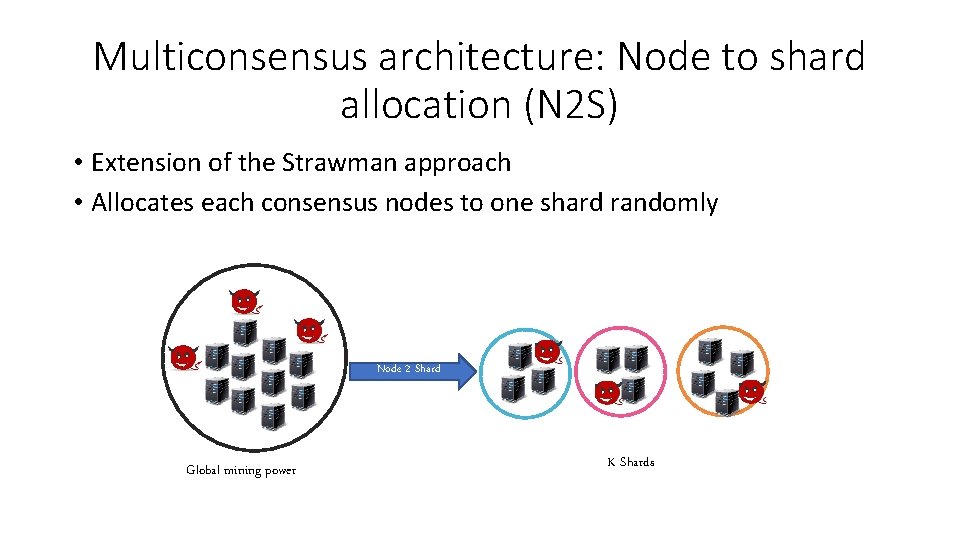
Multiconsensus architecture: Node to shard allocation (N 2 S) • Extension of the Strawman approach • Allocates each consensus nodes to one shard randomly Node 2 Shard Global mining power K Shards
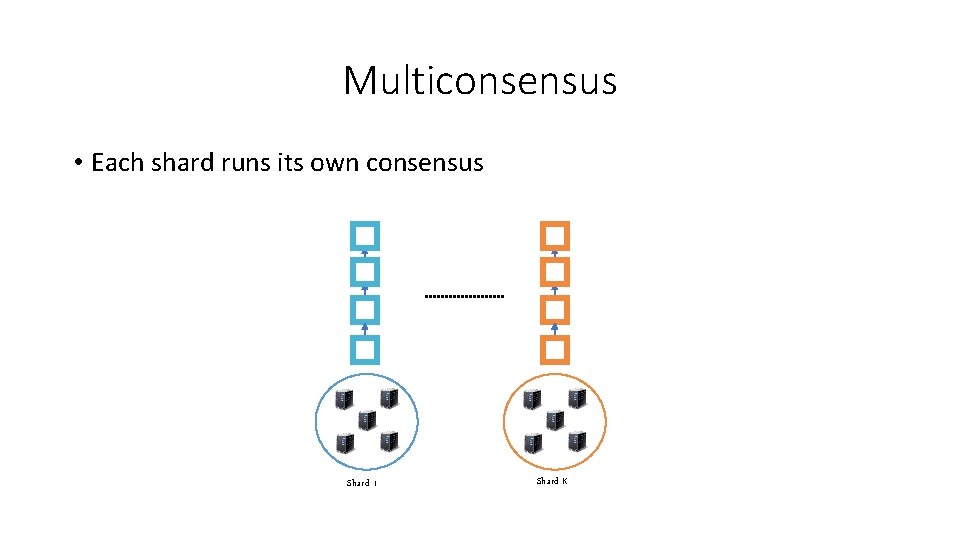
Multiconsensus • Each shard runs its own consensus Shard 1 Shard K
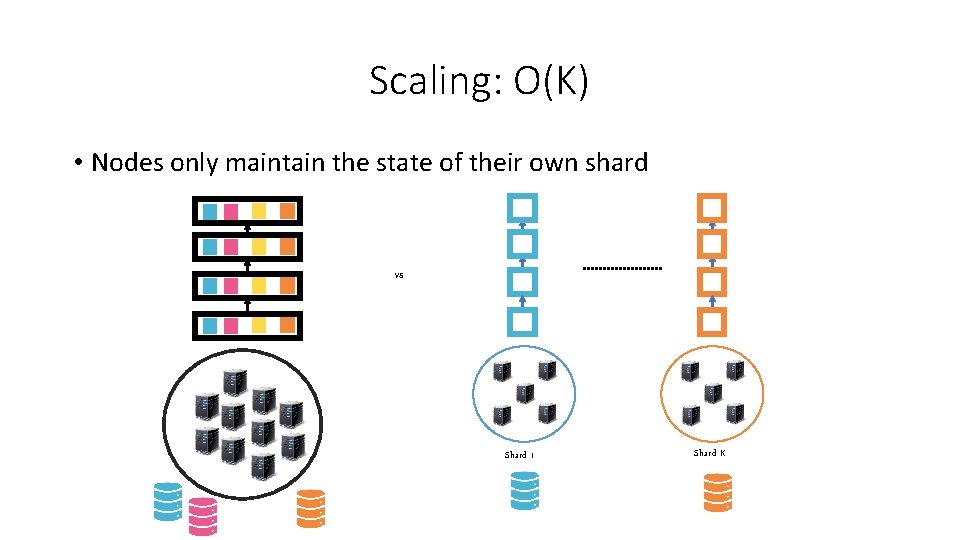
Scaling: O(K) • Nodes only maintain the state of their own shard vs Shard 1 Shard K
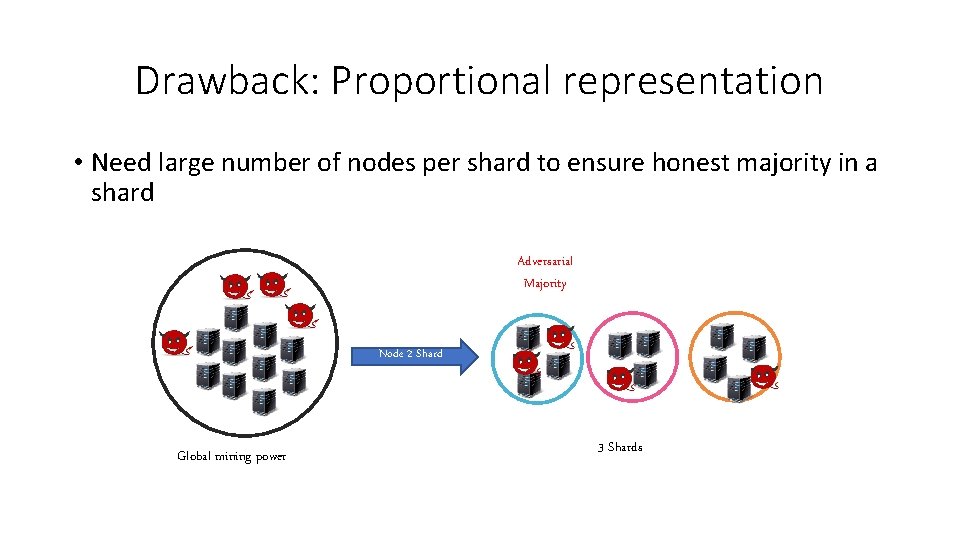
Drawback: Proportional representation • Need large number of nodes per shard to ensure honest majority in a shard Adversarial Majority Node 2 Shard Global mining power 3 Shards
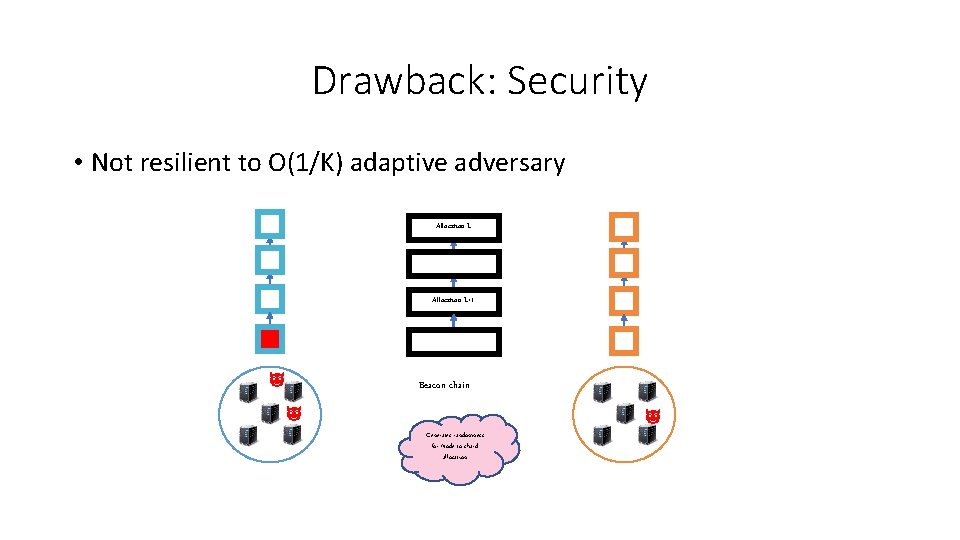
Drawback: Security • Not resilient to O(1/K) adaptive adversary Allocation L+1 Beacon chain Generates randomness for Node to shard allocation

Drawback: Node identity • Existing works vary in the implementation of Node to shard allocation • Different ways of randomness generation • Different rate of re-allocation • All Node to shard allocation algorithms require consensus node identity
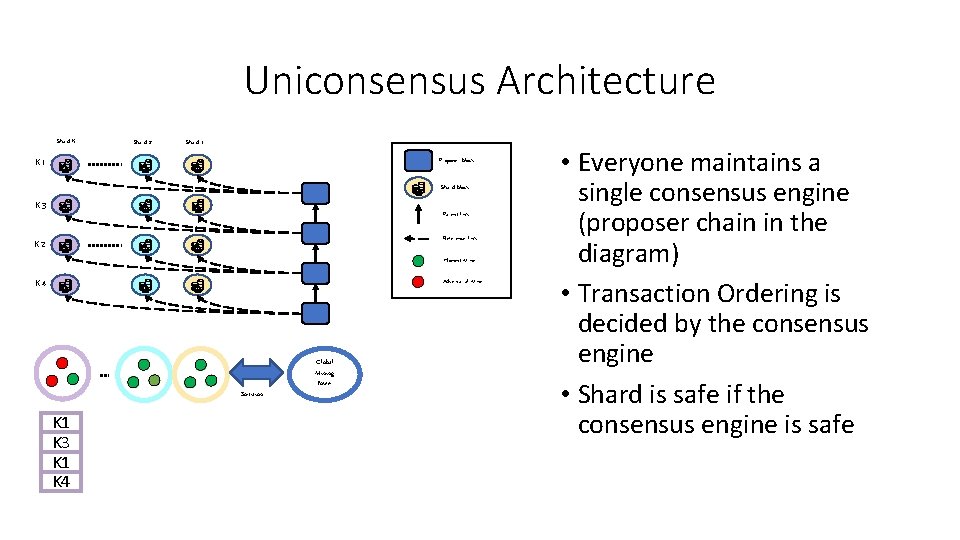
Uniconsensus Architecture Shard K Shard 2 Shard 1 K 1 Proposer block Shard block K 3 Parent link Reference link K 2 Honest Miner Adversarial Miner K 4 Sortition K 1 K 3 K 1 K 4 Global Mining Power • Everyone maintains a single consensus engine (proposer chain in the diagram) • Transaction Ordering is decided by the consensus engine • Shard is safe if the consensus engine is safe
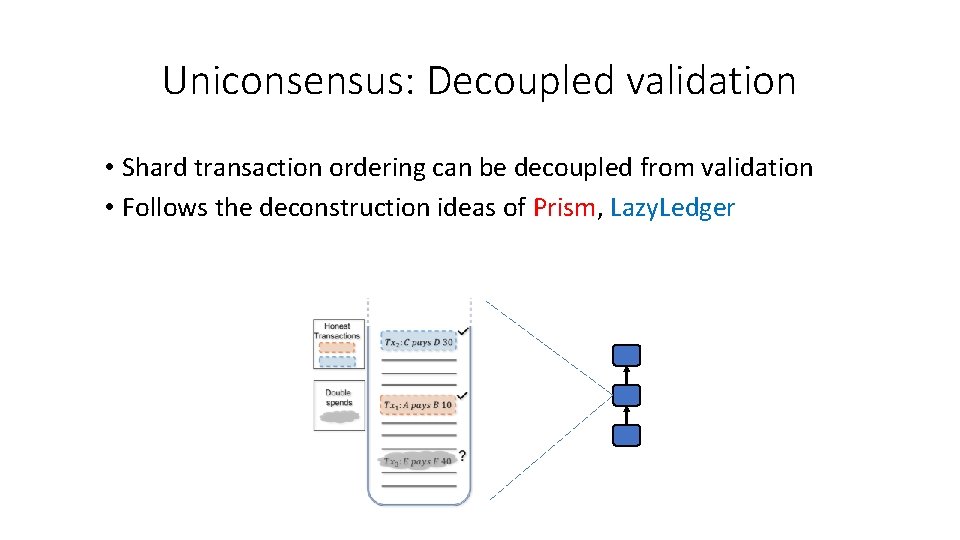
Uniconsensus: Decoupled validation • Shard transaction ordering can be decoupled from validation • Follows the deconstruction ideas of Prism, Lazy. Ledger
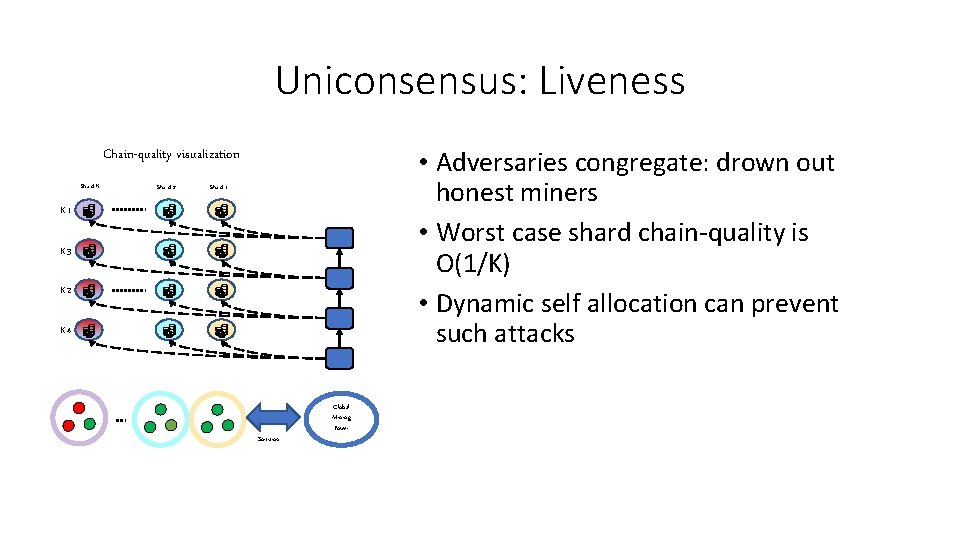
Uniconsensus: Liveness • Adversaries congregate: drown out honest miners • Worst case shard chain-quality is O(1/K) • Dynamic self allocation can prevent such attacks Chain-quality visualization Shard K Shard 2 Shard 1 K 3 K 2 K 4 Sortition Global Mining Power
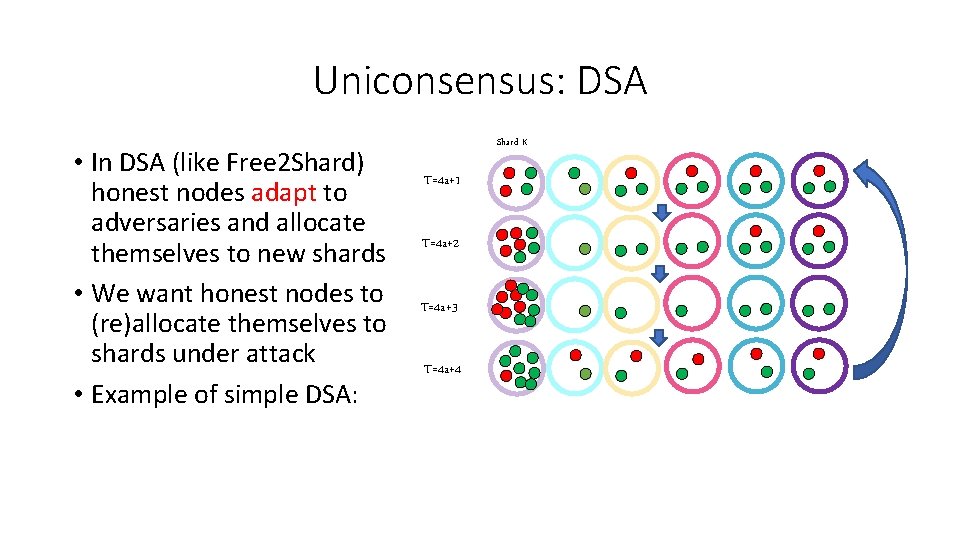
Uniconsensus: DSA • In DSA (like Free 2 Shard) honest nodes adapt to adversaries and allocate themselves to new shards • We want honest nodes to (re)allocate themselves to shards under attack • Example of simple DSA: Shard K T=4 a+1 T=4 a+2 T=4 a+3 T=4 a+4

State commitments: Bootstrapping • Both Uniconsensus and Multiconsensus depend on nodes relocating to new shards • Efficient methods of bootstrapping should be used • Download latest state of a shard (instead of the whole ledger) • Verify state from the latest state-commitment • State-commitment is a root of the Merkle tree of execution state

State-commitments: Multiconsensus • Assumption: Each shard has honest majority • A state-commitment is correct is signed by majority in a shard • OR: A state-commitment is correct if a transaction including one is finalized in the shard’s ledger
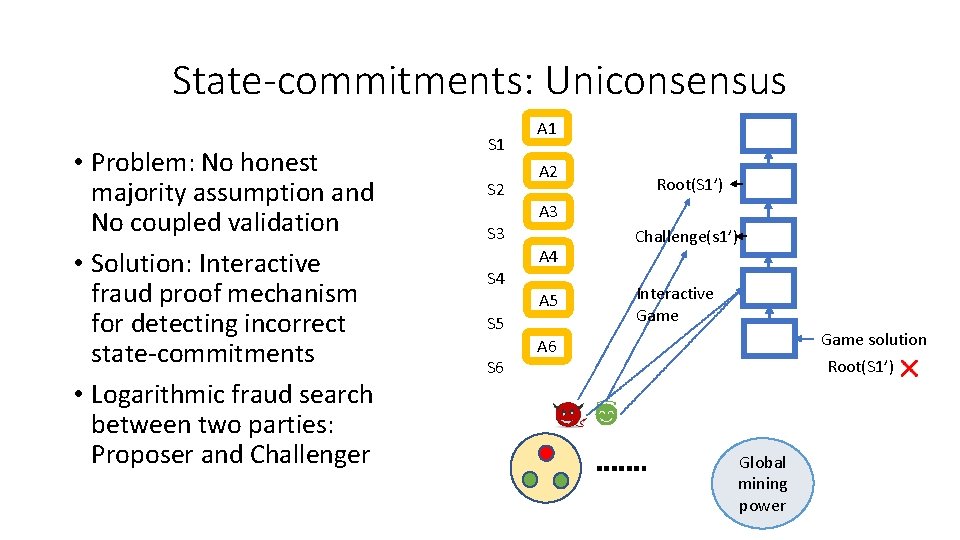
State-commitments: Uniconsensus • Problem: No honest majority assumption and No coupled validation • Solution: Interactive fraud proof mechanism for detecting incorrect state-commitments • Logarithmic fraud search between two parties: Proposer and Challenger S 1 S 2 S 3 A 1 A 2 A 3 A 4 S 4 A 5 S 6 Root(S 1’) Challenge(s 1’) Interactive Game solution A 6 Root(S 1’) Global mining power
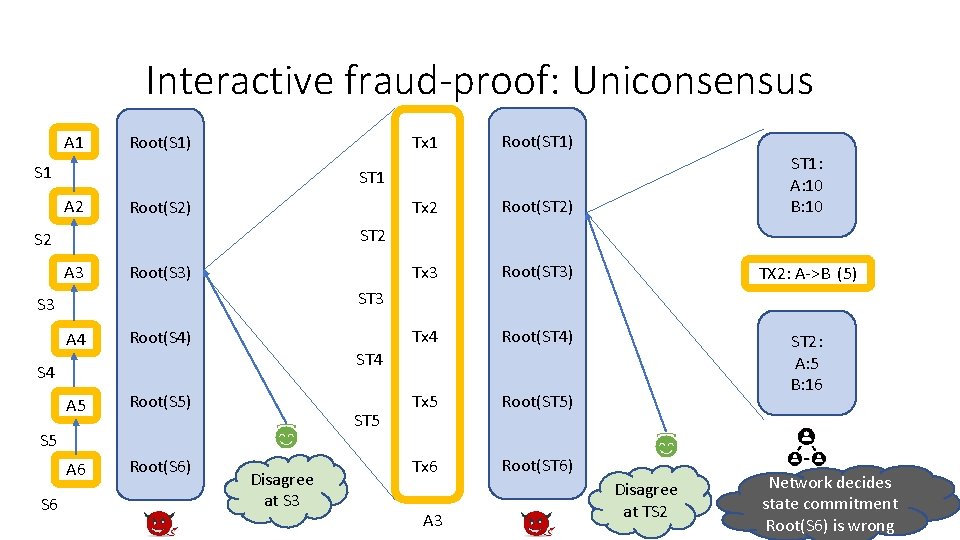
Interactive fraud-proof: Uniconsensus A 1 Root(S 1) S 1 Root(ST 1) Tx 2 Root(ST 2) ST 1: A: 10 B: 10 Tx 3 Root(ST 3) TX 2: A->B (5) Tx 4 Root(ST 4) Tx 5 Root(ST 5) ST 2: A: 5 B: 16 Tx 6 Root(ST 6) ST 1 A 2 Root(S 2) ST 2 S 2 A 3 Root(S 3) ST 3 S 3 A 4 Root(S 4) A 5 Root(S 5) A 6 Root(S 6) ST 4 ST 5 S 6 Tx 1 Disagree at S 3 A 3 Disagree at TS 2 Network decides state commitment Root(S 6) is wrong
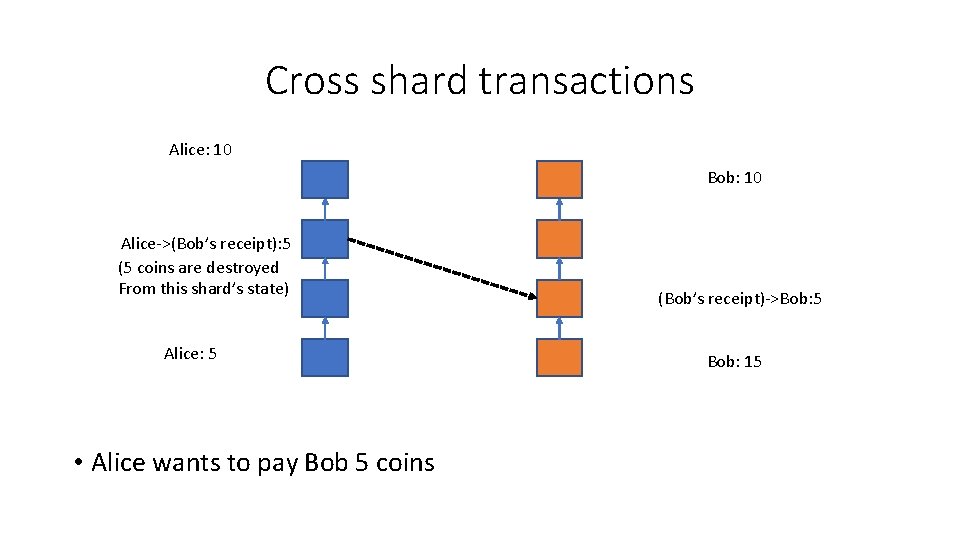
Cross shard transactions Alice: 10 Bob: 10 Alice->(Bob’s receipt): 5 (5 coins are destroyed From this shard’s state) Alice: 5 • Alice wants to pay Bob 5 coins (Bob’s receipt)->Bob: 5 Bob: 15
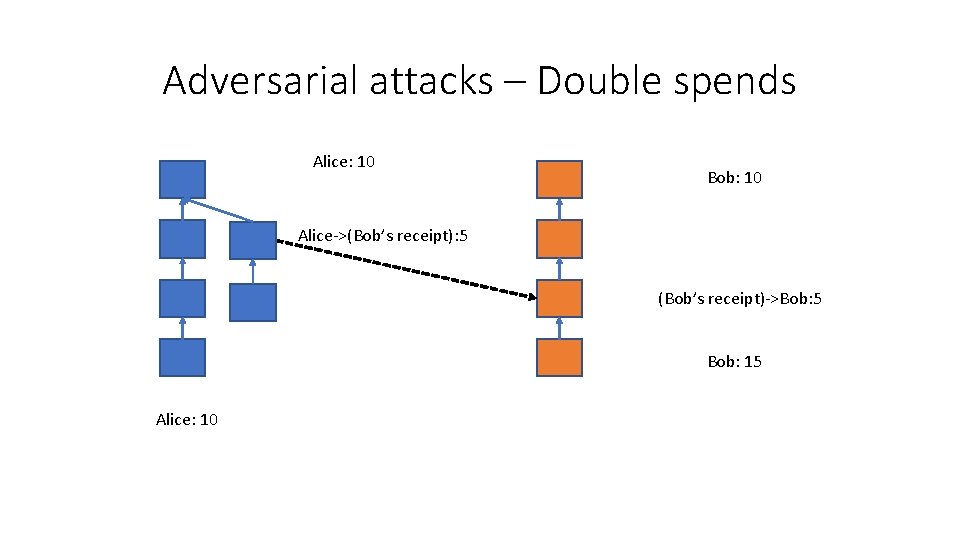
Adversarial attacks – Double spends Alice: 10 Bob: 10 Alice->(Bob’s receipt): 5 (Bob’s receipt)->Bob: 5 Bob: 15 Alice: 10
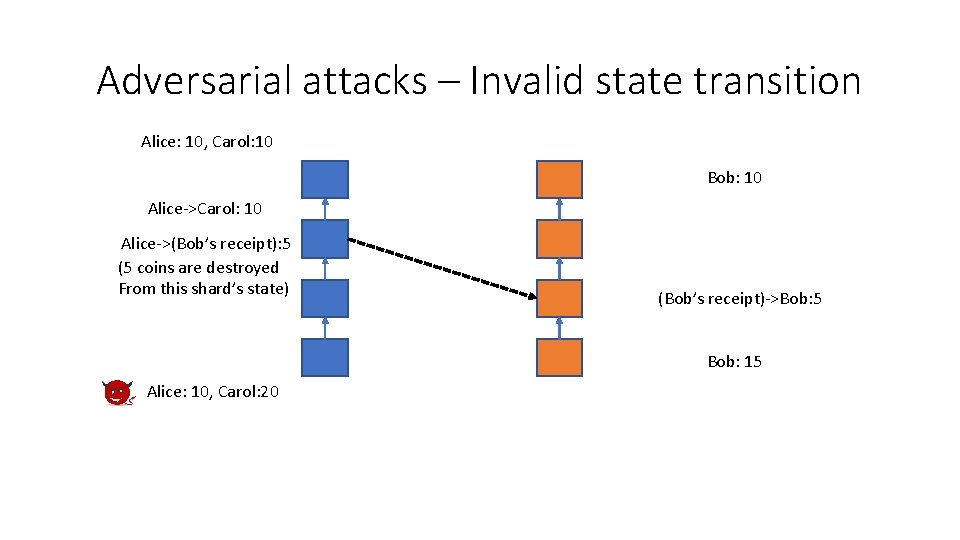
Adversarial attacks – Invalid state transition Alice: 10, Carol: 10 Bob: 10 Alice->Carol: 10 Alice->(Bob’s receipt): 5 (5 coins are destroyed From this shard’s state) (Bob’s receipt)->Bob: 5 Bob: 15 Alice: 10, Carol: 20

Cross-shard transactions • Rely on state-commitments for a foreign-shard’s state • Or rely on a majority signature from foreign-shard’s committee • Atomicity: What if a transactions has multiple input-shards and multiple output-shards • Atomicity: A transactions has to be cancelled on either all of the shards or none of the shards • 2 -Phase commits (2 PC) are used to preserve atomicity
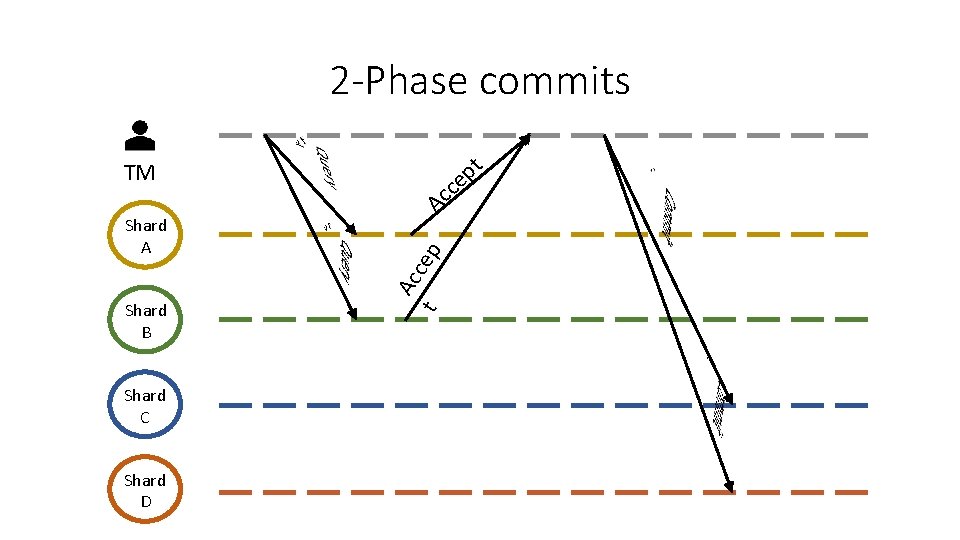
2 -Phase commits t p ce TM Shard B Shard C Shard D p t Ac ce Shard A Ac
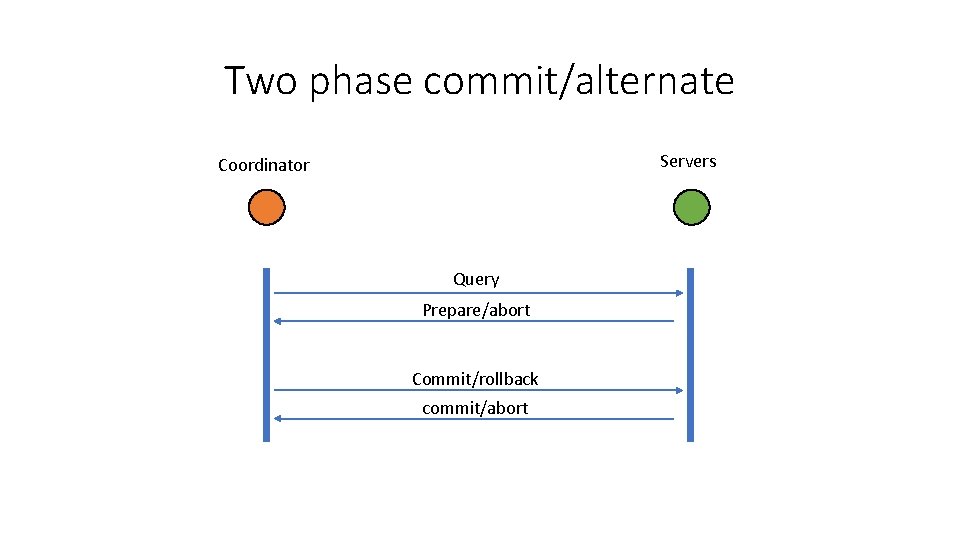
Two phase commit/alternate Servers Coordinator Query Prepare/abort Commit/rollback commit/abort

Thank you
- Slides: 28