Lecture 10 Fourier Transforms Remember homework 1 for

Lecture 10 Fourier Transforms Remember homework 1 for submission 31/10/08 Today • More Fourier fun with examples Remember Phils Problems and your notes = everything http: //www. hep. shef. ac. uk/Phil/PHY 226. htm

Homework 1 hints For part (c) look in your notes or remember from lecture For part (d) The answer should be the first line of the integral that you would perform to find bn. For example ….

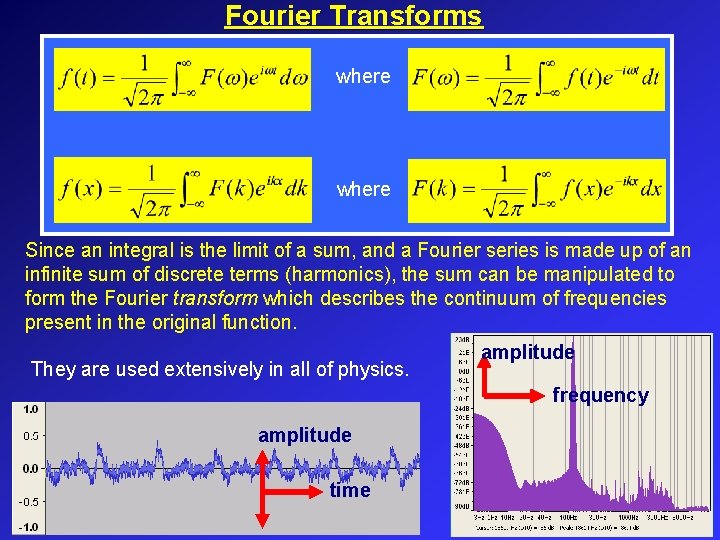
Fourier Transforms where Since an integral is the limit of a sum, and a Fourier series is made up of an infinite sum of discrete terms (harmonics), the sum can be manipulated to form the Fourier transform which describes the continuum of frequencies present in the original function. amplitude They are used extensively in all of physics. frequency amplitude time

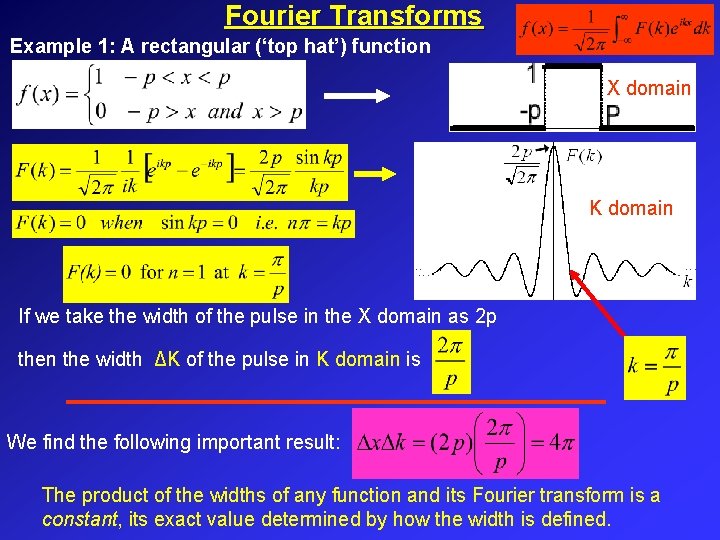
Fourier Transforms Example 1: A rectangular (‘top hat’) function X domain K domain If we take the width of the pulse in the X domain as 2 p then the width ΔK of the pulse in K domain is We find the following important result: The product of the widths of any function and its Fourier transform is a constant, its exact value determined by how the width is defined.

Heisenberg’s Uncertainty Principle The broader the function in real space (x space), the narrower the transform in k space. Or similarly, working with time and frequency, . Therefore … Remember that momentum is related to wave number by Thus and so In quantum physics, the Heisenberg uncertainty principle states that the position and momentum of a particle cannot both be known simultaneously. The more precisely known the value of one, the less precise is the other.

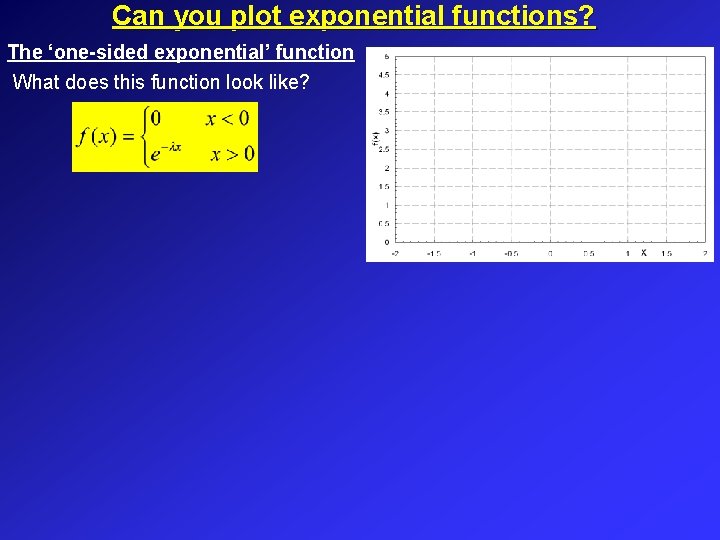
Can you plot exponential functions? The ‘one-sided exponential’ function What does this function look like?

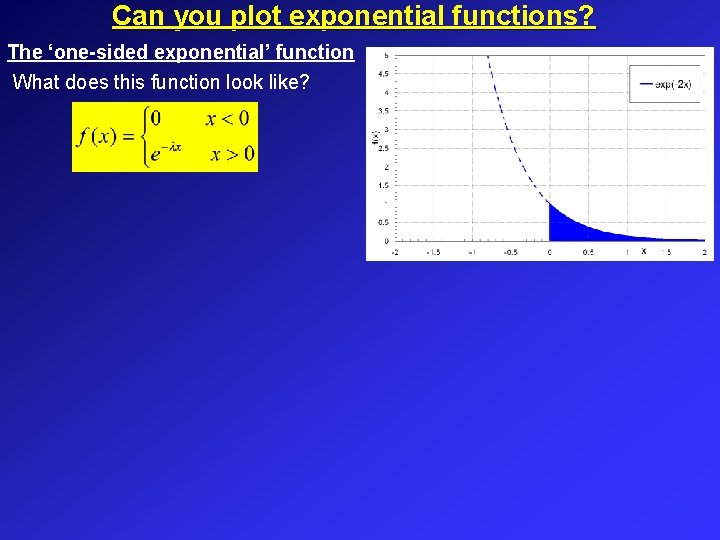
Can you plot exponential functions? The ‘one-sided exponential’ function What does this function look like?

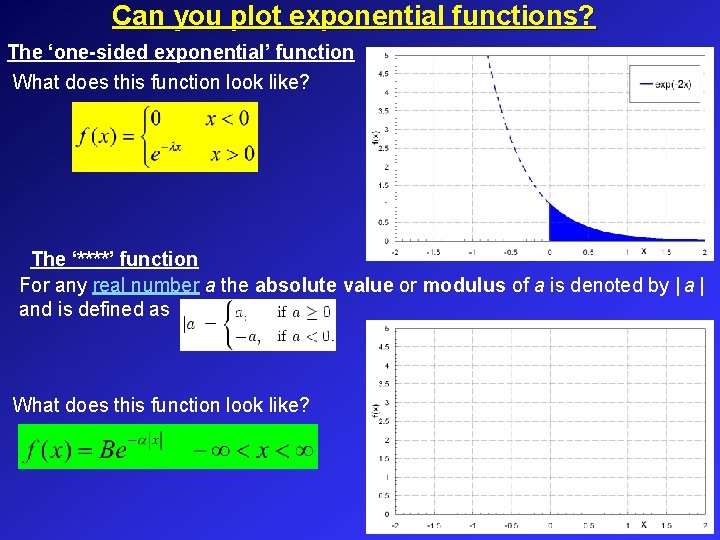
Can you plot exponential functions? The ‘one-sided exponential’ function What does this function look like? The ‘****’ function For any real number a the absolute value or modulus of a is denoted by | and is defined as What does this function look like?

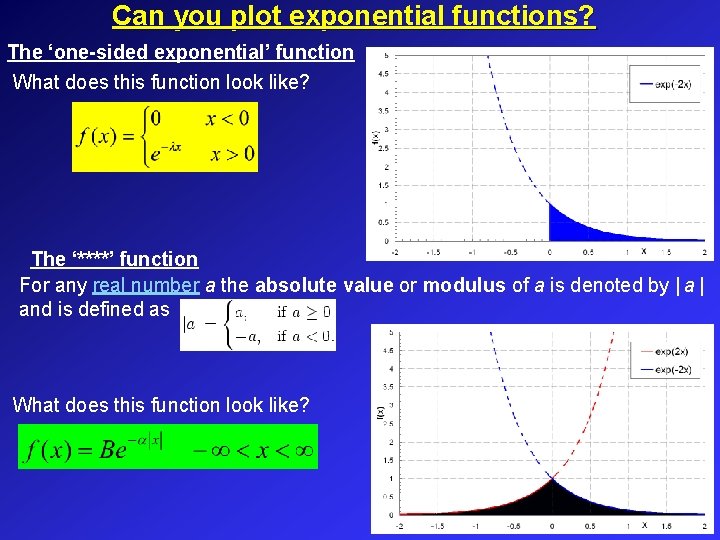
Can you plot exponential functions? The ‘one-sided exponential’ function What does this function look like? The ‘****’ function For any real number a the absolute value or modulus of a is denoted by | and is defined as What does this function look like?

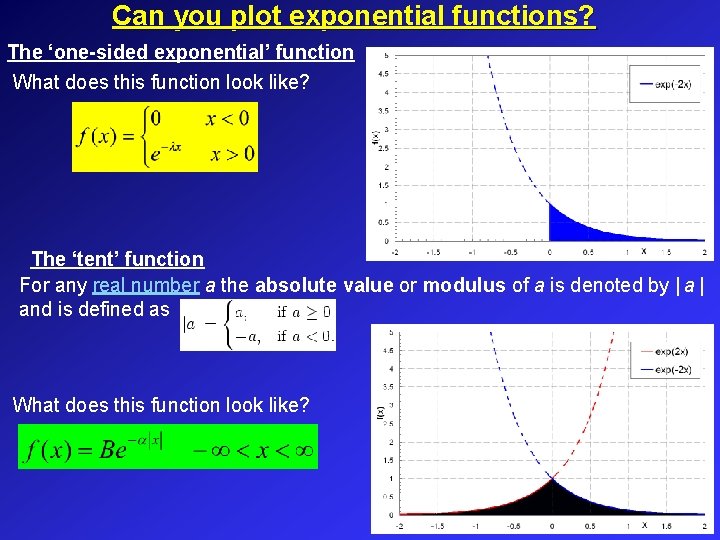
Can you plot exponential functions? The ‘one-sided exponential’ function What does this function look like? The ‘tent’ function For any real number a the absolute value or modulus of a is denoted by | and is defined as What does this function look like?

Fourier Transforms Example 4: The ‘one-sided exponential’ function Show that the function has Fourier transform

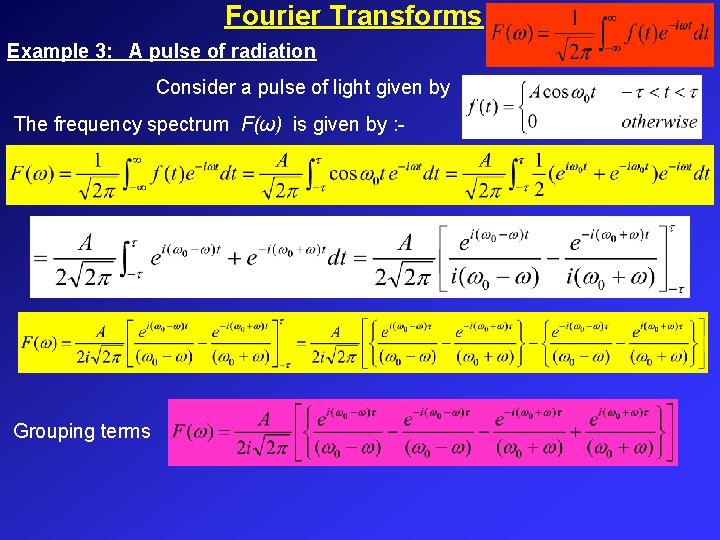
Fourier Transforms Example 3: A pulse of radiation Consider a pulse of light given by The frequency spectrum F(ω) is given by : - Grouping terms

Fourier Transforms Example 3: A pulse of radiation But remember that so we write … Now let’s multiply both top and bottom by t. Often the first term: so the second term is very small and we need only consider

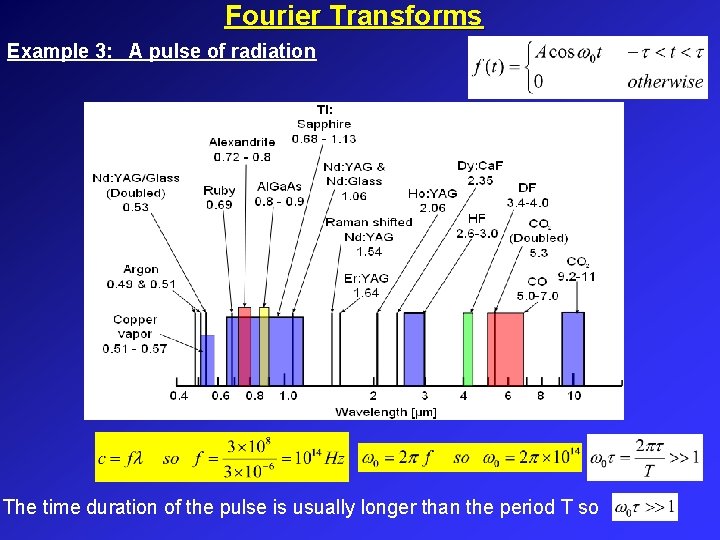
Fourier Transforms Example 3: A pulse of radiation The time duration of the pulse is usually longer than the period T so

Fourier Transforms Example 3: A pulse of radiation But remember that so we write … Now let’s multiply both top and bottom by t. Often so the second term is very small and we need only consider the first term: The frequencies present are essentially those in the range i. e. where so full width of frequencies is If pulse is long, the frequency spread is very small and only frequency observed will be w 0. This is as expected. But for a short pulse there is significant broadening and we can no longer say it is made up of a single frequency.

Fourier Transforms Example 3: A pulse of radiation This result is relevant to pulsed lasers. Ti-sapphire lasers have been developed which give very short pulses of light – pulses lasting just a few femtoseconds to probe relaxation phenomena in solids. However the frequency of the light itself is only a little greater than 1015 Hz so this means that we really have a short cosine wave pulse in time, and the frequency is therefore spread. While CW (continuous wave) lasers can emit light with an extremely narrow line-width, pulsed laser light must, by its very nature, have a broader linewidth. And the shorter the pulse, the broader the line-width. short pulse long pulse

Complexity, Symmetry and the Cosine Transform We know that the Fourier transform from x space into k space can be written as: We also know that we can write So we can say: What is the symmetry of an odd function x an even function ? Odd If f(x) is real and even what can we say about the second integral above ? Will F(k) be real or complex ? 2 nd integral is odd (disappears) and F(k) is real If f(x) is real and odd what can we say about the first integral above ? Will F(k) be real or complex ? 1 st integral is odd (disappears), F(k) is complex What will happen when f(x) is neither odd nor even ? Neither 1 st nor 2 nd integral disappears, and F(k) is usually complex

Complexity, Symmetry and the Cosine Transform Since we say let’s see if we can shorten the amount of maths required for a specific case … f(x) is real and even As before the 2 nd integral is odd, disappears, and F(k) is real so But remember that So LET’S GO BACKWARDS Now since F(k) is real and even it must be true that were we to then find the Fourier transform of F(K) , this can be written: -

Complexity, Symmetry and the Cosine Transform Fourier cosine transform Here is the pair of Fourier transforms which may be used when f(x) is real and even only Example 5: Repeat Example 1 using Fourier cosine transformula above. Find F(k) for this function