Lecture 10 Causal Estimation of 3 D Structure










- Slides: 15

Lecture 10 Causal Estimation of 3 D Structure and Motion MASKS © 2004 Invitation to 3 D vision

VISION as a SENSOR machine to INTERACT with the environment NEED to estimate relative 3 D MOTION 3 D SHAPE (TASK) REAL-TIME CAUSAL processing representation of SHAPE (only supportive of representation of motion) POINT-FEATURES MASKS © 2004 Invitation to 3 D vision

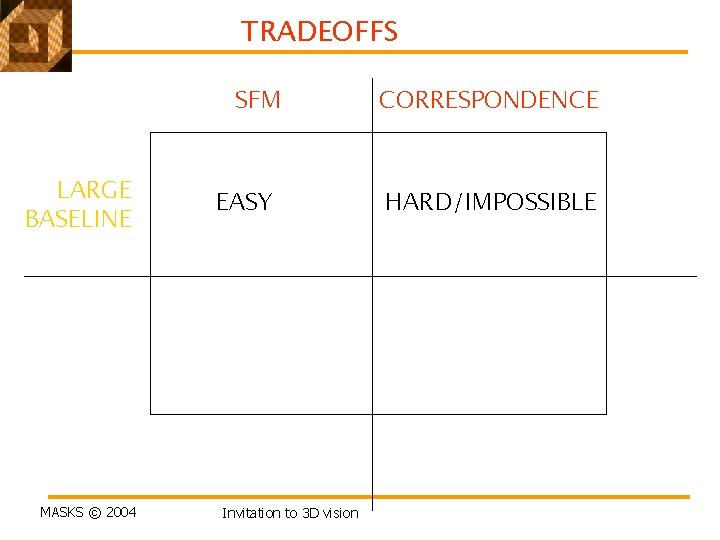
TRADEOFFS SFM LARGE BASELINE MASKS © 2004 EASY Invitation to 3 D vision CORRESPONDENCE HARD/IMPOSSIBLE

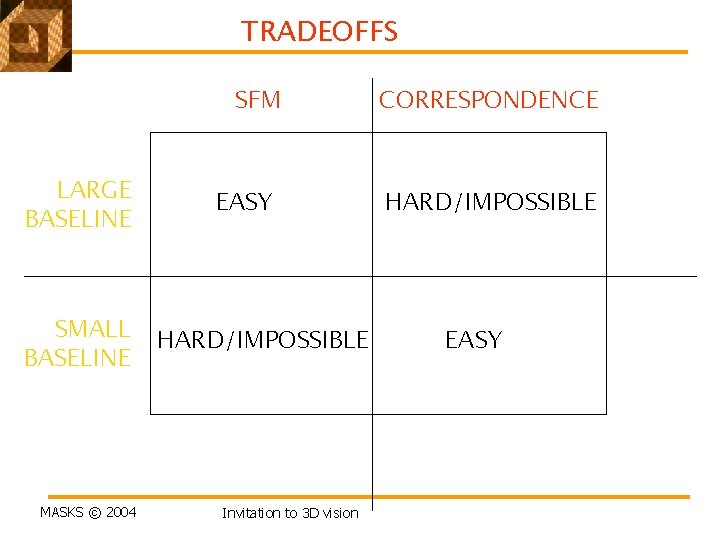
TRADEOFFS SFM LARGE BASELINE SMALL BASELINE MASKS © 2004 EASY HARD/IMPOSSIBLE Invitation to 3 D vision CORRESPONDENCE HARD/IMPOSSIBLE EASY

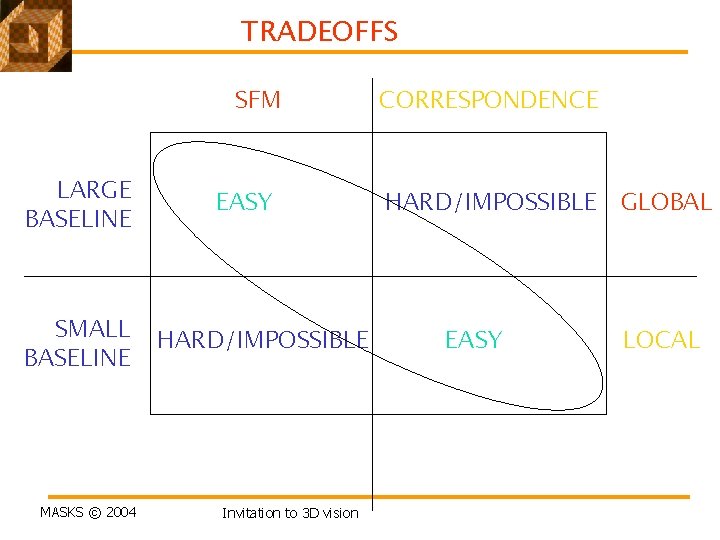
TRADEOFFS SFM LARGE BASELINE SMALL BASELINE MASKS © 2004 EASY HARD/IMPOSSIBLE Invitation to 3 D vision CORRESPONDENCE HARD/IMPOSSIBLE EASY GLOBAL LOCAL

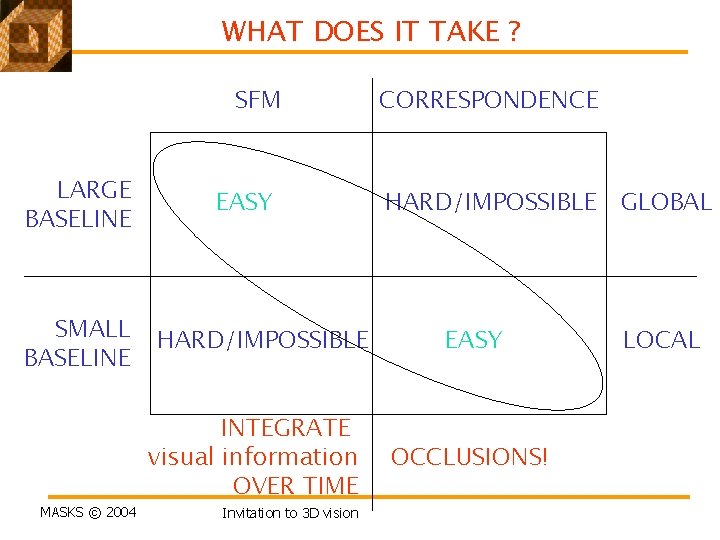
WHAT DOES IT TAKE ? SFM LARGE BASELINE SMALL BASELINE MASKS © 2004 EASY HARD/IMPOSSIBLE INTEGRATE visual information OVER TIME Invitation to 3 D vision CORRESPONDENCE HARD/IMPOSSIBLE EASY OCCLUSIONS! GLOBAL LOCAL

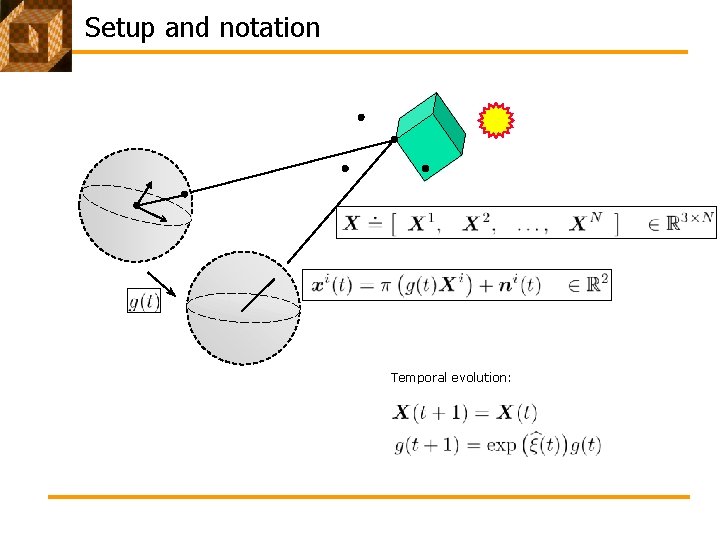
Setup and notation Temporal evolution:

Structure and motion as a filtering problem • • • Given measurements of the “output” (feature point positions) Given modeling assumptions about the “input” (acceleration = noise) Estimate the “state” (3 D structure, pose, velocity) MASKS © 2004 Invitation to 3 D vision

Difficulties … • • Model is non-linear (output map = projection) State-space is non-linear! (SE(3)) Noise: need to specify what we mean by “estimate” Even without noise: model is not observable! MASKS © 2004 Invitation to 3 D vision

Observability • Equivalent class of state-space trajectories generate the same measurements • Fix, e. g. , the direction of 3 points, and the depth of one point (Gauge transformation) MASKS © 2004 Invitation to 3 D vision

Local coordinatization of the state space MASKS © 2004 Invitation to 3 D vision

Minimal realization • Now it looks very much like: • And we are looking for (a point statistic of): MASKS © 2004 Invitation to 3 D vision

EFK vs. particle filter? • • For single rigid body/static scene, expect unimodal posterior No need to estimate entire density; point estimate suffices Robust (M-) version of EKF works well in practice … … and in real time for a few hundred feature points MASKS © 2004 Invitation to 3 D vision

In practice … • • • Adding/removing features (subfilters) Multiple motions/outliers (M-filter, innovation tests) Tracking drift (reset with wide-baseline matching) Switching the reference features (hard! Causes unavoidable global drift) Global registration (maintain DB of lost features) MASKS © 2004 Invitation to 3 D vision

MASKS © 2004 Invitation to 3 D vision