Lecture 1 Semiclassical wavepacket dynamics and the Boltzmann

Lecture 1: Semiclassical wavepacket dynamics and the Boltzmann equation Dimi Culcer UNSW

Outline of this lecture • Wave-packet dynamics • Definition of a wave-packet, Lagrangian and equations of motion • Berry curvature and Berry phase • Combining wave-packet dynamics with the Boltzmann equation • • Intrinsic and extrinsic terms in transport Example: the longitudinal conductivity and the anomalous Hall effect Where does dissipation come from? When can transport be dissipationless? • TODAY WILL BE MORE FORMAL Phys. Rev. B 59, 14915 (1999)

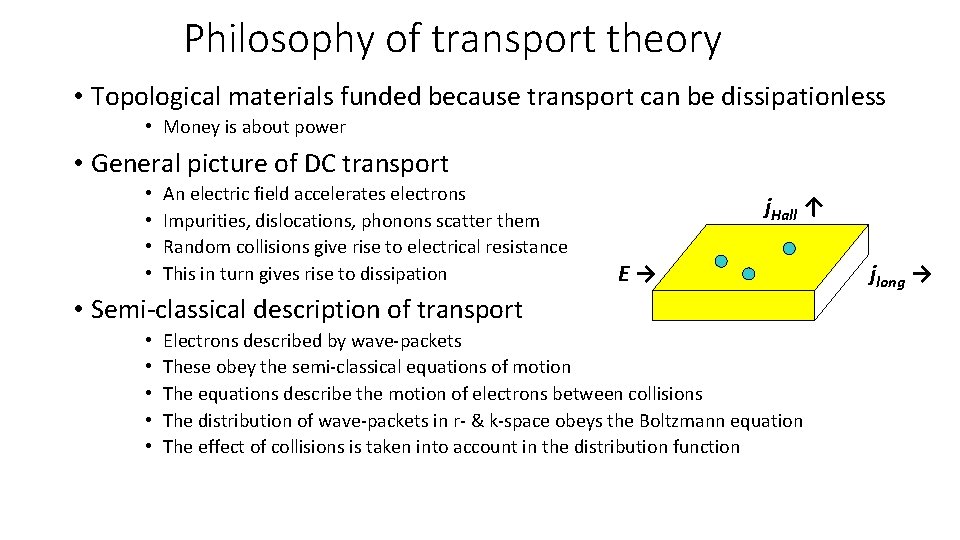
Philosophy of transport theory • Topological materials funded because transport can be dissipationless • Money is about power • General picture of DC transport • • An electric field accelerates electrons Impurities, dislocations, phonons scatter them Random collisions give rise to electrical resistance This in turn gives rise to dissipation j. Hall ↑ E→ • Semi-classical description of transport • • • Electrons described by wave-packets These obey the semi-classical equations of motion The equations describe the motion of electrons between collisions The distribution of wave-packets in r- & k-space obeys the Boltzmann equation The effect of collisions is taken into account in the distribution function jlong →

Justification of the semi-classical model • Why do we need to use wave-packets? • Charge carriers are particles which have a finite size • We need a finite extent in real space • This requires a finite extent in momentum space • In transport we need position and momentum • Especially over large scales over which transport is always diffusive • Spatial gradients important even when applied fields are homogeneous • Electric and magnetic fields are frequently inhomogeneous • They depend on position • Some problems are most easily solved semi-classically • For example Landau-Zener tunnelling • This is solved by WKB (rc, kc)

Assumptions of the semiclassical model • (rc, kc)

Definition of the wave-packet •

Expectation values •

Lagrangian •

Evaluating the Lagrangian •

Electromagnetic fields •

Semiclassical equations of motion •

Berry curvature •

When is the Berry curvature non-zero? •

Berry curvature •

Boltzmann equation •

Dissipation •

Dissipationlessness •

Summary • Transport of electrons in crystals • • • Electric field drives electrons Impurities, phonons scatter them – resistance Collisions taken into account in the Boltzmann equation Drift of electrons between collisions described by wave-packet dynamics Semi-classical equations contain a non-trivial correction due to the Berry curvature This correction gives rise to a Hall conductivity • Dissipation in DC transport • • Associated with entropy production It comes from the longitudinal part of the conductivity The Hall conductivity is NOT associated with dissipation In order to get dissipationless transport • Make the longitudinal conductivity zero • Keep only the Hall conductivity • To date this is ONLY possible in topological materials – following lectures