Lecture 1 Laws of Thermodynamics Thermodynamic state equilibrium

Lecture 1 Laws of Thermodynamics Ø Thermodynamic state - equilibrium Ø Thermodynamic processes Ø Laws of thermodynamics Ø Absolute Temperature Ø Problems 2. 5, 2. 6, 2. 8

Thermodynamic state - equilibrium Ø Thermodynamic intensive coordinates are uniform across the whole system (T, P, ) or across each macroscopic phase (e. g. , water and ice density at the melting point. Ø All thermodynamic coordinates are time independent Ø Mechanical equilibrium, thermal equilibrium and chemical equilibrium

Macroscopic vs. microscopic state Ø Thermodynamic coordinates (T, P, ) define macroscopic state of equilibrium. Ø Microscopic state is defined by atomic positions, and momenta - many microscopic states are consistent with a macroscopic state Ø Statistical mechanics connects microscopic description and detail with macroscopic state via ensemble average

Thermodynamic process change of thermodynamic state Ø Infinitesimal process infinitesimal change of coordinates, e. g. , d. T, d. V, d. P Ø Quasi static process always near equilibrium Ø Adiabatic process no heat Ø Reversible process can be restored to the initial state without charging surroundings

0 th law of thermodynamics Two or more systems in equilibrium do not exhibit heat flow among each other, they are at the same temperature Later we will see that criterion of equilibrium for isolated system, i. e. , const E, V, T is the maximum entropy state d. S(E, V, N) = 0 Allowing only energy exchange between d. S = d. S 1+d. S 2 = 0 two isolated systems From conservation of energy E 1, V 1, N 1 E 2, V 2, N 2

1 st law of thermodynamics - conservation of energy d. E = d. Q-d. W d indicates inexact differential - depends on the integration path In a cycle, E = 0 net Q in = net W out Work and heat are not state functions Energy is a state function d. W = Fdx can be Pd. V, - dl, - it

2 nd law of thermodynamics - entropy For a reversible process d. Q= Td. S Where S is entropy which a state function, and T is an absolute temperature The entropy can by calculated by integrating heat over a reversible path

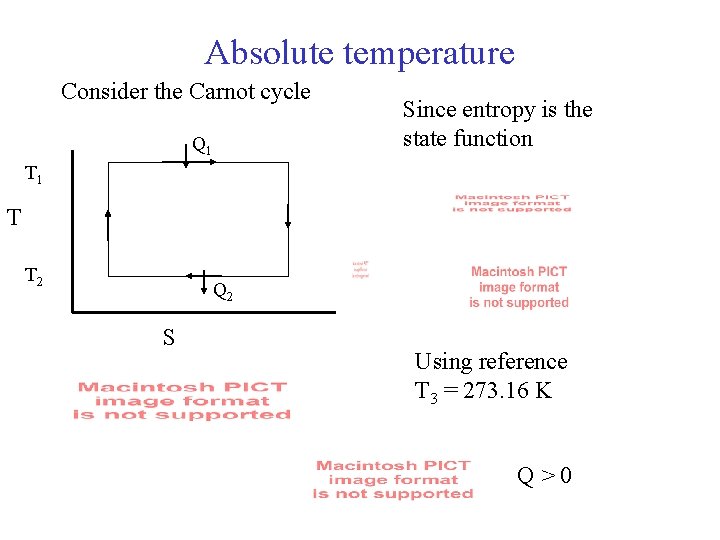
Absolute temperature Consider the Carnot cycle Q 1 Since entropy is the state function T 1 T T 2 Q 2 S Using reference T 3 = 273. 16 K Q>0

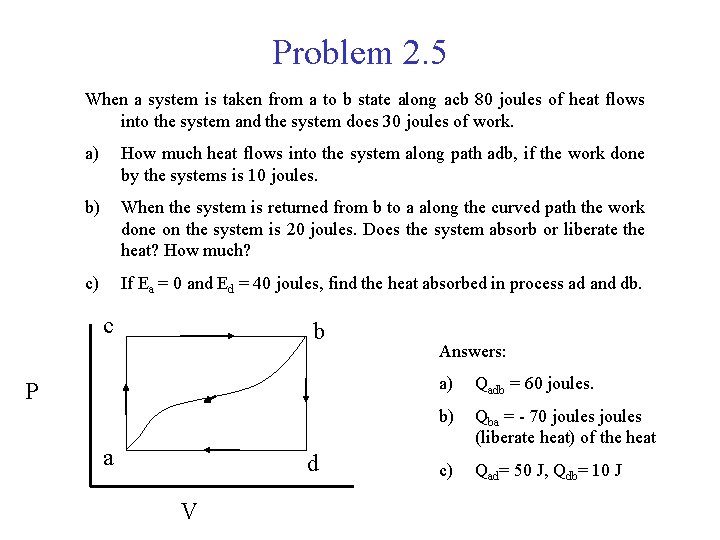
Problem 2. 5 When a system is taken from a to b state along acb 80 joules of heat flows into the system and the system does 30 joules of work. a) How much heat flows into the system along path adb, if the work done by the systems is 10 joules. b) When the system is returned from b to a along the curved path the work done on the system is 20 joules. Does the system absorb or liberate the heat? How much? c) If Ea = 0 and Ed = 40 joules, find the heat absorbed in process ad and db. c b P a d V Answers: a) Qadb = 60 joules. b) Qba = - 70 joules (liberate heat) of the heat c) Qad= 50 J, Qdb= 10 J

Problem 2. 6 A vessel of volume VB contains n moles of gas at high pressure. Connected to the vessel is a capillary tube trough which the gas may slowly leak out into the atmosphere, where P=P 0. Surrounding the vessel and capillary is a water bath, in which is immersed an electric resistor. The gas is allowed to leak slowly trough the capillary into the atmosphere while, at the same time, electrical energy is dissipated in the resistor at such a rate that the temperature of the gas, the vessel, the capillary and the water is kept equal to that of the surrounding air. Show that, after as much gas is leaked as is possible during time , the change of internal energy is where, v 0 = molar volume of gas at P=P 0, = potential on the resistor, and i is the current.

Problem 2. 8 The tension force in a wire is increased quasi statically and isothermally from 1 to 2. If the length, cross-sectional area and isothermal Young’s modulus (Y) remain practically constant, show that the work done by the wire is: