Lecture 1 Course Overview Motivation Fundamental Concepts Cp

Lecture 1. Course Overview, Motivation, Fundamental Concepts Cp. Sc 212: Algorithms and Data Structures (reproduced and adapted with permission from Brian C. Dean) Chad Waters School of Computing Clemson University Fall, 2013

Introductions � Instructor: Chad Waters Bachelors from Winthrop University. Research Interests: Algorithms, Bioinformatics Email: cgwater@clemson. edu Office: Mc. Adams 216 Office Hours: Tuesday, Thursday 1 pm – 3 pm � � � Lab TAs (office hours TBA): Rommel Jalasutram Elham Ebrahimi Blair Durkee � � � 2

Course Overview � This course provides a fun, fast-paced, modern introduction to algorithms and data structures. � We will… Practice using different algorithm design techniques. Improve our analytical skills while learning mathematical tools for algorithm analysis. Learn fundamental algorithms and data structures. Learn the inner workings of some of the algorithms that currently have the most impact in practice. Improve our coding skills. � � � 3

Why Learn Algorithms? . . . � Algorithms are the heart and sole of computing! � Algorithmic computing now plays a key role in nearly everything – proficiency opens many doors. Commerce Science Engineering (Algorithmic) CS Health � Algorithmic prowess differentiates a true “computer Society Arts scientist” from a run-of-the-mill “programmer”, and provides the foundation for a long-term career in computing that can thrive as technology changes. � Algorithms are fun! 4

Programming Algorithmic Problem Solving � “Computer Science is no more about computers than astronomy is about telescopes” – folklore, sometimes attributed to E. Dijkstra. � Programming and software engineering are certainly an important part of most computing projects and careers. � Problem-solving skills and programming skills are different, but re-inforce each-other. � Both are crucial for success as a computing expert. 5

Course Details � Prerequisites C and C++ programming at the level of Cp. Sc 101/102. Enthusiasm, willingness to challenge yourself and ask questions, and a good work ethic! � � � Course Materials No official textbook. Lecture slides (and possibly draft chapters of Dean's book) to be made available throughout the semester. � � 6

Assignments and Grades � Laboratory Exercises (15%) Lab attendance mandatory. � � Homework (35%) Mix of coding and design / analysis questions. Coding exercises graded based primarily on correctness and efficiency, but also readability and elegance. Submit solutions electronically by noon on due date. No late assignments accepted. � � � Midterm (25%) and Final Exam (25%) � No absolute grading scale; appropriate letter grade cutoffs set by instructor at end of semester. 7

Course Conduct � Attendance and Participation Please attend and participate. � � Academic Integrity: Do not cheat or plagiarize! � � Collaboration: Highly encouraged, but all submitted work should be your own. No copying others’ code, or using code from web! � � Feedback: Feel welcome to ask for or give feedback at any time. The instructor always appreciates constructive feedback. � 8

A Good Algorithm (or Data Structure)… � Always terminates and produces correct output. A “close enough” answer is sometimes fine. Some types of randomized algorithms can fail, but only with miniscule probability. � � � Makes efficient use of computational resources. Minimizes running time, memory usage, processors, bandwidth, power consumed, heat produced. � � Is simple to describe, understand, analyze, implement, and debug. 9

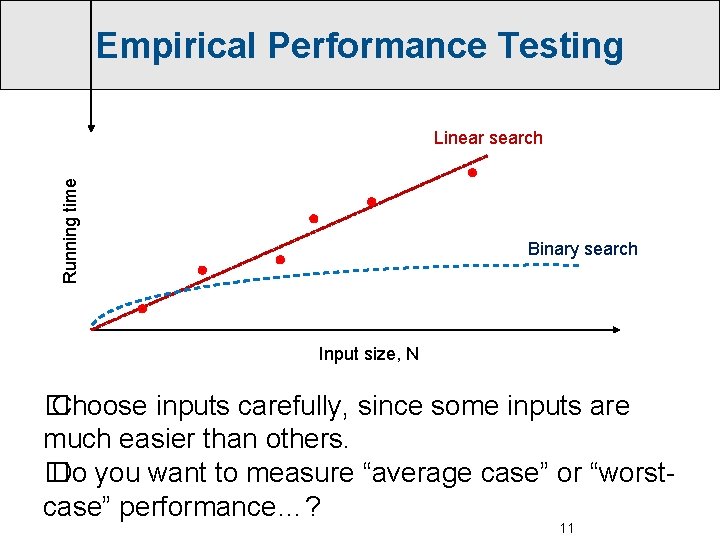
Example: Searching a Sorted Array � Linear search: runs in N “steps” in the worst case. for (i=0; i<N; i++) if (target == A[i]) { found it! } � Binary search: ≤ log 2 N “steps” in worst case. low = 0; high = N-1; while (low <= high) { mid = (low + high) / 2; if (target == A[mid]) { found it! } if (target > A[mid]) low = mid+1; else high = mid-1; } A[0] 10 A[N– 1]

Empirical Performance Testing Running time Linear search Binary search Input size, N � Choose inputs carefully, since some inputs are much easier than others. � Do you want to measure “average case” or “worstcase” performance…? 11

Asymptotic Analysis � Linear search: O(N) time. � Binary search: O(log N) time. � O(f(N)) means “upper-bounded by a constant times f(N) as N grows large”. � Provides an asymptotic upper bound on running time, where constant factors and lower-order terms don’t matter. � Captures what really matters about algorithm performance: how worst-case running time scales with input size. 12

Asymptotic Notation � O() provides an asymptotic upper bound. � Ω() provides an asymptotic lower bound. � Θ() means both a lower and upper bound. (think of these as “≤”, “≥”, and “=”) Usage examples: “The running time of our algorithm is O(n 2). ” “The worst-case running time of our algorithm is Θ(n 2). ” “This algorithm uses Ω(n 2) memory”. “ 17 n 2 – 5 n + 200 = Θ(n 2)” “Consider the polynomial 5 x 10 – 3 x 9 + O(x 8). ” � � � 13

Running Times � We almost always focus on worst case running times. Why? � Common running times: Constant: O(1) Logarithmic: O(log n) Linear: O(n) Polynomial: O(n log n), O(n 2), O(n 3), O(n 100), … Exponential: O(2 n), O(3 n), … Worse than exponential: O(n!), O(nn). � � � � Logs: base doesn’t matter in O(), as long as not in an exponent. By log n we usually mean log 2 n. 14

Fundamental Data Structures A[0] A[N– 1] Arrays NULL head Linked Lists 15

Arrays A[0] A[N– 1] /* Statically defined (size known at compile time) */ int A[100]; int B[100] = {1, 2, 3}; /* Dynamically allocated at run time */ int *C = (int *)malloc(100 * sizeof(int)); int *D = new int[100]; /* A[], C[], and D[] filled with garbage until initialized */ /* Remember pointers can be used as arrays -- e. g. , C[7] */ /* Don’t forget to free memory for C and D… */ free (C); delete [] D; 16

Linked Lists NULL head /* In C, typically use “typedef struct…” */ struct Node { int payload; Node *next; } int list_length(Node *n) { int count = 0; while (n != NULL) { count++; n = n->next; } return count; } � Sometimes we use “doubly” linked lists (pointers to prev and next elements). � Sometimes end of list is marked with a dummy “sentinel” element, instead of a pointer to NULL. � Sometimes we maintain a pointer to the first and last element (to speed up appending to the end). 17

Array and Linked List Performance A[0] A[N– 1] � Retrieve or modify any element in O(1) time. � Insert or delete in middle of list: O(N) time. � Insert or delete from ends: O(1) time Be careful not to run over end of allocated memory Possibly consider using a “circular” array… � � NULL head � Seek to any position in list: O(N) time. � Then insert or delete element: O(1) time. � Insert or delete from ends: O(1) time. 18

Circular Arrays, Queues A[0] back front A[N– 1] back � First-In, First-Out (FIFO). � Could be implemented using linked lists instead… void enqueue(int x) { A[front] = x; front = (front+1) % N; } int dequeue(void) { int result = A[back]; back = (back+1) % N; return result; } 19

Circular Arrays, Queues A[0] back front A[N– 1] back � First-In, First-Out (FIFO). � Could be implemented using linked lists instead… � Example: “cat file | grep algorithm | wc –l” counts the number of lines in file containing “algorithm”. Queues are used to send data from one program to the next along the pipeline. 20

Stacks top A[0] � Last-In, First-Out (LIFO). � Could also be implemented with a linked list. . . void push(int x) { A[top++] = x; } int pop(void) { return A[--top]; }

Stacks top A[0] � Example: A stack is used to store the state of unfinished function calls. For example… void what_does_this_do(int n) { if (n==0) return; printf (“%dn”, n); what_does_this_do(n-1); printf (“%dn”, n); }

Time for a Challenge… (this used to be a popular interview question) � You are given a pointer to the beginning of a linked list. � It either ends by pointing to NULL: NULL or it ends by pointing back into itself, forming a loop: � Goal: Determine as quickly as possible which of these two cases is occurring.

Time for a Challenge… (this used to be a popular interview question) � You are given a pointer to the beginning of a linked list. � It either ends by pointing to NULL: NULL or it ends by pointing back into itself, forming a loop: � Goal: Determine as quickly as possible which of these two cases is occurring. � To make things interesting: You aren’t allowed to modify the list, or to use substantial amounts of extra memory…

“Slow Pointer / Fast Pointer” Tricks Have Surprisingly Many Applications! � Synchronizing parallel processors. � Detecting infinite loops in programs automatically as they run. � Factoring large integers [Pollard].

Parallel Algorithm Example: The “Firing Squad” Problem � N parallel processors hooked together in a line: � Each processor doesn’t know N, and only has a constant number of bits of memory (so it can’t even count to N). � Processors synchronized to a global clock. In each time step, a processor can: Perform some simple calculation. Exchange messages with its neighbors. � � � At some point in time, we give the leftmost processor a “ready!” message. � Sometime in the future, we want all the processors to enter the same state “fire!” all in the same time step.

The “Firing Squad” Problem: Solution � Send messages at speeds 1 x and 3 x. The fast message bounces off the right endpoint and heads back to the left. � They collide at the middle processor in O(N) steps. � The middle processor then pretends to be an endpoint, and sends “Ready!” messages out in both directions. � First and second halves of the array now simultaneously perform the same execution pattern (mirror-imaged)! � Soon, the two halves are divided into 4 ths, then 8 ths, etc. � What is the total running time? . . .