Lecture 1 Ch 1 System of Linear Equation

Lecture 1 Ch 1. System of Linear Equation and Matrices Delivered by: Iksan Bukhori iksan. bukhori@president. ac. id Original Presentation by Filson Maratur Sidjabat Matrices & Vector Spaces 2018

Textbook and Syllabus Textbook: Elementary Linear Algebra. Anton, Howard. 1994. , 7 th ed. , Wiley & Sons, New York Linear Algebra with Applications. Leon J. , Steven. 2006. , 7 th ed. , Pearson Prentice Hall, New Jersey. Any other relevant link and website / e-book, e. g Chapter 1 http: //www. wiley. com/college/mat/anton 170526/resources/ ch 01 app. pdf Syllabus: (tentative) � Chapter 1 – System of Linear Equation and Matrices � Chapter 2 – Determinants � Chapter 3 – Vector in 2 -spaces and 3 -spaces � Chapter 4 – Euclidean Vector Spaces � Chapter 5 – General Vector Spaces

Grade Policy Final Grade = 10% Homework + 15% Quizzes + 35% Midterm Exam + 40% Final Exam+ Extra Points § Homeworks will be given in fairly regular basis. The average of homework grades contributes 10% of final grade. § Homeworks are to be written on A 4 papers, otherwise they will not be graded. § Homeworks must be submitted on time, one day before the schedule of the lecture. Late submission will be penalized by point deduction of – 10·n, where n is the total number of lateness made. § But you can submit homework late without penalty by sending the scanned homework to my email a day before class

Grade Policy § Extra points will be given if you solve a problem in front of the class. You will earn 1, 2, or 3 points. § Make up of quizzes and exams will be held one week after the schedule of the respective quizzes and exams. § To maintain the integrity, the score of a make up quiz or exam, upon discretion, can be multiplied by 0. 9 (the maximum score for a make up is 90). Matrices-Vector Homework 1 Joni 009201700008 21 April 2014 No. 1. Answer: . . . . Heading of Homework Papers (Required)

Lecture Activities § Lectures will be held in the form of Power. Point presentations. § You are expected to write a note along the lectures to record your own conclusions or materials which are not covered by the lecture slides. How to get good grades in this class? • Do the homeworks by yourself • Solve problems in front of the class • Take time to learn at home • Ask questions

System of Linear Equation � Linear equation is an equation where all variables are in the first order of power with no product, roots, logarithmic, or trigonometric form.

System of Linear Equations • a linear equation in n variables: a 1, a 2, a 3, …, an, b: real number a 1: leading coefficient x 1: leading variable n Notes: (1) Linear equations have no products or roots of variables and no variables involved in trigonometric, exponential, or logarithmic functions. (2) Variables appear only to the first power.

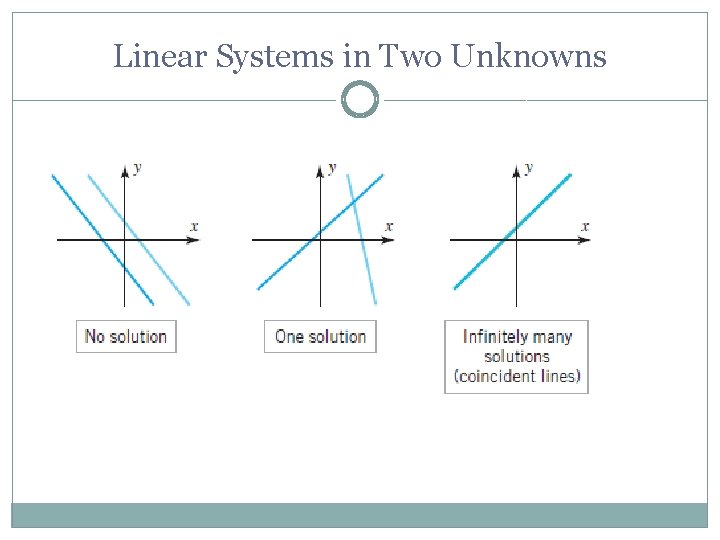
System of Linear Equations • a linear equation in n variables: a 1, a 2, a 3, …, an, b: real number a 1: leading coefficient n Examples: (a) x 1 + 2 x 2 = 5 2 x 1 + 3 x 2 = 8 x 1: leading variable (b) x 1 – x 2 +x 3 = 2 2 x 1 + x 2 - x 3 = 4 (c) x 1 + x 2 = 2 x 1 - x 2 = 1 x 1 =4 If the system has no solution, we say that the system is inconsistent. If the system has at least one solution, we say that it is consistent.

Linear Systems in Two Unknowns

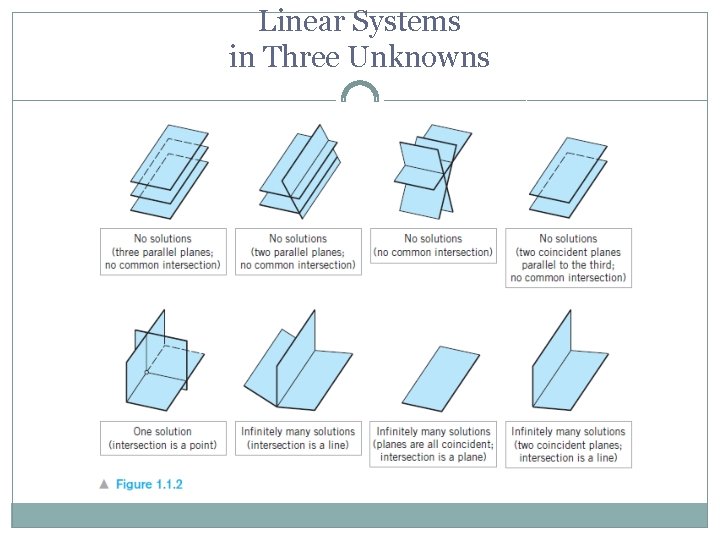
Linear Systems in Three Unknowns

System of Linear Equations • a system of m linear equations in n variables: n Consistent: A system of linear equations has at least one solution. n Inconsistent: A system of linear equations has no solution.

Practice! Find solution for this equation: What method will you use? • Elimination - Substitution • Elementary Row Operation

More Practice! � Elementary Row Operations 1. Interchange two What method will you use? • Elimination - Substitution • Elementary Row Operation rows. 2. Multiply a row by a nonzero real number. 3. Replace a row by its sum with a multiple of another row.

More Practice! � Elementary Row Operations 1. Interchange two What method will you use? • Elimination - Substitution • Elementary Row Operation • Gauss Elimination rows. 2. Multiply a row by a nonzero real number. 3. Replace a row by its sum with a multiple of another row.

Row Echelon Form and Reduced Row Echelon Form (Gauss Jordan Elimination) Row Echelon Form Reduced row Echelon Form � All nonzero rows (rows � The matrix should be in row with at least on nonzero element) are above any rows of all zeroes (all zero rows), if any belong at the bottom of the matrix � The leading coefficient (the first nonzero number from the left, also called the pivot) of a nonzero row is always strictly farther to the right of the leading coefficient of the row above it (some texts add the condition that the leading coefficient must be 1) echelon form � Every leading coefficient is 1 and is the only nonzero entry in its column

Row Echelon Form and Reduced Row Echelon Form (Gauss Jordan Elimination)

Row Echelon Form and Reduced Row Echelon Form (Gauss Jordan Elimination) �If we use only the first five steps, the above procedure produces a row-echelon form and is called Gaussian elimination. �Carrying the procedure through to the sixth step and producing a matrix in reduced row-echelon form is called Gauss–Jordan elimination.

Answer review (1)

Answer review (2)

Answer review (3)

Elimination methods Soal:

If we use only the first five steps, the above procedure produces a rowechelon form and is called Gaussian elimination. Carrying the procedure through to the sixth step and producing a matrix in reduced row-echelon form is called Gauss–Jordan elimination.

Homework 1: System of Linear Equation �