Lecture 1 Analysis and Design Graph Coloring Problems

Lecture 1: – Analysis and Design Graph Coloring Problems Han Jing Complex Systems Research Center, Institute of Systems Science, AMSS hanjing@amss. ac. cn

Outline • What is a Graph Coloring Problem (GCP)? • Intro. to algorithms of solving GCPs • Analysis of one kind of collective behavior: – phase transition of “SAT/UNSAT”, “Easy/hard” • Design of the local rule for agents/nodes: – individual, compartment and the whole

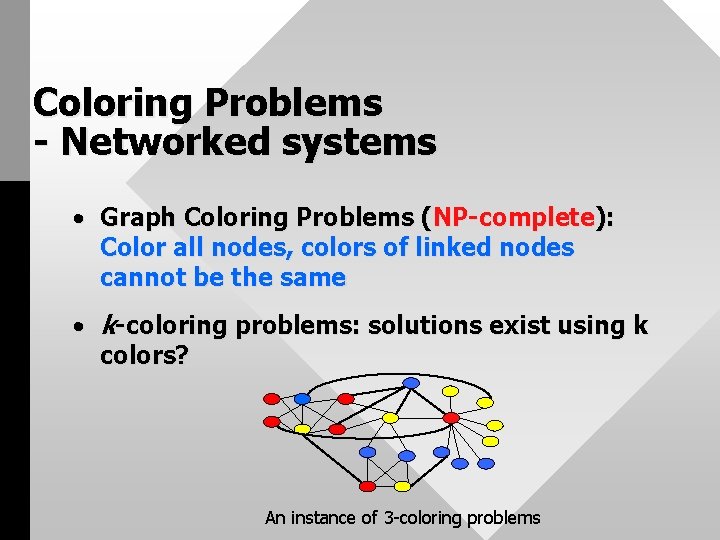
Coloring Problems - Networked systems • Graph Coloring Problems (NP-complete): Color all nodes, colors of linked nodes cannot be the same • k-coloring problems: solutions exist using k colors? An instance of 3 -coloring problems

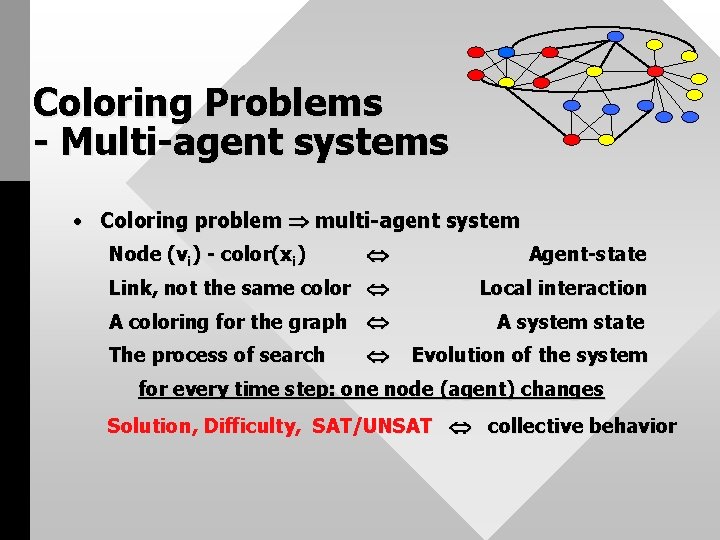
Coloring Problems - Multi-agent systems • Coloring problem multi-agent system Agent-state Link, not the same color Local interaction A coloring for the graph A system state Evolution of the system Node (vi) - color(xi) The process of search for every time step: one node (agent) changes Solution, Difficulty, SAT/UNSAT collective behavior

How we find a solution by using a computer? What are the algorithms?

Search - Universal Technique • Search Style – Systematic Search: assign values to variables sequentially. E. g. : Backtracking, … – Generate & test : a possible configuration of all variables, E. g. : local search (simulated annealing, metropolis algorithm ), Genetic algorithm, AER, hill-climbing, Tabu, Restart, … • How many configurations in a time – Individual-based (Single-copy): Simulated Annealing, Backtracking… – Population-based (Multi-copies): GA, Particle Swarm Optimization… • No one beats all others on all problem instances • This talk only focus on search algorithms in the intersection of Generate &Test and Individual-based: Local Search Note: Related to lectures of Lee ALTENBERG’s on Evolutionary computation

Demo: Uses Local search to solve a k-coloring problem graph: anna, 11 colors, 138 nodes

Three Categories of Research on Collective Behavior 1. Analysis: Given the local rules of the agent, what is the collective behavior of the overall system? Spin Glasses, constraint networks, panic model, network dynamics… 2. Design: Given the desired collective behavior, what are the local rules for agents? Swarm Intelligence, decentralized control 3. Control: Given the local rule of the agent, how we control the collective behavior? Soft Control

Analysis: What kinds of collective behavior occur in Coloring problems? How to predict? Note: Just want to talk a little bit about: • phase transition of ‘SAT/UNSAT’, ‘easy-hard’ in the coloring problem; • point out the relationship between coloring problems and statistical physics • Zhou Hanjun’s lecture will focus on Statistical physics and the combinatorial optimization problem.

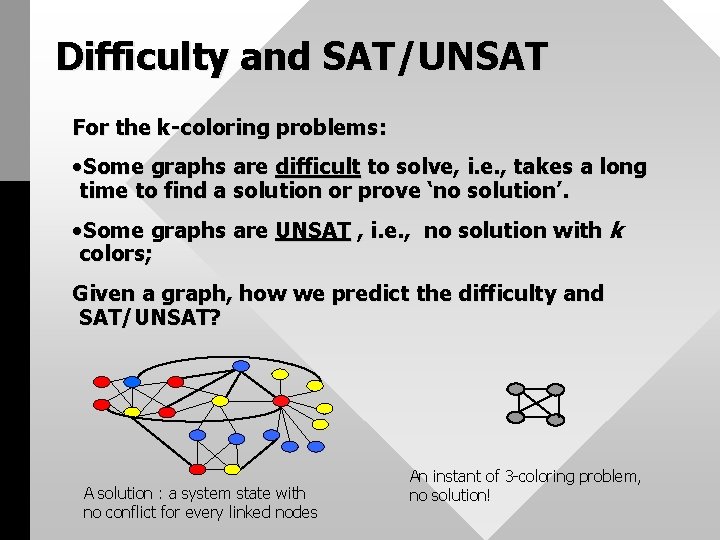
Difficulty and SAT/UNSAT For the k-coloring problems: • Some graphs are difficult to solve, i. e. , takes a long time to find a solution or prove ‘no solution’. • Some graphs are UNSAT , i. e. , no solution with k colors; Given a graph, how we predict the difficulty and SAT/UNSAT? A solution : a system state with no conflict for every linked nodes An instant of 3 -coloring problem, no solution!

Phase transition of SAT/UNSAT, difficult/easy • Random GN, p – N, number of nodes – P, probability of a link for a pair of nodes obey Poisson Distribution. – = p N, avg. degree – Allow number of colors: k k c 3 4. 69 4 8. 90 5 13. 69 … SAT% cost 4. 69 The case of k=3, random graphs w c, critical point of SAT/UNSAT usually, at this point the graph instances are difficult to solve w < c, possible ‘SAT’, easy to solve w > c, possible ‘UNSAT’, easy to solve

How they got these values? k k 3 4. 69 4 8. 90 5 13. 69

Coloring Problem vs. Thermodynamic System Combinatorial P Thermo. S Variable (node) Particle Value assignment (color) Status of particle Constraint (link) Interaction A possible (coloring) configuration A microscopic state Evaluation function, (objective function) Energy (Hamiltonian) Solutions Ground states Local search Evolution Note: Soon I will talk about the Evaluation Function.

Statistical Physics Statistical physics is about systems composed of many parts. • Traditional examples: – Gas, liquid, solid – atom or molecule; – Metal, semiconductor- electron; – Quantum fields - quantum，electromagnetic fields – photons • Complex systems examples: – – – Ecosystem- species Social system- individuals Computer network- Computer Market - agent Bird flock – bird, ant colony - ant Combinatorial optimization – variable *Most of this slide is from Mark Newman’s lecture in Budapest CSSS-2001.

The theory Spin Glasses (combinatorial optimization problems, Ising Model) – Gibbs Entropy Boltzmann distribution Partition function Z: Z(0)=number of ground states (solutions) Z(0)>0 SAT, Z(0)=0 UNSAT – Mean-field (Replica Symmetry, Cavity Methods) Note: Zhou Haijun’s lecture will talk about Cavity methods. Note: For details, see Cris Moore’s lecture on ‘Phase Transitions in Physics and Computer Science’ in CSSS 07 -Santafe.

Reference for Spin glasses • Mark Newman 2001 summer school lecture http: //www. santafe. edu/~mark/budapest 01/ • Theory of Spin Glasses And Neural Networks. • Spin Glass Theory and Beyond. • An Introduction to theory of spin glasses. I. Kondor. Sci. Prog. , Oxf. (1987) 71, 145 -180. • K-SAT: Nature, Vol 400, July 1999, p 133 -137 • Survey Propagation: Science, Vol 297, Aug. 2002, p 812 -815, p 784 -785.

Now, go to the main theme of today: Design Individual, Compartment and the Whole

Individual, Compartment and the Whole Han Jing Complex Systems Research Center, Institute of Systems Science AMSS, CAS July 22, 2004 at CSSS-04, Qingdao July 22, 2005 at CSSS-05, Beijing July 20, 2006 at CSSS-06, Beijing July 24, 2007 at CSSS-07, Beijing July 10, 2008 at CSSS=08. Beijing

Three Categories of Research on Collective Behavior 1. Given the local rules of the agent, what is the collective behavior of the overall system? Spin Glasses, constraint networks, panic model, network dynamics, 2. Given the desired collective behavior, what are the local rules for agents? Swarm Intelligence, decentralized control 3. Given the local rule of the agent, how we control the collective behavior? Soft Control

Story -- The Programmer was thinking very hard about how to design the local rule for each agent (node) to solve the coloring problems. -- Suddenly, he saw a book <Game theory>. He opened it and read. -- He got new ideas …

One kind of Evolution Note: Lee ALTENBERG will talk about Evolutionary computation next week, which focus on population-based style algorithm. This lecture focus on the other style, only one individual configuration.

Evolution • Evolution: the process of going from initial system state to some system state. • Direction of evolution: Evaluation Functions ？

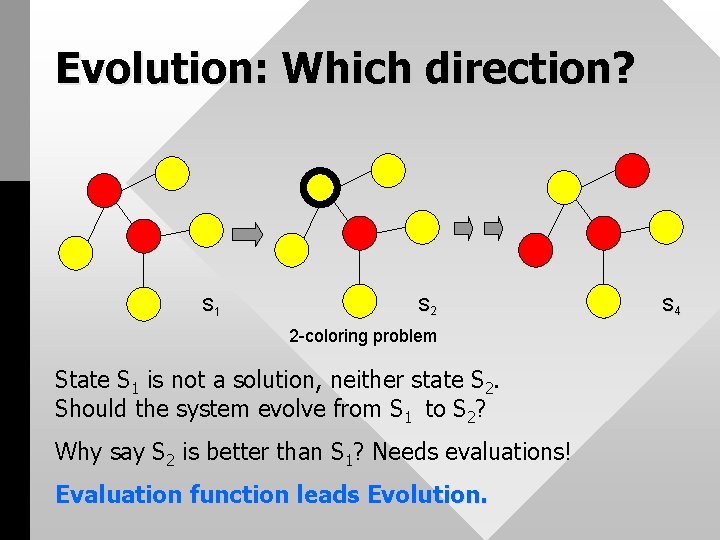
Evolution: Which direction? S 1 S 2 2 -coloring problem State S 1 is not a solution, neither state S 2. Should the system evolve from S 1 to S 2? Why say S 2 is better than S 1? Needs evaluations! Evaluation function leads Evolution. S 4

Evaluation Function • An Evaluation Function (EF) f: S→ , S : state (configuration) space • Fitness function, Cost function, Penalty function, Objective function, Energy function, Hamiltonian… • Evolution: optimizes the EF Note: In ALTENBERG’s lecture, evaluation function is called ‘objective function’ and ‘fitness function’

Examples of Evaluation Functions – Penalty function of k-Coloring Problems e. g. , f=∑i∑j (xi, xj), f =∑i∑j (xi, xj)didj – Hamiltonian in spin glasses e. g. , E = - J(i-1)isi-1 si – Cost function in a statistical learning * (xi, xj)=1 when vi links to vj and xi=xj, otherwise =0. algorithm Q(f)= wij(fi/pairs. Di f=∑i∑j (xi, xj 2)) counts the total number of conflicting -fj/ Dj) + (fi-yi)2) – Fitness function of NK model for biological evolution: W =1/N wj Note: But in some systems, there is no explicit evaluation function.

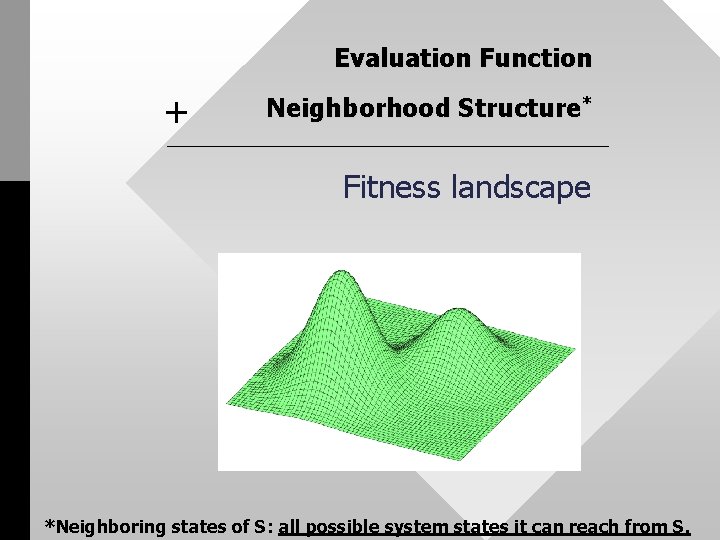
Evaluation Function + Neighborhood Structure* Fitness landscape *Neighboring states of S: all possible system states it can reach from S.

Neighborhood of Local search • Sequential For every time step, only one agent can make changes (evolves) v 2 changes v 3 changes v 1 changes v 4 changes 1 2 3 4 v 2 changes 5 time

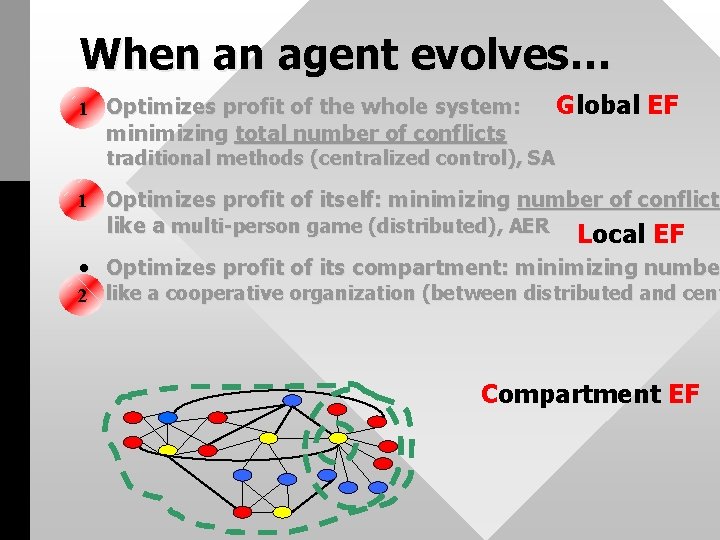
When an agent evolves… 1 • Optimizes profit of the whole system: minimizing total number of conflicts Global EF traditional methods (centralized control), SA 1 • Optimizes profit of itself: minimizing number of conflicts conflict like a multi-person game (distributed), AER Local EF • Optimizes profit of its compartment: minimizing number numbe 2 like a cooperative organization (between distributed and cent Compartment EF

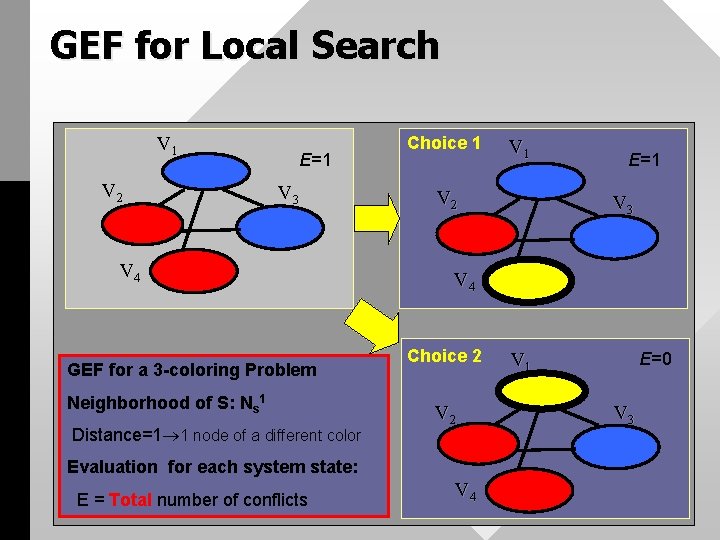
GEF for Local Search V 1 V 2 E=1 V 3 V 4 GEF for a 3 -coloring Problem Neighborhood of S: Ns 1 Distance=1 1 node of a different color Choice 1 V 2 E=1 V 3 V 4 Choice 2 V 2 Evaluation for each system state: E = Total number of conflicts V 1 V 4 V 1 E=0 V 3

GEF: Global Goal • Evaluates how good a global system state is • GEF: Knows all agents’ states (color) • Centralized Control • k-Coloring Problem: f. G=∑i∑j (xi, xj) • Stable states: local optima of the GEF

LEF (Alife&AER, EO)

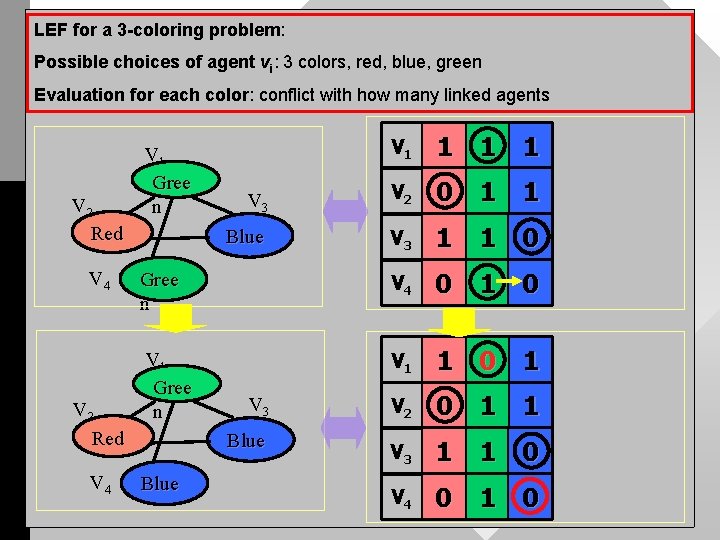
LEF for a 3 -coloring problem: Possible choices of agent vi: 3 colors, red, blue, green LEF (Alife&AER, EO) Evaluation for each color: conflict with how many linked agents V 2 Red V 4 V 1 1 V 3 V 2 0 1 1 Blue V 3 1 1 0 Gree n V 4 0 1 0 V 1 Gree n V 1 1 0 1 V 3 V 2 0 1 1 Blue V 3 1 1 0 V 4 0 1 0 V 1 Gree n Blue

LEF: Individual Goal • Evaluates how good a single agent state is • Use local information to guide agent Only knows its linked agents’ state (color) • Distributed Control • Each agent try to minimize – k-Coloring Problem fi=∑j (xi, xj) • Stable states: Nash equilibria of the LEF

Why LEF? • LEF leads to global goal: design the local rule for agents, and reach the expected collective behavior (reach to solution state) • Distributed optimization methods – Parallel Computing – More feasible in some cases Cannot satisfy all agents If the local optimum of GEF is not Nash Equilibrium of the LEF, the solution is not stable. • LEF can efficiently find the global solution for the coloring problems ?

The Essential Relationship between LEF and GEF • Consistency between LEF and GEF • The Consistency Theorem (Nash Equilibrium and local optimum) • A sufficient condition for consistency (Symmetrical Interaction) • The existence of consistent GEF (cycling behavior)

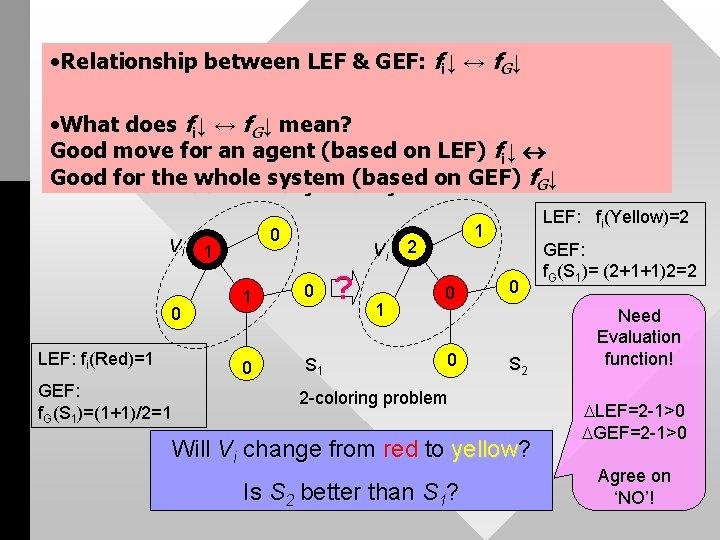
• Relationship between LEF & GEF: fi↓ ↔ f. G↓ An LEF agrees with a GEF • What does fi↓ ↔ f. G↓ mean? • Good LEFmove fi=∑jfor (xan agent (based on LEF) fi↓ i, x j); Good the system GEFfor f G= ∑iwhole fi/2=∑ i∑j (x(based i, xj)/2 on GEF) f. G↓ Vi 0 LEF: fi(Red)=1 GEF: f. G(S 1)=(1+1)/2=1 0 1 Vi 1 0 0 S 1 ? 1 LEF: fi(Yellow)=2 1 2 0 0 0 S 2 2 -coloring problem Will Vi change from red to yellow? Is S 2 better than S 1? GEF: f. G(S 1)= (2+1+1)2=2 Need Evaluation function! LEF=2 -1>0 GEF=2 -1>0 Agree on ‘NO’!

The Consistency Theorem • Consistency definition: for all S and S’ Ns 1: Sgn(f. G(S’)-f. G (S)) = Sgn(fi(S’)-fi(S)) • Stable states of a GEF are the Local Optima. S is a Local Optimum if S’ Ns 1, f. G(S) f. G (S’) • Stable states of an LEF are the Nash Equilibria. S=<s 1, s 2, …, sn> is an Nash Equilibrium if i 1. . n, si’ Di, fi(S, si) fi (S, si’) • Consistency Theorem: An LEF is consistent with a GEF {Nash Equilibria of the LEF }= {Local optima of the GEF} • So, – that is why consistent LEF works

Questions • Given a LEF, is there a GEF that is consistent with the LEF? Not always LEF: {fi}, how about GEF=∑fi? • Given a GEF, is there a LEF that is consistent with the GEF? Are all GEFs decomposable?

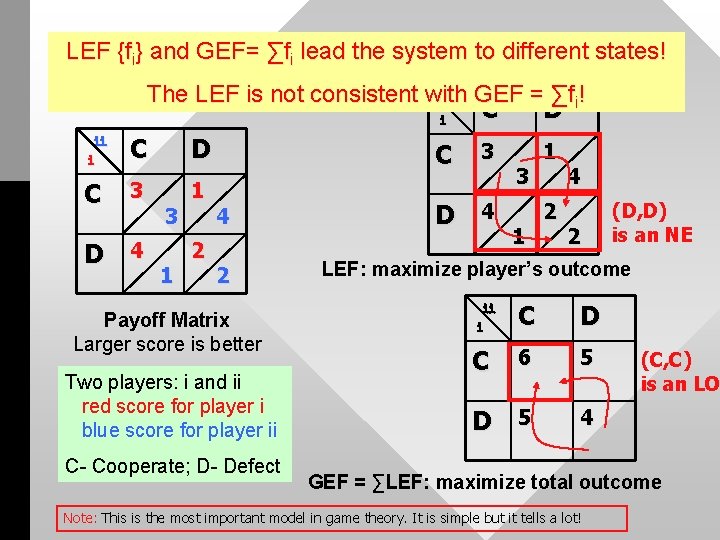
LEF {fi} and GEF= ∑fi lead the system to different states! Prisoner’s Dilemma The LEF is not consistent with GEF = ∑f ! The LEF is not consistent with ⅱ GEF = ∑fi ! ⅱ ⅰ C D C 3 1 D 4 3 1 2 4 2 Payoff Matrix Larger score is better Two players: i and ii red score for player i blue score for player ii C- Cooperate; D- Defect ⅰ C D C 3 1 3 D 4 4 2 (D, D) is an NE 1 2 LEF: maximize player’s outcome ⅱ ⅰ C D C 6 5 D 5 4 (C, C) is an LO GEF = ∑LEF: maximize total outcome Note: This is the most important model in game theory. It is simple but it tells a lot!

How can a LEF be consistent? • Consider the following form of evaluation function: h(ai) external field; gij(ai, aj) interaction – LEF: fi= h(xi)+ ∑jgij(xi , xj) – GEF=∑LEF: f. G=∑ih(xi)+ ∑i, jgij(xi , xj) >0 and >maxi{|h(Xi)|} • Symmetrical interaction: if gij(xi , xj) = gji(xj , xi) The LEF is consistent with GEF=∑LEF Note: ‘external field’ is a term in statistical physics.

They are all symmetrical interactions! So the LEF Evolution and Evaluation Function and LEF are consistent • Evolution: optimizing a function – Penalty function of k-Coloring Problems (eg. f=∑i∑j (xi, xj)) (eg. f = -∑i=1, k|Ci|2 +n∑i∑j (xi, xj) for finding minimal colors) – Hamiltonian in spin glasses (eg. E = - J(i-1)isi-1 si) – Cost function in statistical learning ( eg. Q(f)= wij(fi/ Di-fj/ Dj)2+ (fiyi)2) – NK model for biological evolution (W =1/N wj) LEF: fi=∑j (xi, xj) LEF: fi=-J(i-1) (xi, xj) LEF: Qi(f)= wij(fi/ Di-fj/ Dj)2+ (fi-yi)2 LEF: Wi =1/N j Ciwj

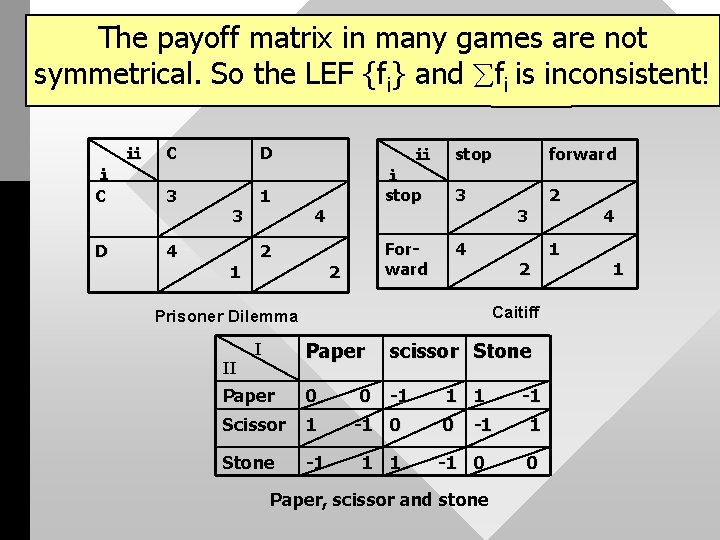
The payoff matrix in many games are not symmetrical. So the LEF {fi} and fi is inconsistent! ⅱ C ⅰ C 3 D 4 D 3 1 1 ⅱ ⅰ stop 4 2 Forward 2 stop forward 3 2 3 4 2 Caitiff Prisoner Dilemma Paper scissor Stone Paper 0 0 -1 Scissor 1 -1 0 Stone -1 1 1 II I 1 1 -1 0 -1 1 -1 0 0 Paper, scissor and stone 1 4 1

Asymmetrical Interaction in Coloring Problems • Symmetrical: fi= j (xi , xj); • Considering degree of nodes: the LEF fi= j (xi , xj) dj the GEF f. G= i j (xi , xj) dj Vi • Better performance in finding solutions in some instances! 1 3

Inconsistency: the local optimum is not a Nash equilibrium! • fi= j (xi , xj) dj ; f. G= i j (xi , xj) dj • An LEF is not consistent with a GEF in some networks. 1 Vi 1 33 3 LEF 3 Vi LEF Vi GEF S 2 S 1 LO, but not NE 2 -coloring problem LEF fi(‘R’) = 0 + 1 3 = 3 LEF fi(‘Y’) = 1 1 + 0 =2 LEF = 2 -3 = -1 < 0 S 1 S 2 S 3 S 4, S 1 is not a NE. GEF f. G(S 1) = 3 + 3 = 6 GEF f. G(S 2) = 2+3+3=8, GEF = 8 – 6 = 2 > 0 S 1 is a Local Optimum! S 4

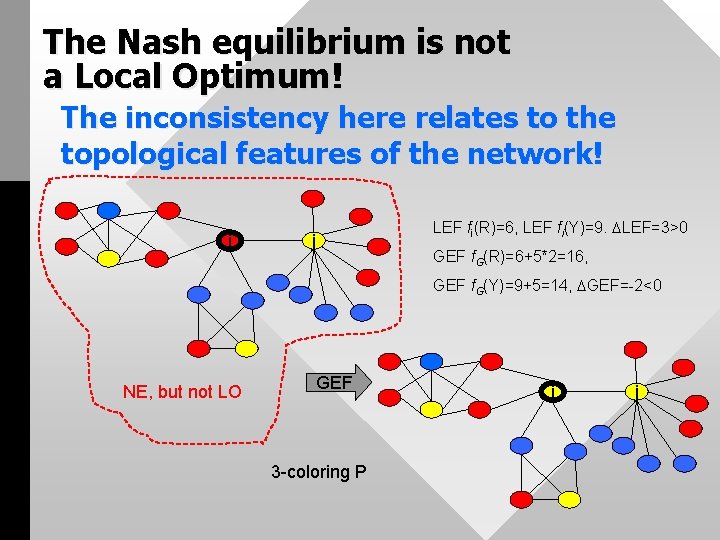
The Nash equilibrium is not a Local Optimum! The inconsistency here relates to the topological features of the network! i LEF fi(R)=6, LEF fi(Y)=9. LEF=3>0 j GEF f. G(R)=6+5*2=16, GEF f. G(Y)=9+5=14, GEF=-2<0 NE, but not LO GEF 3 -coloring P i j

Questions Not always • Given a LEF, is there a GEF that can be consistent with the LEF?

The Existence of Consistent GEF • Limited and discrete systems • (Informal) If the system uses LEF to evolve (deterministic greedy), it always reaches to a Nash Equilibrium (no “cycle”), there exists a consistent GEF (at least it is a consistent enumeration). <described by the partial order relationship> • “symmetrical interaction” is not the necessary condition for consistency LEF fi= j (xi , xj) dj； GEF f. G= i j (xi , xj) dj di ⅱ A ⅰ A -1 B 1 -1 -1 1 Zero-sum game (max. )

2 Compartment • Hierarchy in network • Compartment in food web • Community in Social network • Organization in Economics • Boundary • Combinatorial Problems？ <Nature> Vol. 426, p 284. Note: Now about network … Not until in CSSS-01 did I begin to have interest in networks, even though I had been working on the graph coloring problem-- a network problem for more than a year at that time.

Why Compartment in Coloring Problems? • Starting point: How to remove Local optima? • Discovered hierarchies in networks

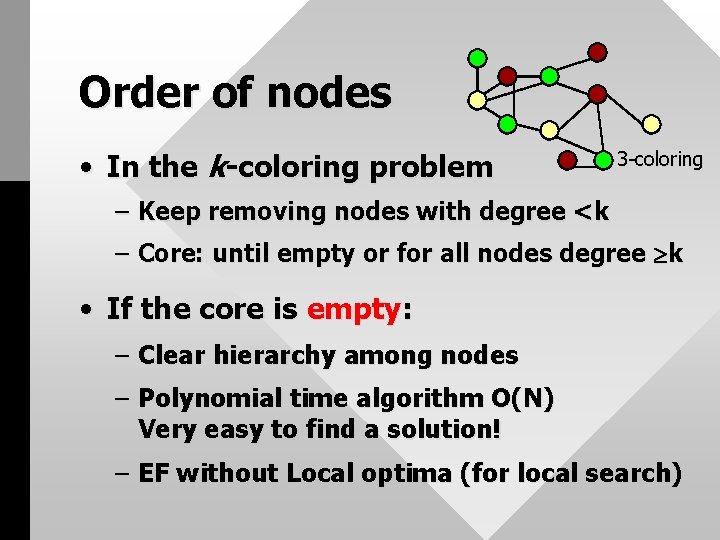
Order of nodes • In the k-coloring problem 3 -coloring – Keep removing nodes with degree <k – Core: until empty or for all nodes degree k • If the core is empty: – Clear hierarchy among nodes – Polynomial time algorithm O(N) Very easy to find a solution! – EF without Local optima (for local search)

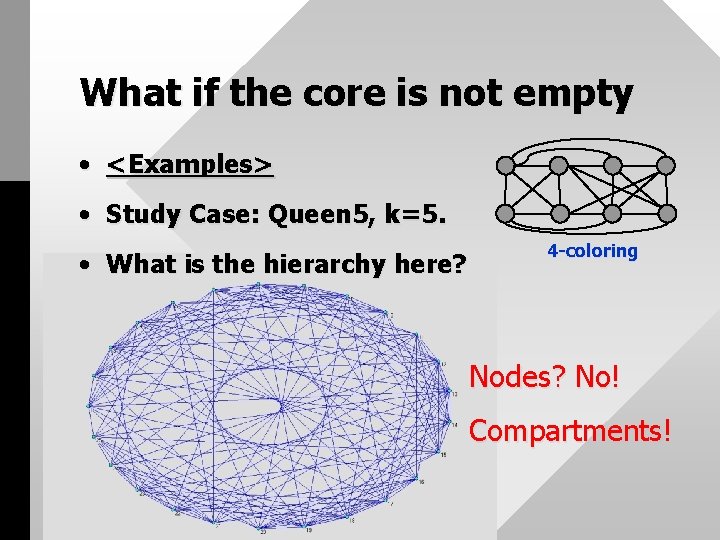
What if the core is not empty • <Examples> • Study Case: Queen 5, k=5. • What is the hierarchy here? 4 -coloring Nodes? No! Compartments!

Review • Networked multi-agent systems – Study case: coloring problem (discrete, limited) • LEF and GEF Definition of Consistency Theorem A sufficient condition – symmetrical interaction Existence of Consistent GEF • CEF (between LEF and GEF) – Order of individual, no backtracking systematic search and local optimum – Hierarchy of compartments, limited backtracking …

Related Papers • From ALIFE Agents to a Kindom of N Queens. Han Jing, Liu, Jiming, and Qingsheng Cai, in Jiming Liu and Ning Zhong (Eds. ), Intelligent Agent Technology: Systems, Methodologies, and Tools , page 110 -120, The World Scientific Publishing Co. Pte, Ltd. , Nov. 1999. • Multi-agent oriented constraint satisfaction. Jiming Liu, Han Jing, Yuan Y. Tang. Artificial Intelligence 136(1): 101 -144, 2002 。 • Emergence from Local Evaluation Function. Han Jing, Cai Qingsheng. Journal of Systems Science and Complexity, Vol. 16 Number 3, pp 372 -390, 2003. • Local Evaluation Functions and Global Evaluation Functions for Computational Evolution. Han Jing. 2003. Complex Systems. Volume 15, Issue 4 (c) 2005, pages 307 - 347 (Santa Fe Institute Working Paper 03 -09 -048) • Consistency between distributed and Centralized Search Algorithms. Han Jing. (Submitted) • A Case Study of the Hidden Hierarchy in the Constraint Networks. (Working paper)

Thank you! Welcome for comments: hanjing@amss. ac. cn